Моделирование диффузионного переноса твердого вещества, растворенного в жидкой среде
Аннотация
Исследована проблема упрощения анализа диффузионного переноса твердого вещества в жидкой среде с учетом факторов в виде переменной скорости движения и переменной скорости распада примеси. Проведен полный анализ критериев подобия диффузионного переноса твердого вещества в подвижной вязкой жидкой среде с учетом силы тяжести, процесса распада, временного фактора и давления в потоке жидкости. Результаты работы применимы в сопоставлении, анализе данных натурного и лабораторного эксперимента для решения ряда задач охраны труда и безопасности в чрезвычайных ситуациях.
Ключевые слова: диффузия, перенос, примесь, поток, распад вещества, безопасность в чрезвычайных ситуацияхКлючевые слова:
05.26.02 - Безопасность в чрезвычайных ситуациях (по отраслям)
В натурных наблюдениях процесса диффузионного процесса переноса растворенного твердого вещества ситуация осложняется тем, что жидкость растворителя имеет некоторую гидродинамическую скорость движения. Например, жидкость морской, океанической или озерной воды обладает такой подвижностью в широких пределах. В [1] обсуждается постановка важной задачи экологии и геофизики о распространении радиоизотопной примеси в соленой морской воде с учетом процесса распада радиоизотопа. В реальных условиях скорость жидкости переменная величина, что не учитывается авторами [1]. В предлагаемой работе проводится обобщение результатов [1] на случай, когда скорость движения жидкости растворителя и постоянная распада являются переменными величинами, зависящими от времени. Такое обобщение позволяет более полно изучать наиболее сложные задачи безопасности технологических процессов, а также адекватные по отношению к практике задачи о последствиях техногенных катастроф и о процессах геофизического масштаба.
В первой части предлагаемой работы проводятся преобразования системы дифференциальных уравнений, позволяющие свести рассматриваемую проблему к решению двух несвязанных дифференциальных уравнений теплопроводности стандартного вида. Во второй части работы проводится анализ критериев подобия при наличии других физических процессов, осложняющих наблюдение диффузии вещества (учитываются силы вязкости и тяжести, силы давления в потоке текущей жидкости. процессы распада).
1. Преобразования системы уравнений диффузии радиоизотопа и солености жидкости
Пусть ![]() -концентрация радиоизотопа в воде, а
-концентрация радиоизотопа в воде, а ![]() -соленость воды. Уравнения турбулентной диффузии радиоизотопа и солей с учетом скорости течения воды
-соленость воды. Уравнения турбулентной диффузии радиоизотопа и солей с учетом скорости течения воды ![]() имеют следующий вид
имеют следующий вид ![]()
(1)![]()
если перенос веществ и течение происходят вдоль одной и той же линии[1]. В данном случае эта линия параллельна оси ![]() . В системе уравнений
. В системе уравнений ![]() −коэффициент турбулентной диффузии,
−коэффициент турбулентной диффузии, ![]() − постоянная распада. В отсутствии процесса диффузии и потока жидкости радиоизотоп распадается в ней по закону
− постоянная распада. В отсутствии процесса диффузии и потока жидкости радиоизотоп распадается в ней по закону![]()
При постоянном значении коэффициента распада концентрация изотопа падает с течением времени по экспоненциальному соотношению![]()
При наличии скорости потока и диффузии зависимость становится сложнее, позволяя решать разные задачи эксперимента. Следует отличать диффузию и смешение жидкостей. При постановке эксперимента следует исключить конвекцию. В натурных условиях может присутствовать скорость течения жидкости. Например, пусть из данных наблюдений определены: концентрация радиоизотопа, соленость и скорость потока в виде функций времени ![]() . Тогда исходная система дифференциальных уравнений позволяет найти коэффициент турбулентной диффузии жидкости
. Тогда исходная система дифференциальных уравнений позволяет найти коэффициент турбулентной диффузии жидкости ![]() и одновременно постоянную распада радиоизотопа
и одновременно постоянную распада радиоизотопа ![]() .
.
Коэффициент распада может быть переменной величиной. Обобщим постановку задачи [1] на случай переменного коэффициента распада изотопа, полагая, что он является функцией одной переменной - времени ![]() . Пусть функция
. Пусть функция ![]() дифференцируема по переменной
дифференцируема по переменной ![]() и интегрируема по переменной
и интегрируема по переменной ![]() в несобственном смысле. Данное предположение упрощает только расчет. Проведем подстановку в первом уравнении исходной системы дифференциальных уравнений (1) согласно формуле
в несобственном смысле. Данное предположение упрощает только расчет. Проведем подстановку в первом уравнении исходной системы дифференциальных уравнений (1) согласно формуле ![]()
![]()
Новая неизвестная функция ![]() удовлетворяет уравнению теплопроводности, которое учитывает наличие некоторой не нулевой скорости течения жидкости в процессе переноса тепловой энергии в среде
удовлетворяет уравнению теплопроводности, которое учитывает наличие некоторой не нулевой скорости течения жидкости в процессе переноса тепловой энергии в среде![]() . (2)
. (2)
При выбранной форме подстановки новая неизвестная функция удовлетворяет начальному условию в заданный произвольный момент времени ![]() согласно следующему интегральному соотношению
согласно следующему интегральному соотношению![]()
Теперь уравнения для солености и новой неизвестной функции, которая имеет также размерность солености, принимают совершенно одинаковый внешний вид. Продолжим далее преобразование системы уравнений, перейдем в подвижную систему координат, считая, что скорость потока переменна по времени, но не зависит от переменной ![]() , т.е. скорость потока выражается функцией времени
, т.е. скорость потока выражается функцией времени ![]() .
.
Новые переменные ![]() и
и ![]() выразим с помощью старых переменных нашей задачи
выразим с помощью старых переменных нашей задачи ![]() , применяя преобразование, учитывающее значение переменной скорости движения частиц среды
, применяя преобразование, учитывающее значение переменной скорости движения частиц среды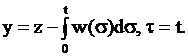 (3)
(3)
Из полученных формул (3) преобразование Галилея, вытекает в виде частного случая для постоянной скорости течения. Частные производные первого порядка по старым переменным от неизвестной функции ![]() равны
равны 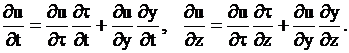
Найдем вторые множители каждого слагаемого правых частей формул. При расчете производной по времени от новой координаты воспользуемся формулой производной от интеграла с переменным верхним пределом. В результате вычислений имеем в итоге следующие два дифференциальных соотношения 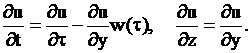 (4)
(4)
Подставим формулы частных производных от функции ![]() вида (4) в систему двух дифференциальных уравнений (1).
вида (4) в систему двух дифференциальных уравнений (1).
После второго преобразования находим, что система несвязанных уравнений принимает стандартный вид 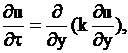
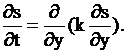
В уравнениях координата ![]() определяет собой подвижную систему координат, относительно которой жидкость неподвижна. Преобразования свели решение исходной задачи к применению процедуры одного типа, что значительно упрощает проведение расчетов и обработку данных натурных и других наблюдений.
определяет собой подвижную систему координат, относительно которой жидкость неподвижна. Преобразования свели решение исходной задачи к применению процедуры одного типа, что значительно упрощает проведение расчетов и обработку данных натурных и других наблюдений.
2. Подобие диффузии полей концентрации твердого вещества в вязкой тяжелой жидкости
Рассмотрим подобие диффузии полей концентраций вещества в жидкости с позиций гидродинамики, т.к. процессы переноса происходят при наличии течения жидкости. Введем необходимые критерии подобия, соответствующие рассматриваемой постановке задачи, согласно обозначениям и соотношениям [1] −[5].
Критерии Рейнольдса -![]() , Фруда -
, Фруда -![]() , Эйлера-
, Эйлера-![]() , Дамкеллера-
, Дамкеллера-![]() находятся в виде формул
находятся в виде формул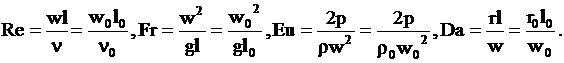 (5)
(5)
Система уравнений подобия (5) решается при предположении, что при переходе к модельной ситуации (отмеченной индексом![]() ) размерные величины в виде ускорения свободного падения
) размерные величины в виде ускорения свободного падения ![]() и давления в жидкости
и давления в жидкости ![]() не меняются. Величина
не меняются. Величина ![]() остается практически постоянной на земной поверхности. В качестве давления
остается практически постоянной на земной поверхности. В качестве давления ![]() в слое жидкости выбираем атмосферное давление для сравнения его с давлением движущейся жидкости. Введем величину количества вещества
в слое жидкости выбираем атмосферное давление для сравнения его с давлением движущейся жидкости. Введем величину количества вещества ![]() , которое распадается в единицу времени в единице объёма жидкого растворителя этого вещества с помощью алгебраического соотношения
, которое распадается в единицу времени в единице объёма жидкого растворителя этого вещества с помощью алгебраического соотношения![]()
Критерий химического подобия Дамкеллера ![]() из [1] может быть записан в несколько более общем виде, который уже не связан здесь непосредственно с какой-то конкретной моделью распада вещества
из [1] может быть записан в несколько более общем виде, который уже не связан здесь непосредственно с какой-то конкретной моделью распада вещества ![]() .
.
Для сохранения химического подобия увеличение концентрации требуется и увеличение скорости распада в единице объёма ![]() Скорость распада вещества может зависеть и нелинейным образом от концентрации вещества. Кроме того, величина
Скорость распада вещества может зависеть и нелинейным образом от концентрации вещества. Кроме того, величина ![]() может описывать выделение и появление некоторого количества вещества в жидкой среде за счет химических процессов или растворения. В случае процесса распада вещества в растворе величина
может описывать выделение и появление некоторого количества вещества в жидкой среде за счет химических процессов или растворения. В случае процесса распада вещества в растворе величина ![]() входит со знаком минус в дифференциальное уравнение расчета концентрации. В другом случае, а именно при наблюдении процесса выделения вещества в раствор, величина скорости выделения
входит со знаком минус в дифференциальное уравнение расчета концентрации. В другом случае, а именно при наблюдении процесса выделения вещества в раствор, величина скорости выделения ![]() в единице объема входит уже со знаком плюс в дифференциальное уравнение расчета концентрации. Второй процесс описывает накопление вещества в растворе. Диффузия препятствует процессу повышения концентрации твердого вещества в растворе в любом рассматриваемом случае переноса твердого вещества в жидкой среде. Для коэффициента диффузии
в единице объема входит уже со знаком плюс в дифференциальное уравнение расчета концентрации. Второй процесс описывает накопление вещества в растворе. Диффузия препятствует процессу повышения концентрации твердого вещества в растворе в любом рассматриваемом случае переноса твердого вещества в жидкой среде. Для коэффициента диффузии ![]() введем критерий подобия, учитывая, что размерности коэффициента диффузии и кинематического коэффициента вязкости
введем критерий подобия, учитывая, что размерности коэффициента диффузии и кинематического коэффициента вязкости ![]() равны
равны
друг другу ![]()
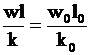 .
.
Полученный критерий подобия позволяет учитывать взаимное влияние двух процессов: диффузии и течения в жидкости. Преобразуем критерий подобия для диффузионного процесса в подвижной жидкости к другому более и удобному виду для сопоставлений
![]() ,
, ![]() . (6)
. (6)
Безразмерная величина – число Шмидта ![]() равно отношению интенсивностей двух процессов : диффузии импульса и диффузии вещества в неподвижной жидкости. Подвижность жидкости в данном критерии подобия учитывается мультипликативным образом с помощью безразмерного числа Рейнольдса
равно отношению интенсивностей двух процессов : диффузии импульса и диффузии вещества в неподвижной жидкости. Подвижность жидкости в данном критерии подобия учитывается мультипликативным образом с помощью безразмерного числа Рейнольдса ![]() .
.
3. Анализ критериев подобия диффузии для полей концентрации твердого вещества в подвижной жидкости
Выше приведены пять критериев подобия для наблюдения процессов диффузии и распада твердого вещества, находящегося в подвижной вязкой и одновременно тяжелой жидкой среде.
Для проведения работ по сопоставлению имеющихся в наличии данных натурных измерений и данных лабораторных опытов достаточно этих пяти критериев подобия. Для обеспечения полного подобия соответствующие комплексы должны быть примерно одинаковыми по величине.
В отсутствии данных лабораторного опыта необходимо провести следующие исследования:
– провести анализ приведенных критериев подобия;
– получить соотношения по выбору параметров в лабораторном опыте, включая выбор
временного масштаба измерений.
Выполним вначале намеченные пункты исследования для пяти приведенных выше критериев.
Согласно теории подобия изложенной в [4] введем коэффициент геометрического подобия ![]() в виде отношения линейного размера оригинала
в виде отношения линейного размера оригинала ![]() к линейному размеру модели
к линейному размеру модели ![]() , т.е.
, т.е.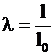 . (7)
. (7)
Величина ![]() указывает во сколько раз характерный линейный размер оригинала больше характерного линейного размера модели.
указывает во сколько раз характерный линейный размер оригинала больше характерного линейного размера модели.
Выделим в критерии подобия Фруда ![]() величину коэффициента геометрического подобия
величину коэффициента геометрического подобия ![]() согласно (7), учтем, что все испытания проходят только в земном поле силы тяжести и величина
согласно (7), учтем, что все испытания проходят только в земном поле силы тяжести и величина ![]() .
.
Из критерия подобия Фруда, приведенного в формулах (5), следует соотношение для величины отношения скоростей движения в жидкой среде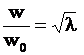 . (8)
. (8)
Видно, что скорость движения для модельного объекта ![]() должна быть в
должна быть в ![]() раз меньше скорости движения натурного объекта
раз меньше скорости движения натурного объекта![]() в (8).
в (8).
Подставим отношение скоростей (8) в критерий подобия Рейнольдса ![]() , приведенный в формулах (5), получим соотношение для отношения коэффициентов кинематической вязкости используемых жидких растворителей
, приведенный в формулах (5), получим соотношение для отношения коэффициентов кинематической вязкости используемых жидких растворителей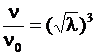 . (9)
. (9)
Видно, что коэффициент кинематической вязкости растворителя для модельного объекта ![]() должен быть в
должен быть в ![]() раз меньше коэффициента кинематической вязкости растворителя для натурного объекта
раз меньше коэффициента кинематической вязкости растворителя для натурного объекта![]() .
.
Подставим отношение скоростей (9) в критерий подобия диффузионных процессов в подвижной среде ![]() , приведенный в формуле (6), получим соотношение для отношения коэффициентов диффузии используемых жидких растворителей
, приведенный в формуле (6), получим соотношение для отношения коэффициентов диффузии используемых жидких растворителей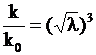 . (10)
. (10)
Видно, что коэффициент диффузии растворителя для модельного объекта ![]() должен быть в
должен быть в ![]() раз меньше коэффициента диффузии растворителя для натурного объекта
раз меньше коэффициента диффузии растворителя для натурного объекта![]() в (10).
в (10).
Подставим отношение скоростей в критерий подобия Эйлера ![]() , приведенный в формулах (5), получим формулу для отношения плотностей применяемых растворителей
, приведенный в формулах (5), получим формулу для отношения плотностей применяемых растворителей 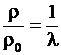 . (11)
. (11)
Видно, что плотность жидкости растворителя для модельного объекта ![]() должен быть в
должен быть в ![]() раз больше плотности жидкости растворителя для натурного объекта
раз больше плотности жидкости растворителя для натурного объекта ![]() в (11).
в (11).
Подставим отношение скоростей в критерий химического подобия Дамкеллера-![]() , приведенный в формулах (5), получим формулу для отношения коэффициентов распада применяемых твердых примесей
, приведенный в формулах (5), получим формулу для отношения коэффициентов распада применяемых твердых примесей
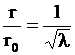 . (12)
. (12)
Видно, что коэффициент распада твердой примеси для модельного объекта ![]() должен быть в
должен быть в ![]() раз больше коэффициент распада твердой примеси для натурного объекта
раз больше коэффициент распада твердой примеси для натурного объекта ![]() .Полученные соотношения между параметрами модельного и натурного объекта (7)–(12) являются нелинейными относительно значения коэффициента геометрического подобия
.Полученные соотношения между параметрами модельного и натурного объекта (7)–(12) являются нелинейными относительно значения коэффициента геометрического подобия![]() . Скорость потока, кинематическая вязкость и коэффициент диффузии в жидкости модели уменьшаются по сравнению со значениями оригинала. Плотность жидкости и величина коэффициента распада вещества в жидкости модели возрастают по сравнению со значениями параметров оригинала.
. Скорость потока, кинематическая вязкость и коэффициент диффузии в жидкости модели уменьшаются по сравнению со значениями оригинала. Плотность жидкости и величина коэффициента распада вещества в жидкости модели возрастают по сравнению со значениями параметров оригинала.
Процесс измерений в натурном эксперименте и модельном опыте разворачивается во времени.
Чтобы завершить проведенное исследование необходимо провести выбор масштаба временного масштаба измерений, точно согласовав его с остальными безразмерными критериями подобия.
Наиболее удобный путь согласования масштабов измерения состоит во введении критериев подобия непосредственно в решаемом уравнении. Рассмотрим уравнение диффузии изотопа![]() .
.
Введем новые безразмерные комплексы непосредственно в уравнении с помощью безразмерных переменных следующего вида![]()
![]() .
.
Величина ![]() равна выбранному характерному значению концентрации переносимой потоком и подверженной распаду твердой примеси. Функция
равна выбранному характерному значению концентрации переносимой потоком и подверженной распаду твердой примеси. Функция ![]() описывает концентрацию этой примеси в безразмерной форме. Величина
описывает концентрацию этой примеси в безразмерной форме. Величина ![]() равна некоторому характерному значению для времени измерений в натурном измерении. Значение величины
равна некоторому характерному значению для времени измерений в натурном измерении. Значение величины ![]() предстоит выбрать. Переменная
предстоит выбрать. Переменная ![]()
равна безразмерному времени. Величина ![]() характеризует линейный натурный размер, поэтому
характеризует линейный натурный размер, поэтому![]() безразмерная пространственная координата.
безразмерная пространственная координата.
Введем безразмерные переменные ![]() в нашем дифференциальном уравнении
в нашем дифференциальном уравнении
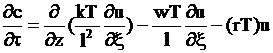 .
.
Два множителя в виде дробей перед частной производной по переменной![]() не имеют размерности. Множитель в круглой скобке последнего слагаемого данного дифференциального
не имеют размерности. Множитель в круглой скобке последнего слагаемого данного дифференциального
уравнения также не имеет размерности. При произвольном характерном значении времени ![]() имеется три безразмерных комплекса. Выгодно сократить число безразмерных комплексов до двух, что упрощает задачу управления не только процессом вычислений, но процессом управления экспериментом.
имеется три безразмерных комплекса. Выгодно сократить число безразмерных комплексов до двух, что упрощает задачу управления не только процессом вычислений, но процессом управления экспериментом.
Положим, что характерное время измерений ![]() равно отношению характерного линейного размера оригинала к скорости потока жидкости в натурном эксперименте
равно отношению характерного линейного размера оригинала к скорости потока жидкости в натурном эксперименте ![]() .
.
Второй безразмерный комплекс в точности равен единице при таком выборе ![]() . В остальных случаях выводим два безразмерных комплекса, которые использовались нами ранее
. В остальных случаях выводим два безразмерных комплекса, которые использовались нами ранее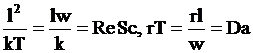 .
.
Согласование выбора неизвестной временной постоянной ![]() завершено оптимальным образом.
завершено оптимальным образом.
Изучим теперь безразмерный комплекс, равный по величине безразмерному времени ![]()
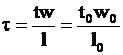 .
.
Найдем отношение времени реального процесса![]() к времени в модельном процессе
к времени в модельном процессе ![]()
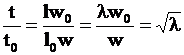 . (13)
. (13)
Видно, что при проведении лабораторного эксперимента время наступления некоторого события ![]() сокращается в
сокращается в![]()
![]() раз по сравнению со временем наступления этого же события
раз по сравнению со временем наступления этого же события ![]() в натурном эксперименте.
в натурном эксперименте.
Согласно (13) ожидаемая частота процесса возрастает в![]() раз при уменьшении размеров модели, что качественно соответствует наблюдениям в различных приложениях механики сплошной среды и динамики машин, а также в ряде новых технологий производства, охраны труда и безопасности жизнедеятельности.
раз при уменьшении размеров модели, что качественно соответствует наблюдениям в различных приложениях механики сплошной среды и динамики машин, а также в ряде новых технологий производства, охраны труда и безопасности жизнедеятельности.
На рисунке 1. изображены критерии подобия в виде степенных функций одного параметра ![]() ,
,
который имеет смысл параметра геометрического подобия, определенного в формуле (7). В формулах (7)-(13) приведено всего шесть критериев подобия. На рисунке 1 приведено всего
пять степенных зависимостей, что обусловлено совпадением вида степенной зависимости в критериях подобия (9) и (10). Критерий подобия (9) определен для коэффициента кинематической
вязкости. Критерий подобия (10) определен для коэффициента диффузии. Оба коэффициента обладают одинаковой размерностью. Совпадение размерности коэффициентов и одновременно выбор временного масштаба позволил минимизировать число разных рассматриваемых здесь степенных безразмерных зависимостей. Показатели степени указаны в виде цифры, расположенной над соответствующим безразмерным критерием на рисунке 1. При значениях
параметра ![]() три зависимости из всех пяти зависимостей расположены ниже закона геометрического подобия.
три зависимости из всех пяти зависимостей расположены ниже закона геометрического подобия.
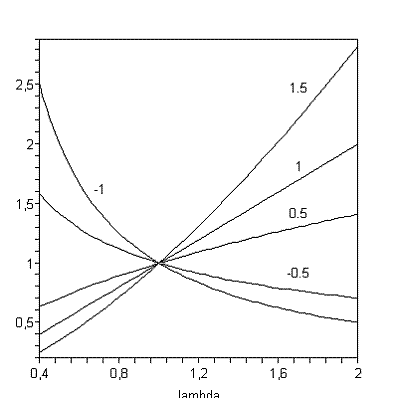
Рисунок 1. Критерии подобия в виде степенных функций параметра ![]()
Одновременное совмещение всех критериев и зависимостей, определенных в формулах (7)–(13), в лабораторном эксперименте на копии и модели затруднительно в силу их нелинейности, однако это не является кардинальным препятствием для проведения пересчета и проецирования результатов лабораторного опыта на натурный эксперимент в подвижной жидкости при соблюдении определенных мер[5]. Минимизация числа разных нелинейных зависимостей,рассмотренных здесь, способствует снижению этих трудностей. Результаты работы применимы в проблеме повышения уровня достоверности для метода акустической эмиссии при оценке кинетики сольватизации [6] c учетом дополнительных факторов: подвижность вязкой среды, давление в потоке текущей жидкости. В целом результаты исследования могут быть использованы при сопоставлении, анализе данных натурного и лабораторного эксперимента для решения ряда задач охраны труда и безопасности в чрезвычайных ситуациях.
Литература
1. Айзатуллин Т.А., Лебедев В.Л., Хайлов К.М. Океан. Активные поверхности и жизнь. Л.
Гидрометеоиздат.1979, 192 с.
2.Поль Р.В. Механика, акустика и учение о теплоте. М. Наука, 1971, - 480 с.
3. Шаповалов Л.А. Моделирование в задачах механики элементов конструкций. - М.: Машиностроение, 1990-288с.
4. Бухгольц Н.Н. Основной курс теоретической механики. Изд.7, Ч. 2. Изд-во Лань, 2009, 336 с.
5. Клейтон Б., Бишоп Р. Механика морских судов- Л.: Судостроение, 1986.- 436 с.
6. Гапонов В.Л. , Буйло С. И. .Кузнецов Д.М., Трепачев В.В.. Азимова Н.Н. О достоверности
метода акустической эмиссии для оценки кинетики сольватизации //Вестник развития науки и образования. 2010. №5 С.42-51.