Алгоритм и программная реализация адаптивного метода обучения искусственных нейронных сетей
Аннотация
В статье предлагается общий для всех градиентных методов– адаптивный метод. С помощью разработанной экспериментальной среды был проведен сравнительный анализ градиентных методов поиска минимума. В результате экспериментов было выявлено, что адаптивный метод приближается к минимуму за меньшее число итераций. Таким образом предлагается использовать данный метод при оптимизации функции ошибки обучения искусственной нейронной сети.
Ключевые слова: нейронные сети, градиентные методы, методы обучения, анализ методов оптимизации.Ключевые слова:
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Задача обучения искусственной нейронной сети (ИНС) может рассматриваться как задача оптимизации, при этом основная проблема заключается в выборе среди разнообразных оптимизационных методов наиболее подходящего[1,2,3,4,5].
В основном все оптимизационные алгоритмы можно разбить на три категории:
- методы случайного поиска;
- методы стохастического градиентного спуска;
- градиентные методы.
К группе градиентных методов относятся следующие методы:
- метод градиентного спуска;
- метод тяжелого шарика;
- методы сопряженных градиентов.
Выбор в пользу градиентных методов обоснован тем, что, как правило, в задачах обучения критерий обучения можно выразить в виде дифференцируемой функции от весов нейронной сети. Тем не менее, неопределенность выбора метода обучения сохраняется. В автоматизированных системах нейро-сетевого программирования следует стремиться к сокращению неопределенности, которая присуща этим технологиям. Неопределенность в выборе алгоритма обучения в некоторой степени устраняется в предлагаемом ниже адаптивном методе обучения.
Общий анализ градиентных методов обучения нейронных сетей позволяет утверждать, что любой из этих методов можно представить как частный случай предлагаемого алгоритма.
Общую формулу для изменения весов выразим формулой (1):
![]() , (1)
, (1)
где вектор![]() задает направление движения, а
задает направление движения, а ![]() - размер шага на k-ой итерации.
- размер шага на k-ой итерации.
Формулу расчета вектора![]() выразим следующим образом:
выразим следующим образом:
![]() ,(2)
,(2)
где вектор ![]() задает направление движения;
задает направление движения;![]() - направление антиградиента на j-ой итерации;
- направление антиградиента на j-ой итерации; ![]() - коэффициент, определяющий вес i-го градиента; m определяет кол-во запоминаемых градиентов; k – порядковый номер текущей итерации.
- коэффициент, определяющий вес i-го градиента; m определяет кол-во запоминаемых градиентов; k – порядковый номер текущей итерации.
Градиентный метод обучения из формулы 2 получается при ![]() . А методы сопряженных градиентов[1], которые наиболее часто употребляются при обучении нейронных сетей, получаются путем суммирования всех предыдущих направлений (при
. А методы сопряженных градиентов[1], которые наиболее часто употребляются при обучении нейронных сетей, получаются путем суммирования всех предыдущих направлений (при![]() ).
).
Таким образом, предлагаемый адаптивный алгоритм является более гибким решением при обучении нейронных сетей.
Общий алгоритм адаптивного метода:
- Начало
- Выбираем стартовую точку с некоторыми координатами (x0;y0;...).
- Проверяем критерий остановки (число итераций, средняя квадратическая ошибка и др)
- Вычисляем антиградиент в текущей точке (на первой итерации стартовая точка).
- Заносим текущее направление в стек направлений.
- Считаем вектор направления по формуле 2.
- Перемещаемся по вычисленному вектору в новую точку.
- Возвращаемся в шаг 2. Если критерий остановки положителен, то заканчиваем алгоритм, если нет – переходим к шагу 3.
- Конец алгоритма. Имеем точку, близкую к минимуму функции.
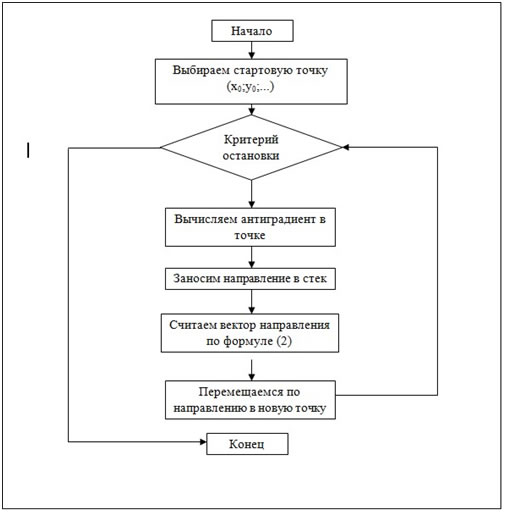
Рис. 1. Общий алгоритм адаптивного метода
Рассмотрим пример использования такого подхода при оптимизации функции Розенброка [2]: ![]() (3)
(3)
Вычисление минимума функции Розенброка считается трудной проблемой для итерационных методов поиска минимума.
Для проведения экспериментов было разработано программное обеспечение на платформе Microsoft .NET на языке C#.
Проведены эксперименты, из одной стартовой точки с координатами (-1.5; 3.5), с изменением параметров: η, m, β.
Для градиентного спуска (m=0), при оптимальном η=0.005 значение целевой функции - 0.30103179 достигается на 121-ой итерации. Движение и изменение значений функции изображено на рис. 2.
Для метода тяжелого шарика[1] , который также является частным случаем адаптивного метода, при m = 1, β=0.9 и η=0.005, значение целевой функции 0.12836612 достигается на 52-ой итерации. Результаты вычислений представлены на рис. 3.
Для адаптивного алгоритма с параметрами η=0.0004, m = 2, β = (0.9,0.081) значение целевой функции - 0.04807101 получено на 35-ой итерации. Результаты расчетов представлены на рис. 4.
Таким образом, для сложной функции Розенброка (3) адаптивный алгоритм оказался лучшим, по сравнению с классическими методами: градиентного спуска и тяжелого шарика.
Применение адаптивного алгоритма для обучения нейронных сетей требует настройки параметров: m, β и h . В связи с этим предлагается следующий адаптивный метод обучения ИНС, на основе адаптивного алгоритма.
Обозначим через ИНС 1 – основную нейронную сеть, которая будет обучаться на реальных данных - обучающей выборке 1 с помощью настроенного адаптивного алгоритма. Для настройки параметров алгоритма обучения используется ИНС 2, топологически вложенная в ИНС 1 и обучающая выборка 2, полученная путем случайного отбора некоторых примеров обучающей выборки 1. Для сокращения числа настраиваемых параметров воспользуемся представлением![]() , где
, где![]() .
.
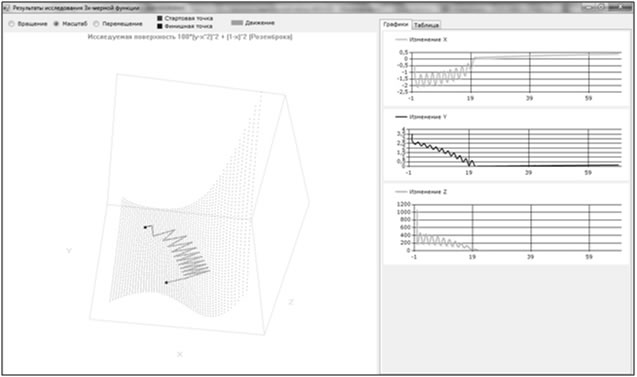
Рис. 2. Метод градиентного спуска, с шагом 0.005
Контроллер, обучающий ИНС 2 в автоматическом режиме на примере обучающей выборки 2, подбирает оптимальные параметры для адаптивного алгоритма. Критерием при этом является минимум числа итераций необходимых для достижения минимума.
После чего оптимальные параметры обучения передаются в ИНС 1 для обучения на реальных данных.
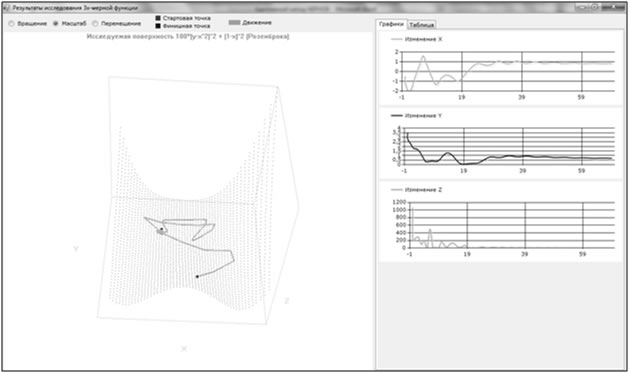
Рис. 3. Метод тяжелого шарика с m =1, β = 0.9 и шагом 0.001

Рис. 4. Адаптивный алгоритм, шаг 0.0004, m=2 и β = (0.9,0.081).
Предложенный метод обучения сводит к минимуму вмешательство человека в обучение ИНС, что делает его привлекательным. Поскольку не каждый пользователь ИНС-технологий владеет знаниями в области методов оптимизации. Кроме этого метод является гибким и настраиваемым на обучающую выборку методом обучения.
Список использованной литературы
1.Тархов Д.А. Нейронные сети. Модели и алгоритмы. Кн.18. Справочное издание. (Серия 'Нейрокомпьютеры и их применение'): – М.: Радиотехника, 2005. – 256с.
2.Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. – М.: Горячая линия – Телеком, 2002. – 382с.: ил.
3.Пучков Е.В., Лила В.Б. Применение градиентных методов оптимизации для обучения искусственных нейронных сетей на примере задачи прогнозирования временного ряда. – Нечеткие системы и мягкие вычисления: сб. ст. Третьей Всероссийской научной конференции: В 2.т. Т. I / Волгоград. гос. техн. ун-т; редкол.: А.В. Заболеева-Зотова (отв. ред.) [и др.]. – Волгоград, 2009. – 214с. с.109-116.
4.Хайкин С. Нейронные сети: полный курс, 2-е издание. : Пер. с англ. – М.: Издательский дом «Вильямс», 2006. – 1104 с.: ил. – Парал. тит. англ.
5.Бэстен Д.-Э., ванн ден Берг В.-М., Вуд Д. Нейронные сети и финансовые рынки: принятие решений в торговых операциях. – Москва: ТВП, 1997.-236с.