Сравнение параметра сдвига распределения совокупностей исходной и полученной вычислительным экспериментом для показателей надежности деталей
Аннотация
В данной работе выполнен сравнительный анализ параметра сдвига распределения исходной совокупности, вычисленной аналитическим методом, и моделированной, полученной с помощью компьютерного эксперимента с использованием выборочных данных. Погрешности δi между параметрами сдвигов занесены в таблицы и построены графики зависимостей погрешностей от размаха и объёма совокупности.
Таким образом, с увеличением объема совокупности погрешность уменьшается с 30% до 1% при постоянном объеме выборки m=50.
Ключевые слова: выборка, совокупность, объем, размах, погрешность, распределение, анализ параметров, машиностроение, надёжность.Ключевые слова:
05.05.04 - Дорожные, строительные и подъемно-транспортные машины
Повышение надежности строительных машин, является одним из основных направлений машиностроительной отрасли, разработка которого влечет за собой решение не только технических, но и экономических задач. Очень важно на стадии проектирования обеспечить почти безотказную работу машины в течение заданного ресурса. Для определения точности перехода от выборочных данных показателей надежности к данным совокупности найдены погрешности δi параметров сдвига исходной совокупности и совокупности конечного объема (далее совокупности),полученной в результате эксперимента.
Проведен вычислительный эксперимент по алгоритму аналитического метода (рис. 1)[1].
С помощью моделирования найдены параметры (Ас,Вс,Сс). Для выборок (прочности, ресурса) с различными размахами и объемами найдены параметры (a,b,c), затем с помощью аналитического метода по алгоритму (рис.1) определены параметры Ас, Вс, Сс исходной совокупности.
Выполнен вычислительный эксперимент, по которому из исходной совокупности объемом Nc=103,104,105,106 с помощью моделирования получены выборки, объемом n=50 в количестве m=50 шт. с различными размахами:R=1,1;50;100. Далее для каждой выборки найдены параметры Aci, Bci, Cci.
Впоследствии определены погрешности δi между параметрами сдвигов распределения исходной совокупности и полученными в результате вычислительного эксперимента
![]() .
.
Значение погрешностей занесены в таблицы (1-4), на основании которых построены графики (рис.2 - 5) зависимости, ошибки от размаха для каждого из объёмов совокупности.

Рис.1. Блок-схема алгоритма расчета параметров распределения Вейбулла для совокупности по выборке
Таблица 1
Значение ошибок в зависимости от размаха при объеме совокупности 103.
|
R |
δмин |
δср |
δмакс |
|
1,1 |
0,26 |
31,88 |
65,41 |
|
50 |
0,06 |
11,40 |
41,22 |
|
100 |
0,32 |
7,18 |
29,53 |
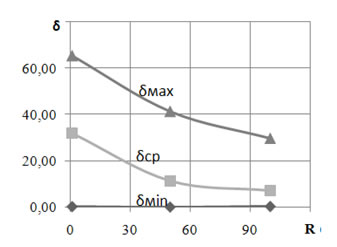
Рис.2. Зависимость ошибки δ от размаха R при объеме совокупности 103.
Таблица 2
Значение ошибок в зависимости от размаха при объеме совокупности 104.
|
R |
δмин |
δср |
δмакс |
|
1,1 |
0,24 |
17,65 |
43,95 |
|
50 |
0 |
2,658005 |
14,7016 |
|
100 |
0,063633 |
5,701423 |
27,37572 |
Рис.3. Зависимость ошибки δ от размаха R при объеме совокупности 104.
Таблица 3
Значение ошибок в зависимости от размаха при объеме совокупности 105.
|
R |
δмин |
δср |
δмакс |
|
1,1 |
0,13 |
9,41 |
19,03 |
|
50 |
0,00 |
1,90 |
12,49 |
|
100 |
0,00 |
4,64 |
20,44 |
Рис.4. Зависимость ошибки δ от размаха R при объеме совокупности 105.
Таблица 4
Значение ошибок в зависимости от размаха при объеме совокупности 106.
|
R |
δмин |
δср |
δмакс |
|
1,1 |
0,20 |
8,09 |
18,49 |
|
50 |
0,00 |
1,75 |
11,06 |
|
100 |
0,00 |
4,81 |
23,71 |
Рис.5. Зависимость ошибки δ от размаха R при объеме совокупности 106.
Занесли средние значения погрешностей в таблицу, и на основании вычисленных значений построили график зависимости средних значений погрешностей относительно объёма выборок для каждого из размахов.
Таблица 5
Зависимость ошибки от размахов и объемов совокупностей.
|
RNc |
103 |
104 |
105 |
106 |
|
1,1 |
31,88 |
17,65 |
9,41 |
8,09 |
|
50 |
11,40 |
2,66 |
1,90 |
1,75 |
|
100 |
7,18 |
5,70 |
4,64 |
4,81 |
Рис.6. Зависимость ошибки от объемов совокупностей.
Из графиков видно, что при размахе R=50 погрешность принимает наименьшее значение.
Для определения зависимости относительной погрешности δ при сравнении компьютерного эксперимента и аналитического метода при определении сдвигов для различных размахов и объемов совокупностей построили 3-х мерную поверхность.
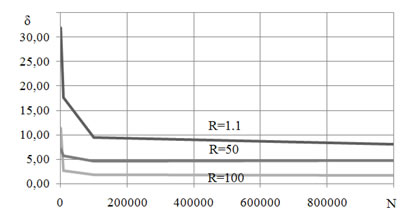
Рис.5. Зависимость ошибки от размаха и объема совокупности.
Из графика видно, что с увеличением объема совокупности погрешность уменьшается с 30% до 1% при постоянном объеме выборки m=50.
Вместе с этим следует отметить, что с увеличением объема выборки до объема совокупности ошибка стремится к нулю, т.е. имеет место обратная зависимость. Поэтому требуется дополнительно исследовать эту зависимость.
Список литературы:
1. Касьянов В.Е., Зайцева М.М., Котесова А.А., Котесов А.А. Оценка параметров распределения Вейбулла для совокупности конечного объема. Деп. ВИНИТИ № 21-В2012 от 24.01.12