Технологии топологической оптимизации трафика информационных потоков в телекоммуникационных сетях

Аннотация

Д.Е. Рудь

В статье проводится сравнительный анализ алгоритмов маршрутизации, позволяющих оптимизировать сеть по интегральному критерию качества обслуживания. Особое внимание уделяется многопутевым методам передачи данных, а также количеству операций, необходимому для их выполнения (сложность алгоритма). Кроме традиционных алгоритмов, в статье делается попытка оценки использования методов линейного программирования с целью решения вышеупомянутой задачи.
Ключевые слова: телекоммуникационная сеть, адаптивная маршрутизация, теория графов, динамическое программирование, линейное программирование.
Стр. 95-107
№ гос. регистрации 0421000096\0018

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Быстрый рост числа компьютерных сетей, успехи в развитии проводных и беспроводных средств связи сопровождается непрерывной сменой сетевых технологий, направленной на повышение быстродействия и надежности сетей. Для стран, в которых большая территория сочетается с невысокой плотностью населения, телекоммуникационные сети имеют особое значение, так как позволяют экономично и оперативно создавать промышленную инфраструктуру на обширных территориях [1]. Особенно это важно для информатизации удаленных и сельских регионов Российской Федерации и решения одной из важнейших проблем информационной безопасности России – проблемы «информационного неравенства» российских регионов. В ситуации, когда кабельная сеть недостаточно развита (что характерно для России и многих других стран) и постоянно возрастает спрос на информационные услуги, применение эффективной системы управления потоками информации  позволило бы учесть возникающие изменения в ситуации на сети и обеспечить в изменяющихся условиях сохранение заданного значения обобщенного критерия качества обслуживания. В связи с этим весьма актуальной является разработка новых принципов топологической оптимизации трафика с последующим внедрением их в существующих сетях через протоколы маршрутизации.

Общие принципы топологической оптимизации сетей
При организации сетей одной из основных задач является распределение потоков информации по кратчайшим путям. Под такими путями понимают пути передачи информации, кратчайшие по времени передачи или протяженности, или пути с минимальными помехами, числом задействованных узлов, стоимостью и т.п. Таким образом, оптимизация путей может проводиться по различным технико-экономическим критериям и выбранные пути должны обеспечивать при заданных требованиях наиболее эффективное использование линий и узлов связи. В связи с этим имеет смысл проведение сравнительного анализа существующих на сегодняшний день алгоритмов маршрутизации с целью выработки закономерностей эволюции развития топологии и методики управления информационными потоками.
Было выявлено, что использование адаптивной маршрутизации может уменьшить среднее время нахождения пакета в сети, позволяет минимизировать затраты на его доставку получателю в сетях с разнородным трафиком, увеличить общую надежность сети за счет возможности автоматического выбора альтернативного маршрута на основании данных о топологии сети. Однако, данные преимущества достигаются увеличением нагрузки на вычислительные центры узлов коммутации, поэтому использование адаптивной маршрутизации ограничено размерами автономной системы (домена). Очевидно, что при этом возникает проблема разработки математического обеспечения оптимизации процедур выбора маршрута с целью снижения нагрузки на вычислительные центры, а также получения возможности использования многопутевой маршрутизации.
На этапе выбора оптимального маршрута для отправки пакетов следующему узлу сеть будем рассматривать как взвешенный ориентированный граф. Вершины графа представ­ляют маршрутизаторы, а дуги, соединяющие эти вершины, - физические линии между вершинами. Каждой линии связи соответствует некоторое интегральное значение, представ­ленное посредством «стоимости» пересылки пакета по ней, которое может зависеть как от физической длины линии, временных затрат при передаче данных, так и от финансовых издержек транспортировки пакета. В настоящее время известен ряд алгебраических методов [2,3,4], позволяющих в определенной степени  описать этот процесс с тем, чтобы получать результаты в форме, удобной для последую­щих исследований. А для этого необходимо сделать усилия по классификационному мониторингу известных методов с целью оценки их прикладной значимости и ограничений их использования.

Методы динамического программирования.
Задачам отыскания кратчайших путей передачи информации присущи три основных свойства динамического программирования: многоходовой выбор, аддитивность и независимость оптимального пути от предыстории. В самом деле, исследование процесса передачи сообщений от узла к узлу в сети распадается на отдельные этапы (многоходовой выбор); длина пути, состоящего из нескольких ветвей, равна сумме длин этих ветвей (свойство аддитивности), и, наконец, кратчайший путь передачи сообщений из какого-либо узла не зависит от того, как сообщение попало в этот узел, а только от расположения этого узла в сети (свойство независимости от предыстории) [2]. На практике нашли применение: метод Флойда-Уоршелла, метод Беллмана-Форда, а также менее известный матричный метод.
Метод Флойда-Уоршелла [3], основанный на понятиях о базисной линии связи и тернарной операции, применяется для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного графа.  Достоинства данного метода – простота реализующего алгоритма и возможность получения маршрутной информации сразу для всех узлов сети, что делает его применение целесообразным при централизованных структурах управления информационными потоками. Говоря о сложности данного метода при программной реализации, стоит отметить, что три вложенных цикла содержат операцию, исполняемую за константное время, то есть алгоритм имеет кубическую сложность [4]. В настоящее время существуют способы ускорения систем, использующих данный метод, позволяющих снизить сложность с  до , где n– количество узлов сети. Речь идет об использовании битовых масок (в модели с промежуточным хранением результатов вычислений в RAM) и специализированных наборах микропроцессорных команд, как SSE (Streaming SIMD Extensions), в которых преимущество в производительности достигается в случае проведения одной и той же последовательности операций над разными данными.
Метод Беллмана-Форда [5] применяется для поиска кратчайшего пути во взвешенном графе. Основным достоинством является возможность расчета пути в графе, в котором есть ребра с отрицательным весом. Для подсчета кратчайшего пути этим методом требуется провести всего  циклов, но на практике этот алгоритм можно использовать и для отслеживания отрицательных циклов, проведя ровно n циклов. Если при исполнении последней итерации длина кратчайшего пути до какой-либо вершины строго уменьшилась, то в графе есть отрицательный цикл. Можно отслеживать изменения в графе и, как только они закончатся, дальнейшие итерации будут бессмысленны. Данный метод используется в протоколе маршрутизации RIP (Routing Information Protocol) и его модификациях, причем некоторые его модифицированные версии задействованы в небольших сетях (не более 15 рабочих станций), в которых не требуется больших вычислительных мощностей для расчета путей, а также - для сетей с почти неизменной структурой.
Матричный метод определения кратчайших путей между всеми узлами сети был предложен Шимбелом [6] и усовершенствован Оттерманом [7]. Возможность полного топологического анализа сети обеспечила широкое практическое применение этого метода при организации трафика передачи данных в сетях.
При определении кратчайших путей матричным методом выполняются следующие операции:

1. По графу телекоммуникационной сети (Т-сеть) составляется матрица весов ветвей .
2. Матрица весов  преобразуется по правилам умножения матриц, но с использованием специальных операций Шимбела [6], в дисперсионную матрицу кратчайших путей между узлами сети, т.е.

.

Однако, матричный метод позволяет не только определить величины кратчайших путей между всеми узлами сети, но также одновременно получить длины всех возможных путей между каждой парой узлов сети. Это дает возможность использовать матричный метод для отыскания в сети обходных путей. Объем вычислений при использовании матричного метода незначительно зависит от структуры сети. Метод удобен для программной реализации.

Графовые алгоритмы в топологии сети
Особое место в математическом обеспечении детерминированных процедур выбора трафика передачи информационных потоков занимают методы Флойда и Дейкстры, базирующиеся на принципе оптимальности.
Метод Дейкстры [4] позволяет находить кратчайшие пути от одной из вершин графа до всех остальных. Метод работает только для графов без ребер отрицательного веса, хотя в настоящее время существуют обобщенные методы для устранения данного недостатка (метод Дейкстры с потенциалами). Суть метода Дейкстры состоит в поэтапном наращивании дерева кратчайших маршрутов от исходного узла. При этом необходимо, чтобы после добавления на каждом этапе линии связи и узла вновь образуемый кратчайший маршрут был минимально возможным по всем оконечным узлам, еще не вошедшим в дерево. В процессе построения дерева кратчайших маршрутов вычисляются векторы весов маршрутов и корректируются векторы начальных компонент кратчайших маршрутов. Сложность метода Дейкстры зависит от способа нахождения вершины v, а также от способа хранения множества непосещенных вершин и способа обновления меток. В графе G, nи m соответственно количество вершин и ребер для поиска вершины с минимальной длиной пути до вершины v, просматривается все множество n. Время работы алгоритма минимизации есть . Для разряженных графов (для таких, для которых ) при использовании специальных алгоритмов оптимизации [8] скорость работы может составить  или даже . Метод Дейкстры широко применяется в сетевом программировании и технологиях, например, его используют в протоколе OSPF (Open Shortest Path First) для устранения кольцевых маршрутов. Использование модифицированного алгоритма Дейкстры, как эффективного инструмента для распределения входных информационных потоков в магистральных IP-сетях с протоколом OSFP, позволяет улучшить робастность сети к информационным перегрузкам [9]. При этом возможно в качестве критерия распределения информационных потоков использовать остаточную пропускную способность канала. Необходимо отнести к положительным качествам протокола относительную простоту практической реализации метода.
Метод Джонсона [4] позволяет найти кратчайшие пути между всеми парами вершин взвешенного ориентированного графа. Данный метод работает, если в графе содержатся ребра с положительным или отрицательным весом, но отсутствуют циклы с отрицательным весом. В методе Джонсона используется метод Беллмана-Форда и метод Дейкстры, реализованные в виде подпрограмм. Ребра хранятся в виде списков смежных вершин. Если в методе Дейкстры неубывающая очередь с приоритетами реализована в виде фибоначчиевого множества, то время работы метода Джонсона равно . При более простой реализации неубывающей очереди с приоритетами время работы становится равным , но для разреженных графов эта величина в асимптотическом пределе ведет себя с точки зрения нечеткого критерия логики лучше, чем время работы алгоритма Флойда-Уоршелла.

Метод линейного программирования.
Определение кратчайшего пути методом линейного программирования – задача отыскания экстремума некоторой аддитивной функции, значения которой ограничены пространством, описываемым системой уравнений и неравенств. Этот метод позволяет оптимизировать пути по какому-либо неизвестному параметру ветвей. В других методах оптимизации параметры ветвей Т-сети задаются [2].
Процесс передачи информации в сети будет оптимальным, если распределить допустимые времена передачи информации по отдельным ветвям Т-сети так, чтобы среднее время передачи информации по пути было минимальным. Для этого в качестве исходного условия положим общее время, затрачиваемое на передачу информационных потоков по каждому пути, не превысит установленного для данного пути допустимого времени . Процесс следования информационного потока  по i-му пути сети при условии, что трафики отдельных ветвей независимы, может быть описан следующим линейным алгебраическим неравенством:
,
где  - число  пакетов, передаваемых по i-му пути в j-й ветви; ; ; n – максимальное число ветвей в сети;  - число возможных путей в сети;  - время передачи одного пакета по j-й ветви;  - допустимое время следования информационного потока по i-му пути.
Если в сети возможны  путей, то, следовательно, может быть получена система  линейных алгебраических неравенств: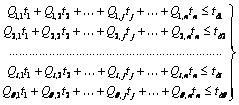

Для решения системы линейных неравенств составляется линейная форма (целевая функция):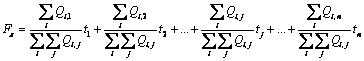
 неизвестных  .
Среди всевозможных неотрицательных решений  системы линейных неравенств определяется такое решение , при котором линейная функция  принимает наименьшее возможное значение. Очевидно,  линейная функция  описывает время следовании информационного потока по выбранному пути сети. Решение рассмотренной задачи линейного программирования позволяет оптимальным образом оценить временной ресурс трафика передачи пакетов по ветвям топологии сети при минимизации среднего времени передачи пакета по пути.

Выводы

Список источников:

1. Вишневский В. М. Теоретические основы проектирования компьютерных сетей. – М.: Техносфера, 2003. – 512 с.: ил;
2. Овчинников В.Н. Организация передачи информации в автоматизированных системах управления. – М.: Энергия, 1974. - 128 с.: ил;
3. Левитин А. В. Алгоритмы: введение в разработку и анализ. — М.: «Вильямс», 2006. — с. 349 — 353;
4. Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: Вильямс, 2006. — с. 1296;
5. Bellman R. On a Routing Problem // Quarterly of Applied Mathematics. 1958. Vol 16, No. 1. C. 87-90, 1958;
6. Shimbel A. Structural Parameters of Communication networks, 1953, v.15, № 4;
7. Otterman J. Matrix Multiplication in Search for Alternate Routes, 1963, v.38, № 2;
8. http://www.intuit.ru/department/algorithms/dscm/7/2.html
9. Кузнецов Н. А., Фетисов В. Н. «Алгоритм Дейкстры с улучшенной робастностью для управления маршрутизацией в IP-сетях», Автоматика и телемеханика, № 2, 2008;
10. Дэвис Д., Барбер Д. Сети связи для вычислительных машин. – М.: Мир, 1976. – 680 с.
11. Нечипоренко В. И. Структурный анализ систем. – М.: Сов. радио, 1977. – 21