Расчёт цилиндрических тел при воздействии теплового и радиационного нагружений

Аннотация

С.В. Литвинов, Ю.Ф. Козельский, Б.М. Языев

  Приводится задача расчёта напряжений в радиационно-тепловом экране АЭС. Данная конструкция, называемая также «сухой защитой» предназначена для снижения радиационных и тепловых воздействий, генерирующихся при работе реактора. Показано значительное перераспределение напряжений в результате изменения модуля упругости за счёт вышеуказанных воздействий.

Ключевые слова: тепловое нагружение, радиационное нагружение, расчёт защиты при аварийном режиме

05.23.17 - Строительная механика

При воздействии на бетон высоких температур, радиационного воздействия и т.д., его физико-механические свойства могут изменяться, что сказывается на напряжённо-деформированном состоянии.
В статье проводится расчёт бетонного цилиндрического тела в плоской постановке (плоское деформированное состояние). Внутренний и внешний радиусы цилиндра соответственно r_a и r_b.
Дифференциальное уравнение, описывающее распределение радиальных напряжений вдоль радиуса цилиндра, хорошо известно [1]:
,                                                   
где: , , .
Как было сказано выше, модуль Юнга зависит от температурной и радиационной нагрузок, т.е.:
.
Коэффициент Пуассона принят постоянной величиной, что объясняется ограниченностью экспериментальных данных о его изменении под действием вышеуказанных факторов.
.
Здесь:  – вынужденная деформация;  – температурная деформация;  – деформация в результате радиационного воздействия;  – коэффициент линейного расширения материала цилиндра.
Исследованию температурных напряжений в цилиндре посвящена работа [2]. Распределение температуры по толщине цилиндра описывается уравнением теплопроводности Фурье:
.                                                                  
Зависимость модуля Юнга от температуры может быть аппроксимирована полиномом:
,                                                       
где E₀ – модуль упругости бетона при нормальных условиях.
В практических расчётах вполне достаточно применения полиномов третьей степени (N=3).
Распределение флюенса нейтронов Ф вдоль стенки цилиндра определяется уравнением [3]:
,                                                              
где Ф – интегральный поток (флюенс) нейтронов; L – длина диффузии, зависящая от энергии нейтронов.
Зависимость модуля Юнга от флюенса нейтронов описывается уравнением:
,                                                           
где , , и  – эмпирические коэффициенты, зависящие от марки бетона и энергетического спектра нейтронов.
Зависимость радиационных деформаций от дозы облучения для разных описывается эмпирической формулой:
,                                                               
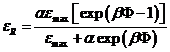где – максимальная радиационная деформация раствора (бетона) данного состава;  и – эмпирические коэффициенты, зависящие от радиационнойдеформативности заполнителя и энергетического спектра потока нейтронов.
Задача решена со следующими параметрами: r_a=3.3 м; r_b=3.8 м; T_a=300^oC; T_b=0^oC, E₀=2e4 МПа; L=0.16 м; =1; =3·10^-24 м^2/нейтр.; =0.16; =0.01; =0.7;         =10^-24 м^2/нейтр.; =0.8;
Для решения задачи был использован метод конечных разностей (МРК).
Первым этапом определялось распределение температуры в толщи цилиндра путем решения уравнения (2). Распределение температуры представлено на рис. 1.

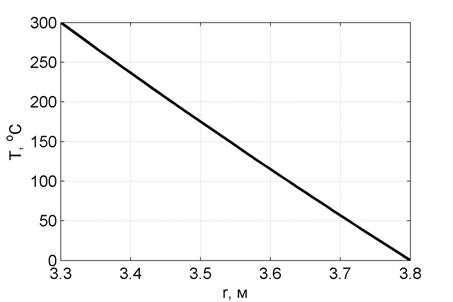
Рис. 1. График распределения температуры в толщи цилиндра

Следующим этапом, путём решения выражения (4), определялось распределение флюенса нейтронов в толщи цилиндра, которое представлено на рис. 2.

Третьим этапом определялось изменение модуля Юнга в результате температурного и радиационного воздействий. Модуль Юнга определялся по формуле:
,
где k₁ и k₂ – коэффициенты, соответствующие изменению модуля Юнга в выражениях (3) и (5).
Четвёртым этапом происходило непосредственное определение радиального и окружных напряжений в толщи цилиндра. Графики распределения напряжений представлены: радиального – на рис. 3.; окружного – на рис. 4. Сплошная линия соответствует напряжённо-деформированному состоянию с учётом изменения модуля Юнга, т.е. E=E(r); штрихпунктирная – напряжённо-деформированному состоянию без учёта изменения модуля Юнгя, т.е. E=const.

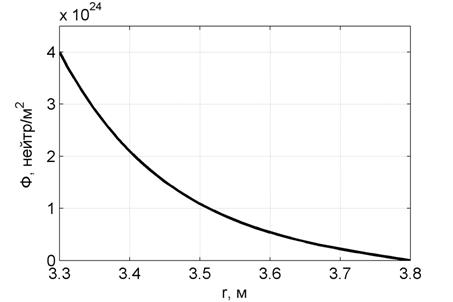
Рис. 2. График распределения флюенса нейтронов в толщи цилиндра

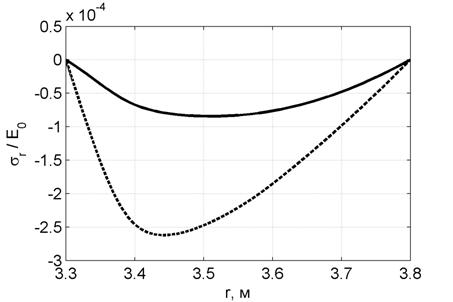
Рис. 3. График изменения радиального напряжения

Таким образом, учёт совместного влияния радиационного и температурного нагружений на величину модуля Юнга, приводит к существенным изменениям величин напряжений в толщи цилиндра по сравнению с решением, когда модуль Юнга является величиной постоянной. В частности, на внутренней грани произошло снижение окружного напряжения на 75÷80%.
Это позволяет говорить о том, что при расчёте конструкций с воздействием нескольких дополнительных нагружений (температура, радиационное воздействие и т.д.), влияющих на физико-механические параметры материала, в расчётах изменениями этих физико-механических параметров пренебрегать нельзя.

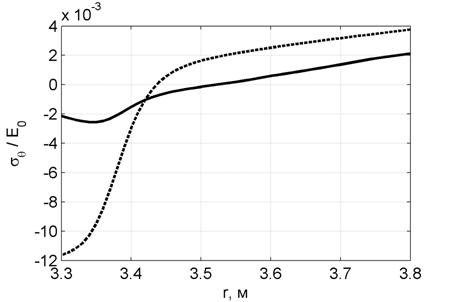
Рис. 4. График изменения окружного напряжения

Литература:
1. Андреев В.И. Некоторые задачи и методы механики неоднородных тел: Монография – М.: Издательство АСВ, 2002. – 288 стр.
2. Смолов А.В. Напряжённо-деформированнное состояние неоднородных упругих цилиндров под действием силовых и температурных нагрузок. Дис. Канд. Техн. Наук. – М.: 1987. – 161 с.
3. Дубровский В.Б. Радиационная стойкость строительных материалов. – М.: Стройиздат, 1977. – 278 с.