Анализ временных рядов киг с использованием метода фрактальной обработки

Аннотация

А.А. Резниченко, А.В. Лучинин, И.Б. Старченко

Кратко рассмотрена теоретическая модель спектра RR интервалов и ее изменения в зависимости от протекающих процессов. Изготовлено устройство для измерения кардиоинтервалограмма (КИГ). Полученные при съеме данные, различной длительности и периодичности, фиксируются для дальнейшей обработки. В ходе анализа было выявлено, что полученный спектр удовлетворяет условиям, рассматриваемым в теоретической модели, и может быть далее проанализирован с помощью фрактальных характеристик. Подобный анализ имеет большое значение при диагностике состояния пациента непосредственно в период проведения терапевтической процедуры, для ее оптимизации, как по времени, так и по интенсивности оказываемого воздействия.

Ключевые слова: КИГ; фрактальный ряд; спектр RR интервалов

05.11.17 - Приборы, системы и изделия медицинского назначения

Рассматривая организм человека, можно сказать, что он представляет из себя динамическую систему, параметры которой меняются в зависимости от целого ряда внешних факторов. Поэтому он с одной стороны достаточно хаотичен,  потому как его состояние определяется множеством внутренних факторов, но с другой стороны он действует по устойчивым закономерностям с определенной цикличностью. Так основываясь данные этих закономерностей  можно определить динамику изменений его состояния.
Для моделирования и дальнейшего исследования состояния организма, а так же выявления изменений которые произойдут в нем, в данной работе мы прибегнем к использованию фрактальной обработки сигнала. В качестве исходного сигнала будет использована КИГ. Для обработки применяется индекс фрактальности, как параметр наиболее выгодно используемый в сравнении с другими фрактальными показателями.
Наиболее известной классификацией фрактальных временных рядов является так называемая 1/f – классификация, или классификация по спектру Фурье временного ряда. Фурье-спектр хаотических временных рядов обычно описывается соотношением

A~1/fd

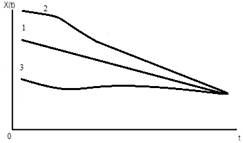
Рис. 1Теоретическое представлениеспектра RR интервалов

где А – амплитуда, f – частота, а d – показатель в зависимости от значения которого процесс относится к одному из трех принципиально различных процессов. Так если в процессе наблюдается следующие значения: d≈1 соответствует нормальному состоянию организма; d>1 характеризует перенапряжение некоторых систем или органов, а если d<1, то присутствует, соответственно, угнетение систем. И как следствие выбирается терапевтическая процедура которая сможет повлечь за собой обратный процесс (приведение к норме).
Для подтверждения вышесказанного были проведены ряд измерений, разной периодичности и длительности. Далее одному из них проведен анализ временного ряда представленный изначально сигналом следующего вида.

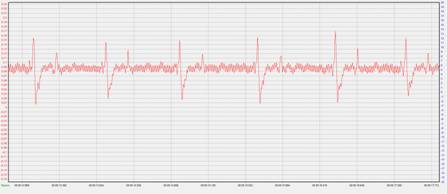
Рис. 2. Кардиоинтервалограмма, снимаемая с пациента

Дальнейшая обработка ведется на языке С++. Мы выделяем максимумы RR интервалов выше амплитуды в 0,12 В, чтобы избежать лишних шумов полученных при измерениях (при необходимости данный уровень изменяется для получения оптимального результата) и заносим их в таблицу. 

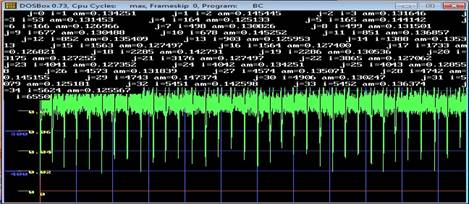
Рис. 3 представление данных программной обработки

При дальнейшей обработке полученных данных выявлено сходство с рассмотренной теоретической моделью Фурье-спектра. Так, приведенный ниже график, полученный в краткосрочном измерении, характеризует состояние организма на момент измерения.

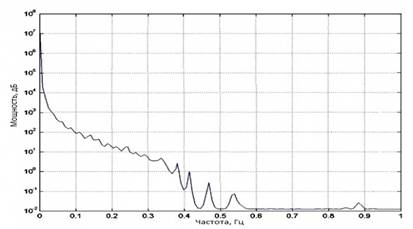
Рис. 4 – экспериментально полученный спектр RR интервалов

При подробном рассмотрении графика следует отметить, что для получения более четкой картины периодических процессов в организме следует увеличить время замера (в идеале до времени цикла). Но и при столь малом замере начинают прослеживаться некоторые из них.
Для дальнейшего анализа состояния человека потребуется смоделировать процесс фрактальной обработки полученного спектра. Было доказано, что связь  показателя d, рассмотренного в теоретической модели и наблюдаемого на практике, определенного из спектра Фурье временного ряда и показатель Херста H, определенным по значениям этого же временного ряда:
D = 2H+1
Поскольку индекс фрактальности μ связан с показателем H соотношением μ =1-H , то связь μ  и d выражается следующим образом:
D = 3 - 2μ
Так для индекса фрактальности принимающем значения 0,5< μ≤1 ,будет соответствовать розовому шуму, который характерен для рассматриваемого процесса - сердечного ритма. Теперь, зная соотношения между d, H и μ можно сформулировать поведение хаотического временного ряда. В нашем случае в  процессе существует так называемая «отрицательная» память: если в прошлом наблюдалось положительное приращение, то в будущем с высокой вероятностью будет наблюдаться отрицательное и наоборот.
Рассмотрим  временной  ряд для одной скалярной  переменной  y = f(t) ,  определенной на некотором отрезке [a,b], с использованием минимального покрытия функции f(t). Высота прямоугольника в покрытии соответственно принимает значение (t_i-1,t_i) будет равна разности между  максимальным  и  минимальным значением функции f(t) на этом отрезке. Введем величину:

где V_f(δ) – амплитудная вариация функции f(t)
Для процесса соответствующего нашему классу будим использовать следующую формулу[2]:
,
где
,
ρ(k)=exp(-1/10^k),
а ε – равномерно распределенное случайное число. Суть данной модели состоит в том, что итоговая последовательность принимает значение суммы трех периодических случайных последовательностей с различными периодами. Для моделироания требуется от трех слагаемых.
Для каждой реализации y_i=f(t) при (t_i, t_i-m) временного ряда она будет равна
V_y(δ,y_i)=b(y_i)δ^-μ(y_i)
где b(y_i) μ(y_i) константы зависящие от реализации временного ряда иот его типа. Так при большом числе реализаций наблюдается стремление параметра μ(y_i) к теоретическому значению μ, которое определяет тип ряда. Для b(y_i) будет характерно значение определяемое характеристиками приращения временного ряда. По полученным массивам значений рассчитаем следующие характеристики
<μ(t)> и < b(t)> - среднее значение μ и b
μ _min, μ _max, b _min, b _max - максимальные  и  минимальные  значения  μ и  b,  а  также величины:
;
,
характеризующие вариабельность значений μ(t) и δ(t).
Проведя описанные вычисления несколько раз, получим средние значения <μ(t)>, < b(t)>, δμ, δb по каждой реализации. Полученные в ходе анализа значения дадут представление о исследуемых фрактальных характеристиках μ и b.
По полученным данным из фрактальной обработки можно судить о поведении временных рядов. Так для каждого момента t временного  ряда  введена  функция μ(t) как значение  μ, вычисленное на минимальном, предшествующем  t интервале t_μ. Известно, что индекс μ является показателем стабильности временного ряда. Чем больше значение μ, тем стабильнее ряд.

Список литературы:

1.Алдонин Г.М. Самоорганизация в гомеостазе и донозологическая диагностика – Л.: Моделирование неравновесных систем. 1998. – 98с.
2. Шредер М. Фракталы, хаос, степенные законы. – Л.: Регулярная и хаотическая динамика. 2001. – 528с.