Линейная классификация объектов с использованием нормальных гиперплоскостей
Аннотация
Статья посвящена актуальной проблеме построения классификаторов объектов, задаваемых точками в многомерном пространстве значений признаков. Предлагается вариант геометрического разделения множеств при помощи гиперплоскостей, нормальных к межцентровому расстоянию данных множеств.Данный подход к построению разделяющих плоскостей сокращает объем выполняемых расчетных операций.
Ключевые слова: распознавание, классификация, пространство признаков, геометрический метод
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
В системах искусственного интеллекта одной из основных функций является распознавание, позволяющее соотнести исследуемый объект а к одному из ранее выделенных классов ![]() ,…
,…![]() Применение многослойных нейронных сетей для построения нелинейных классификаторов требует выполнения большого объема вычислений либо не дают приемлемого решения. В частности, метод обратного распространения ошибки не всегда дает успешные результаты при обучении многослойных сетей из-за паралича сети или попадания в локальный минимум.
Применение многослойных нейронных сетей для построения нелинейных классификаторов требует выполнения большого объема вычислений либо не дают приемлемого решения. В частности, метод обратного распространения ошибки не всегда дает успешные результаты при обучении многослойных сетей из-за паралича сети или попадания в локальный минимум.
Геометрический подход к распознаванию основан на пространственном представлении совокупности признаков {xi}, характеризующих объекты в многомерном евклидовом пространстве U. Каждому объекту а соответствует своя точка![]() . При данном способе интерпретации объектов в роли классификатора выступает одна или несколько гиперповерхностей в пространстве U, разделяющих множества точек в U, соответствующие заданным классам
. При данном способе интерпретации объектов в роли классификатора выступает одна или несколько гиперповерхностей в пространстве U, разделяющих множества точек в U, соответствующие заданным классам![]() ,…
,…![]() .Рассмотрим использование нормальных разделяющих гиперплоскостей на примере пары классов.
.Рассмотрим использование нормальных разделяющих гиперплоскостей на примере пары классов.
Обозначим координаты центров тяжести классов ![]() , через
, через ![]() и
и ![]() , радиусы их (расстояния от центра до максимально удаленной точки) - через R1, R2, Межцентровым назовем вектор
, радиусы их (расстояния от центра до максимально удаленной точки) - через R1, R2, Межцентровым назовем вектор![]() , соединяющий центры
, соединяющий центры![]() и
и![]() . По определению
. По определению![]() . Длину вектора
. Длину вектора![]() обозначим r12 и назовем межцентровым расстоянием множеств
обозначим r12 и назовем межцентровым расстоянием множеств![]() ,.Для упрощения построения разделяющих гиперповерхностей в пространстве U предложено использовать гиперплоскости, нормальные к вектору
,.Для упрощения построения разделяющих гиперповерхностей в пространстве U предложено использовать гиперплоскости, нормальные к вектору![]() . Для краткости они названы нормальными. Уравнение нормальной плоскости имеет простой вид:
. Для краткости они названы нормальными. Уравнение нормальной плоскости имеет простой вид:
![]() (1)
(1)
Основной геометрический смысл нормальных гиперплоскостей в том, что при наличии линейной разделимости классов![]() ,
,![]() , ориентация соответствующей гиперплоскости-классификатора Г12 относительно осей пространства U близка к ориентации осей у нормальных гиперплоскостей
, ориентация соответствующей гиперплоскости-классификатора Г12 относительно осей пространства U близка к ориентации осей у нормальных гиперплоскостей![]() .Нормально разделимыми назовем такую пару классов
.Нормально разделимыми назовем такую пару классов ![]() ,
,![]() для которых существует нормальная разделяющая их гиперплоскость. Данный вид является частным случаем линейной разделимости.
для которых существует нормальная разделяющая их гиперплоскость. Данный вид является частным случаем линейной разделимости.
Фактически, единственным управляемым параметром плоскости является ее свободный коэффициент ![]() . Обозначим через
. Обозначим через![]() точку пересечения нормальной плоскости с межцентровым вектором
точку пересечения нормальной плоскости с межцентровым вектором![]() , приложенным в точке
, приложенным в точке![]() . Связь
. Связь ![]() и
и ![]() следующая:.
следующая:.![]()
Для определенности будем считать, что условием разделения для точек классов А1 и А2 является следующая пара неравенств:
![]() , если
, если ![]() ,
,
![]() , если
, если ![]() . (2)
. (2)
Соответственно, два класса![]() , будем называть нормально разделимыми, если для них существует разделяющая их нормальная гиперплоскость. Доказаны две теоремы, описывающие условия существования нормальной разделимости классов в многомерном пространстве признаков.
, будем называть нормально разделимыми, если для них существует разделяющая их нормальная гиперплоскость. Доказаны две теоремы, описывающие условия существования нормальной разделимости классов в многомерном пространстве признаков.
Теорема 1. Если для классов![]() , имеющих радиусы
, имеющих радиусы ![]() , а также межцентровое расстояние
, а также межцентровое расстояние ![]() , выполняется условие
, выполняется условие
![]() (3)
(3)
то данные классы нормально разделимы и, в частности, классификатором будет являться нормальная гиперплоскость![]() , у которой свободный коэффициент
, у которой свободный коэффициент ![]() принимает следующее значение:
принимает следующее значение:
![]() ,
,
![]() . (4)
. (4)
Формула (4) задает положение точки ![]() на межцентровом векторе пропорционально радиусам разделяемых множеств.
на межцентровом векторе пропорционально радиусам разделяемых множеств.
Теорема 1 задает простейшее по форме достаточное, но не являющееся необходимым условие нормальной разделимости классов. Его преимуществом является то, что в нем не требуется дополнительно рассматривать отдельные точки классов А1 и А2. Для краткости вариант разделимости, при котором удовлетворяется условие (3), назовем шаровым.
Пример 1. Рассмотрим в двухмерном пространстве признаков {x1,x2} множества точек ![]() и
и![]() (рис.1).
(рис.1).
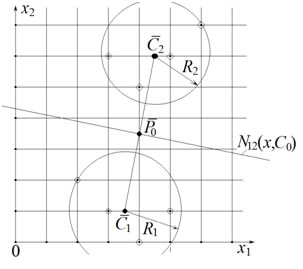
Рис. 1. - Множества точек в двухмерном пространстве признаков.
Координаты центров тяжести, радиусы множеств, межцентровый вектор и межцентровое расстояние следующие:![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Условие (3) выполняется: 1,80 + 1,80 < 5,09 . Следовательно, шаровая разделимость существует. Координаты точки
. Условие (3) выполняется: 1,80 + 1,80 < 5,09 . Следовательно, шаровая разделимость существует. Координаты точки ![]() и свободный коэффициент
и свободный коэффициент ![]() разделяющей нормальной прямой:
разделяющей нормальной прямой:
![]() ,
, ![]() .
.
Уравнение разделяющей нормальной прямой![]() :
:![]() .
.
Если форма множеств точек и значительно отличается от шаровой (они являются существенно вытянутыми вдоль одной или нескольких пространственных осей), то нормальная разделимость у классов А1,А2 может присутствовать и при значительном нарушении условия Теоремы 1. Изучение этого случая нормальной разделимости требует дополнительного исследования отдельных точек классов.
Для быстрой проверки возможного отсутствия нормальной разделимости классов предложено использовать набор простых условий.
Допустим, для классов ![]() с межцентровым вектором
с межцентровым вектором![]() и межцентровым расстоянием
и межцентровым расстоянием![]() построена нормальная плоскость, которая не является разделяющей. При этом нарушается либо только одно из условий разделимости (2) либо одновременно оба.
построена нормальная плоскость, которая не является разделяющей. При этом нарушается либо только одно из условий разделимости (2) либо одновременно оба.
Обозначим через ![]() максимально удаленную от
максимально удаленную от![]() , в которой нарушается условие разделения (2) для точек
, в которой нарушается условие разделения (2) для точек ![]() , т.е.
, т.е. ![]() и модуль
и модуль ![]() максимален. Если для данных точек нарушения нет (у всех
максимален. Если для данных точек нарушения нет (у всех![]() )), то принимаем в качестве
)), то принимаем в качестве ![]() такую точку, в которой модуль
такую точку, в которой модуль ![]() ,минимален.
,минимален.
Аналогично через ![]() обозначим максимально удаленную от
обозначим максимально удаленную от ![]() точку, в которой нарушается условие разделения (2) для точек
точку, в которой нарушается условие разделения (2) для точек![]()
Для нее ![]() и величина
и величина ![]() максимальна. Если для точек
максимальна. Если для точек ![]() нарушения условия разделимости нет (у всех
нарушения условия разделимости нет (у всех![]() ), то принимаем в качестве
), то принимаем в качестве![]() такую точку, в которой модуль
такую точку, в которой модуль ![]() минимален.
минимален.
Для исследования более сложных случаев нормальной разделимости введем вспомогательные понятия.
Рассмотрим плоскость![]() , проходящую через точку
, проходящую через точку![]() перпендикулярно вектору
перпендикулярно вектору![]() Уравнение для координат любой точки
Уравнение для координат любой точки ![]() плоскости π, можно задать в виде неявной зависимости вида:
плоскости π, можно задать в виде неявной зависимости вида:![]()
Данную функцию можно также использовать для определения расстояния от произвольной точки![]() до плоскости
до плоскости![]() :
: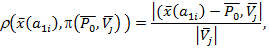
где ![]() - длина вектора
- длина вектора ![]() .
.
Позицией точки![]() из класса А1 c центром С1относительно плоскости
из класса А1 c центром С1относительно плоскости![]() назовем величину
назовем величину 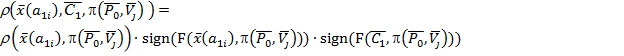 . (5)
. (5)
Смысл введенного понятия в том, что если точка ![]() и центр
и центр![]() множества А1 лежат по одну сторону от плоскости π то позиция положительна. Если они лежат по разные стороны, то величина позиции отрицательна. Так как нормальным вектором к нормальной плоскости π для множества
множества А1 лежат по одну сторону от плоскости π то позиция положительна. Если они лежат по разные стороны, то величина позиции отрицательна. Так как нормальным вектором к нормальной плоскости π для множества ![]() принимают
принимают![]() , а для А2 -
, а для А2 -![]() , то практические формулы для расчета позиций точек множеств А1 и А2 принимают следующий вид:
, то практические формулы для расчета позиций точек множеств А1 и А2 принимают следующий вид:
а)![]() ,
, ![]()
б)![]() ,
, ![]()
Позицией множества ![]() c центром
c центром![]() относительно плоскости
относительно плоскости ![]() назовем величину
назовем величину ![]() где
где![]() .
.
При анализе нормальной разделимости множеств ![]() и
и ![]() в качестве нормального вектора плоскости
в качестве нормального вектора плоскости![]() примем межцентровый вектор
примем межцентровый вектор ![]() и на нем же будем рассматривать начальные точки плоскости
и на нем же будем рассматривать начальные точки плоскости![]() .
.
Критерий нормальной разделимости для классов![]() ,
,![]() , можно задать в следующей форме.
, можно задать в следующей форме.
Теорема 2. Классы ![]() ,
,![]() , с межцентровым вектором
, с межцентровым вектором![]() нормально разделимы тогда и только тогда, когда относительно какой-либо опорной нормальной плоскости
нормально разделимы тогда и только тогда, когда относительно какой-либо опорной нормальной плоскости ![]()
для их позиций ![]()
![]() выполняется условие:
выполняется условие:![]() (6)
(6)
В частности, в качестве нормально разделяющей плоскости ![]() может быть принята плоскость, полученная сдвигом
может быть принята плоскость, полученная сдвигом ![]() точки
точки![]() по вектору
по вектору![]() :,
:,
![]()
новой точкой ![]() и свободным параметром
и свободным параметром![]() :
:![]()
Доказательство теоремы не составляет большого труда. При доказательстве достаточности, в частности, несложно показать, что в тех случаях, когда опорная нормальная плоскость![]() не является разделяющей (а)
не является разделяющей (а)![]() ,
, ![]() ;
; ![]() ;
;
б)![]() ,
, ![]() ;
;![]() то соответствующую разделяющую плоскость можно получить, задавая ее точке пересечения с межцентровым вектором смещение, равное
то соответствующую разделяющую плоскость можно получить, задавая ее точке пересечения с межцентровым вектором смещение, равное ![]() (в случае а)) и
(в случае а)) и![]() (в случае б)). В качестве опорной плоскости в Теореме 2 удобнее всего использовать нормальную плоскость, используемую в Теореме 1.
(в случае б)). В качестве опорной плоскости в Теореме 2 удобнее всего использовать нормальную плоскость, используемую в Теореме 1.
Пример 2. Рассмотрим в двухмерном пространстве признаков {x1,x2} множество точек А1 ={(1,2);(2,1);(4,1);(5,2)} и А2 = {(2,3);(3,3);(4,4)} (рис.2).
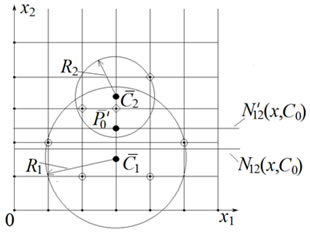
Рис.2. - Множества точек в двухмерном пространстве признаков.
Координаты центров тяжести, радиусы множеств, межцентровой вектор и межцентровое расстояние следующие:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() .
.
Условие (3) не выполняется: 2,06 + 1,20 > 1,83. Следовательно, шаровой разделимости не существует. Проверим выполнение условий Теоремы 2. Координаты точки Р0 и свободный коэффициент С0 опорной нормальной прямой:
![]()
![]() .
.
Примем в качестве опорной прямой ![]() линию:
линию:
![]()
Позиции точек множества ![]()
относительно опорной прямой равны: -0,20; 0,80; 0,80, -0,20. Позиция множества относительно опорной плоскости равна .
Позиции точек множества относительно опорной прямой равны: 1,20; 1,20; 2,20.Позиция множества ![]() относительно опорной плоскости
относительно опорной плоскости
![]() равна
равна ![]()
Условия Теоремы 2 выполняются: -0,20+1,20 = 1,00 > 0. Рассчитываем смещение![]() по межцентровому вектору, новое положение точки
по межцентровому вектору, новое положение точки![]() и новое значение свободного параметра разделяющей прямой
и новое значение свободного параметра разделяющей прямой![]()
:![]() ;
;
![]() 0;1,83)/1,83= (3; 2,43);
0;1,83)/1,83= (3; 2,43);
![]() .
.
Уравнение нормальной разделяющей линии имеет вид:![]() .
.
После сокращения на 0,83 данное уравнение принимает вид:
![]() .
.
Принцип линейной нормальной классификации объектов в многомерных пространствах признаков может быть использован для построения классификаторов для нелинейно разделимых множеств, более эффективных в плане сложности вычислений по сравнению с многослойными нейросетями.
Список литературы:
- Каллан Р. Основные концепции нейронных сетей = The Essence of Neural Networks First Edition. — 1-е. // «Вильямс», 2001. — С. 288.
- Комарцова Л. Г., Максимов А. В. Нейрокомпьютеры. — 1-е. // Изд-во МГТУ им. Н.Э. Баумана, 2002. — С. 320.
- Круглов В. В., Борисов В. В. Искусственные нейронные сети. Теория и практика.// Телеком, 2001. — С. 382.
- Патрик Э. Основы теории распознавания образов. // Сов. радио, 1980.
- Ясницкий Л.Н. Введение в искусственный интеллект. — 1-е. // Издательский центр «Академия», 2005. — С. 176.