О вычислении спрэда для обобщённой модели (B,S)-рынка в случае скупки акций
Аннотация
В этой статье представлен метод вычисления спрэда для обобщённой модели (B,S)-рынка в случае скупки акций. Приводится краткое описание актуальности и постановка задач, связанных с вычислением стоимостей производных рыночных активов и сопутствующих расчётов. Обосновывается применение мартингальной идеологии в исследованиях финансовых рынков. Излагается сущность обобщённой модели (B,S)-рынка в случае скупки акций, а также принципы расчётов верхних и нижних стоимостей опциона-колл европейского типа.
Ключевые слова: финансовый рынок, опцион, спрэд, модель, полнота, арбитраж, финансовая стратегия, модель Кокса-Росса-Рубинштейна, финансовое обязательство, мартингал
05.13.18 - Математическое моделирование, численные методы и комплексы программ
В настоящее время наблюдается рост интереса как к национальному, так и к мировому финансовым рынкам. Российский рынок ценных бумаг не является настолько развитым, чтобы можно было говорить о его сравнении с иностранными рынками. Однако, его продвижение к стандартам международного рынка, чтобы максимально быстро влиться и составить полноценную его часть, входит как в государственные интересы, поскольку увеличит инвестиции в экономику, так и в интересы международных агентов, так как упростит многие процедуры, связанные с организацией и управлением представительств в России и повысит эффективность их создания.
Международное значение России и интенсивность ее контактов в экономике и культуре будут в решающей степени зависеть от внедрения современных коммуникационных технологий, а также новых инструментов и темпов развития денежного, товарного, валютного и фондового рынков. Один из таких инструментов – опцион, имеющий особое значение на российском фондовом рынке, где показатели риска (волатильности) высоки, что характеризует рынок в целом как нестабильный.
Опцион (option; выбор) – это ценная бумага (контракт), выпускаемая фирмами, корпорациями, банками и другими финансовыми институтами и дающая покупателю право цене купить (опцион «колл») или продать (опцион «пут») определенную ценность (например, акцию, облигацию, валюту) в установленный период или момент времени на заранее оговариваемых условиях. Лицо, которое получило опцион и таким образом приняло решение, называется покупателем опциона, который должен платить за это право. Лицо, которое продало опцион, и отвечающее на решение покупателя, называется продавцом опциона.
Очевидно, что продавец и покупатель опциона преследуют разные цели, назначая, соответственно, продажную 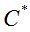 и покупную
и покупную 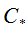 цены опциона. Современное состояние финансовых рынков позволяет охарактеризовать их как арбитражные, что приводит к появлению ненулевой разницы
цены опциона. Современное состояние финансовых рынков позволяет охарактеризовать их как арбитражные, что приводит к появлению ненулевой разницы 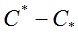 , называемой спрэдом. Спрэд является важной характеристикой состояния рынка, так как положительно коррелирован с волатильностью цен.
, называемой спрэдом. Спрэд является важной характеристикой состояния рынка, так как положительно коррелирован с волатильностью цен.
В инвестиционной политике понятие спрэда связано с построением финансовой стратегии, формирующейся за счет одновременной продажи и (или) покупки нескольких опционов. Спрэд – это портфель опционов, состоящий из опционов одного вида на одни и те же активы, но с разными ценами исполнения и (или) датами истечения. Такие стратегии считаются наиболее интересными и приносящими прибыль с наименьшим риском. Но для этого, конечно, необходимо провести анализ и расчёт в зависимости от состояния рынка и целей инвестора.
Спрэд подразделяется на вертикальный (цилиндрический, или денежный), горизонтальный (календарный, или временной) и диагональный. Вертикальный спрэд объединяет опционы с одной и той же датой истечения контрактов, но различными ценами исполнения. Горизонтальный спрэд состоит из опционов с одинаковыми ценами исполнения, но различными датами истечения контрактов. Диагональный спрэд строится на основе опционов с различными ценами исполнения и сроками истечения контрактов. Когда спрэд формируется на базе опционов, которые имеют противоположные позиции по сравнению со стандартным сочетанием, его именуют обратным спрэдом.
Математические исследования финансовых рынков ((B,S)-рынков) связаны в первую очередь с моделированием. Причём наличие риска вызывает необходимость построения стохастических моделей. Основой для анализа различных стохастических моделей (B,S)-рынка является предположение о наличии мартингальной меры , относительно которой процесс
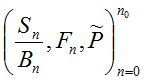 , где
, где 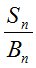 – дисконтированная цена акции, а
– дисконтированная цена акции, а 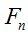 – фильтрация, является мартингалом. Основные теоремы финансовой математики устанавливают связь между экономическими состояниями финансового рынка и наличием и единственностью мартингальной меры [1].
– фильтрация, является мартингалом. Основные теоремы финансовой математики устанавливают связь между экономическими состояниями финансового рынка и наличием и единственностью мартингальной меры [1].
В работах [2,3] была разработана и исследована обобщённая модель финансового рынка типа Кокса-Росса-Рубинштейна в случае скупки акций, описывающая ситуацию, когда рынок подвержен целенаправленной скупке, то есть на нём действует агрессивный скупщик, желающий завладеть определённым количеством акций, например, контрольным пакетом. Такая ситуация вполне адекватно отражает состояние современных финансовых рынков, особенно российских, и впервые попытка исследовать рынок в случае скупки акций была предпринята в работах [4,5], где была разработана и исследована модель в случае жёсткой скупки акций. Дальнейшее развитие исследование этого состояния финансового рынка было успешно продолжено в работах [6,7]
В обобщённой модели (B,S)-рынка разделены моменты объявления новых цен на рыночные активы и моменты действий на рынке. Предполагается, что на фондовой бирже новые цены на акции объявляются в чётные моменты времени 0,2,4,6,..., в то время, как скупка акций может происходить в «промежуточные» нечётные времена 1,3,5,..., то есть в промежутках времени между объявлением цен на акции. Причём, если акция не была скуплена и продолжает эволюционировать на рынке, то изменение её стоимости имеет двойственный характер – относительное повышение, либо понижение, что соответствует концепции рынка типа Кокса-Росса-Рубинштейна. В случае, когда акция приобретается скупщиком, на рынок она больше не попадает и цена её, начиная с этого момента, эволюционирует как банковский счёт. Финальный момент исследований этой модели и, в частности, момент исполнения опциона, всегда чётный 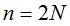 .
.
Дискретная составляющая этой модели позволила получить реальные формулы для расчётов. С точки зрения финансовой математики 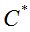 является верхней ценой контракта, а
является верхней ценой контракта, а 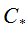 – нижней ценой. Известно [8], что
– нижней ценой. Известно [8], что
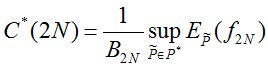 ,
,
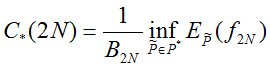 ,
,
где 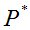 – множество мартингальных мер, а
– множество мартингальных мер, а 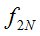 – финансовое обязательство.
– финансовое обязательство.
Таким образом, 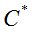 и
и 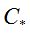 можно вычислить полным перебором по двоичным последовательностям из
можно вычислить полным перебором по двоичным последовательностям из 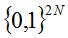 для небольших значений финального момента времени
для небольших значений финального момента времени 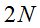 , рассчитав цену финансового обязательства по каждой такой последовательности по формуле:
, рассчитав цену финансового обязательства по каждой такой последовательности по формуле:
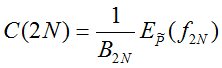
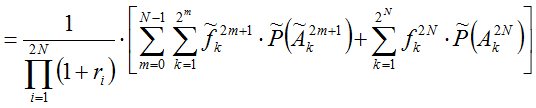 ,
,
где значения 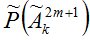 и
и 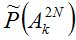 соответствующей мартингальной меры вычисляются по рекуррентным формулам [9]. Затем находится разность между максимальной и минимальной ценами финансовых обязательств, которая и является спрэдом.
соответствующей мартингальной меры вычисляются по рекуррентным формулам [9]. Затем находится разность между максимальной и минимальной ценами финансовых обязательств, которая и является спрэдом.
Результаты вычислений спрэда для Европейского опциона купли для совпадающих значений текущей стоимости акции и контрактной ценах – наиболее распространённой ситуации на рынке, и равных 1000 у.е. с разными значениями параметров рынка и для разных временных промежутков приведены в таблице №1.
Таблица №1
Вычисление спрэда
| 2N | a | b | r1 | r2 | r3 | r4 | r5 | r6 | r7 | r8 | r9 | r10 | C*, у.е. | C*, у.е. | Спрэд, у.е. |
| 10 | -0,03 | 0,03 | 0 | 0,01 | 0 | 0,015 | 0 | 0,02 | 0 | 0,017 | 0 | 0,023 | 84,2333 | 80,7887 | 3,444561 |
| 10 | -0,3 | 0,3 | 0 | 0,11 | 0 | 0,21 | 0 | 0,09 | 0 | 0,15 | 0 | 0,2 | 534,258 | 505,569 | 28,68856 |
| 10 | -0,03 | 0,03 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 96,4919 | 94,7437 | 1,748224 |
| 6 | 0,01 | 0,025 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 | 6,76301 | 6,76301 | 1,57E-07 | ||||
| 10 | -0,03 | 0,03 | 0 | 0,01 | 0 | 0,015 | 0 | 0,013 | 0 | 0,018 | 0 | 0,02 | 76,8515 | 72,6275 | 4,224 |
| 10 | -0,3 | 0,3 | 0 | 0,1 | 0 | 0,15 | 0 | 0,11 | 0 | 0,23 | 0 | 0,2 | 544,615 | 517,948 | 26,66621 |
| 10 | -0,2 | 0,4 | 0 | 0,1 | 0 | 0,2 | 0 | 0,21 | 0 | 0,15 | 0 | 0,3 | 602,309 | 581,207 | 21,10175 |
| 10 | -0,02 | 0,04 | 0 | 0,01 | 0 | 0,012 | 0 | 0,02 | 0 | 0,017 | 0 | 0,023 | 83,438 | 78,0628 | 5,375139 |
| 8 | -0,2 | 0,3 | 0 | 0,1 | 0 | 0,14 | 0 | 0,24 | 0 | 0,12 | 456,437 | 425,801 | 30,636 | ||
| 8 | -0,03 | 0,03 | 0 | 0,016 | 0 | 0,014 | 0 | 0,021 | 0 | 0,01 | 63,8836 | 58,7393 | 5,144322 |
Литература
-
Ширяев А.Н. Основы стохастической финансовой математики. Т.1 // М.:.ФАЗИС, 1998. С.529-611.
-
Красий Н.П., Павлов И.В. Модели (B,S)-рынков типа Кокса–Росса–Рубинштейна в случае скупки акций // Изв. вузов. Северо-Кавказский регион. Естеств. науки 2001. №1. С.7-11.
-
Красий Н.П., Павлов И.В. Обобщённая модель эволюции цен акций в случае их скупки // Изв. РГСУ, 2000. №5. С.165-173.
-
Белявский Г.И., Мисюра В.В., Павлов И.В. Ранговый критерий полноты одного финансового рынка при допущении арбитража // Обозрение прикладной и промышленной математики. Т.6, вып.1, 1999 г.
-
Мисюра В.В. Расчет хеджирующих стратегий для опционов европейского типа в случае (B,S)-рынка относительно специальной хааровской фильтрации // Сборник научных трудов III Всероссийского симпозима «Математическое моделирование и компьютерные технологии». Т.4., 1999 г.
-
Богачёва М.Н. Расчет цен и хеджирование опционов американского типа относительно специальной хааровской фильтрации // Обозрение прикладной и промышленной математики, Москва, ТВП. 2000, т.7, вып.2, с.477-478.
-
Богачёва М.Н., Павлов И.В. О хааровских расширениях безарбитражных финансовых рынков до безарбитражных и полных // Успехи матем. наук, 2002, т.57, в.3, с.143-144.
-
Мельников А.В., Нечаев М.Л. К вопросу о хеджировании платёжных обязательств в среднеквадратичном. // Теория вероятностей и её применения. 1998. Т.43. №1. С.672-691.
-
Красий Н.П., Павлов И.В. О безарбитражности и полноте обобщённой модели финансового рынка в случае скупки акций. // Обозрение прикладной и промышленной математики. Москва, ТВП. 1999. Т.6. №1. С.162-163.