Синтез энергоэффективных алгоритмов управления движением электропоезда в условиях преодоления неоднородностей профиля пути
Аннотация
Дата поступления статьи: 29.11.2013Рассматривается задача повышения энергоэффективности движения электропоезда при преодолении криволинейного участка профиля пути. В работе проведен синтез алгоритмов управления движением, позволяющих экономить энергетические ресурсы по средствам изменения характера движения электропоезда в зависимости от профиля пути. Проведенное моделирование движения электроподвижного состава по предлогаемой модели продемонстрировало снижение потребления энергии в сравнении с номинальным режимом.
Ключевые слова: энергоэффективность, электропоезд, управление движением, алгоритмы управления движением, снижение потребления энергетических ресурсов
05.02.02 - Машиноведение, системы приводов и детали машин
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
Повышение энергоэффективности железной дороги является актуальной задачей в настоящее время, что связано с развитием теоретической и технической базы, позволяющей внедрять в процесс управления движением электроподвижного состава новые алгоритмы и методы. В работе [1] рассмотрены различные вариации профиля пути, предложены модели экономичного движения электропоезда и сделан вывод о энергоэффективности таких моделей на численном примере. Проведем моделирование движения электропоезда по этим моделям на примере одного из профилей и определим энергетический эффект от использования планирования движения такого типа.
Согласно [2] при прохождении криволинейных планов для снижения энергопотребления необходимо изменять мгновенную скорость, поддерживая среднюю скорость постоянной. На рис. 1 представлен рассматриваемый профиль пути.
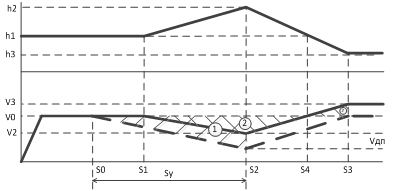
Рисунок 1 – Профиль пути 1
В соответствии с [2] необходимо разогнать поезд до подъема до скорости, достаточной для преодоления вершины пути и разгона до скорости 
под действием потенциальной энергией при движении на участке S2-S3. Если выполнено 
, то необходимо понизить скорость поезда для того, чтобы скорость в точке S3 была приближена к V0.
Из [2] мы знаем следующие выражения:
(10)
(12)
Таким образом, для достижения большей энергоэффективности при прохождении электропоездом профиля пути 1, он должен начать торможение на расстоянии Sy с ускорением α. Для построения системы управления, обеспечивающей такой закон управления, необходимо синтезировать регулятор. Для описания движения поезда воспользуемся упрощённой моделью электропоезда, описывающей механическую часть. Данная модель может быть представлена в виде дифференциальных уравнений (13) [3,7, 10]:
где m – масса локомотива, iz – передаточное число, x – положение локомотива, 
– характеристика сцепления, g – ускорение свободного падения, 
– коэффициент трения качения, Mдвj – момент, развиваемый двигателем, Rk – радиус колес, 
– угол уклона профиля.
Для синтеза регулятора, управляющего моментом тягового электродвигателя, воспользуемся методом структурного синтеза [4,5,9]. Для выполнения цели управления введем в рассмотрение ошибку регулирования:
(14)
где vт – требуемая скорость локомотива. Эта скорость формируется из начальной скорости, поддерживаемой на вертикальном участке профиля, и учитывает ускорение α, при приближении к криволинейному участку.
В соответствии с [6,8] введем в рассмотрение следующее уравнение, обеспечивающее асимптотическую устойчивость заданного состояния:
(15)
где a - константа, определяющая время переходного процесса.
Скорость локомотива выразим как:
(16)
Воспользовавшись моделью (13) и выражениями (14) – (16) получим уравнение для регулятора:
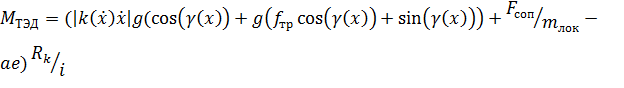(17)
(18)
Применим следующие параметры профиля: S1=2000 м, S2=3000 м, S3=4000 м, h1=3 м, h2=6 м, h3=0, номинальная скорость v0=20 м/с, промоделируем движение электропоезда вдоль рассматриваемого профиля. Рассмотрим два случая движения и сравним их. В первом случае электропоезд движется с постоянной скорость на протяжении всего пути (рис.1), во втором, он движется, используя представленную выше модель (рис.2).
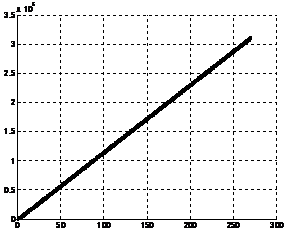
а) b)
Рис. 2 – движение с постоянной скоростью: a) график изменение скорости от времени vлок(t) b) график изменения работы тягового электродвиготеля от времени P(t)
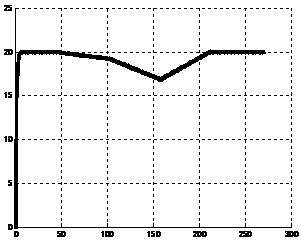
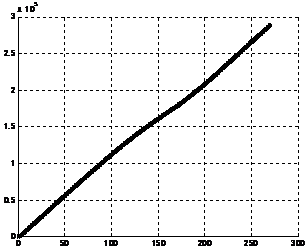
Рис. 2 – движение с переменной скоростью: a) график изменение скорости от времени vлок(t) b) график изменения работы тягового электродвиготеля от времени P(t)
По представленным графикам видно, что использование предлагаемой модели позволяет экономить энергоресуры. Так же по графикам можно определить, что в представленном случае экономия составляет 7,08 %. Предполагается, что при использовании уточненной модели выигрыш может достигать 50%.
Литература:
- В.Х. Пшихопов, М.Ю. Медведев, А.Р. Гайдук, А.А. Зарифьян В.А. Шевченко, В.Е. Беляев. Энергосберегающее управление поездами с электрической тягой на базе комплексных математических моделей. Третья международная научно-практическая конференция «Интеллектуальные системы на транспорте». 3 – 5 апреля 2013 г., г. Санкт-Петербург, Россия. – С.136-144.
- В.Х. Пшихопов, М.Ю. Медведев, А.Р. Гайдук, В.А. Шевченко. Энергосберегающее управление электропоездом в условиях неоднородности профиля пути // Известия ЮФУ. Технические науки. – 2013. – № 3(140). – С.255-260.
- Пшихопов В.Х., Гайдук А.Р., Медведев М.Ю., Беляев В.Е., Полуянович Н.К., Волощенко Ю.П. Энергосберегающее управление тяговыми приводами электроподвижного состава // Известия ЮФУ. Технические науки. – 2013. – № 2(139). – С. 192 – 200.
- Л.М. Бойчук Синтез координирующих систем автоматического управления. – М.: Энергоатомиздат, 1991. – С.96-100.
- М.Ю. Медведев Алгоритмы адаптивного управления исполнительными приводами. // Мехатроника, автоматизация и управление. 2006, № 6. С. 17 – 22.
- Medvedev M.Y., Pshikhopov V.Kh., Robust control of nonlinear dynamic systems // Proc. of 2010 IEEE Latin-American Conference on Communications. September 14 – 17, 2010, Bogota, Colombia. ISBN: 978-1-4244-7172-0. – p.72-77.
- P. Cucala Garcia, A. Fernandes Cardador. European Railway Review, 2010, № 4, p. 46 – 50; WIT Transactions on The Built Environment, 2010, № 114. – р. 549 – 560.
- В.Х. Пшихопов, М.Ю. Медведев Алгоритмическое обеспечение робастных асимптотических наблюдателей производных [Электронный ресурс] // «Инженерный вестник Дона», 2011, №2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2011/431 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Н.А. Целигоров, Е.Н. Целигорова, Г.В. Мафура Математические модели неопределённостей систем управления и методы, используемые для их исследования [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1340 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Бахвалов Ю.А., Зарифьян А.А., Кашников В.Н., Колпахчьян П.Г., Плохов Е.М., Янов В.П., Моделирование электромеханической системы электровоза с асинхронным тяговым приводом. М.: Транспорт. – 2001. – С.133-137.