О фрактальной структуре нефтегазовых месторождений
Аннотация
Проведен конструктивный анализ решения краевой задачи для дифференциального уравнения дробного порядка, моделирующий особенности притока нефти к скважине в трещинном деформируемом пласте, а так же рассмотрены задачи описывающие процесс диффузии в пористых средах, где сильно вязкая жидкость (нефть) вытесняется слабо вязкой жидкостью водой.
Ключевые слова: Дифференциальный и интегральный операторы дробного порядка, краевая задача, вязкоупругие материалы (полимеры), фракталы.05.13.18 - Математическое моделирование, численные методы и комплексы программ
В последнее время при изучении неупорядоченных систем весьма эффективно используются фрактально – геометрические методы [1] , [2] ,основным для аппарата фрактальной математики является понятие дробной размерности, впервые введенное Хаусдорфом. На языке фрактальной математики в 1980 г. были сформулированы основные положения теории протекания. В частности, установлена фрактальная природа так называемых вязких пальцев в пористых средах, где сильно вязкая жидкость ( нефть ) вытесняется слабо вязкой жидкостью водой [ 1 ].
В работе [ 1] дается анализ фрактально – геометрических показателей в моделировании нефтегазносности и проводимости паровых коллекторов. Отмечено, что поведение нефтегазностнных коллекторов, представленных пористыми средами, в существенной мере определяется стохастическими факторами, включая хаотическое распределение зерен породы коллекторов по форме и размерам.
Электрическая проводимость пористых нефтегазосодержащих пластов, исследуемая при их электромагнитном каротаже, также имеет фрактальную структуру, характерную для перкуляционного кластера.
Фрактальные кластеры образуемые песчаными, имеют значении хаусдорфовой размерности , располагающиеся в интервале
D=2,57+2,87.
В данной работе приток жидкости к скважине в трещиноватом деформируемом пласте, производится с помощью интегродифференциальных уравнений дробного порядка. В практике разработки нефтяных залежей существуют различные зависимости дебита от перепада давления. Отклонение рассматриваемых зависимостей от линейной объясняется причинами, основными из которых являются деформация коллектора и инерционные силы сопротивления, изменение свойства пласта и жидкости.
В области больших скоростей фильтрации ( при забойной зоне пласта) нарушается линейный закон.
Существуют функциональная зависимость, учитывающая инерционные составляющего сопротивления движению жидкости [1].![]() (1)
(1)
где ![]() - градиент давления,
- градиент давления,![]() - динамическая вязкость жидкости,
- динамическая вязкость жидкости, ![]() - скорость фильтрации,
- скорость фильтрации,![]() модуль скорость фильтрации,- проницаемость среды,
модуль скорость фильтрации,- проницаемость среды, ![]() - скалярная величина, зависящая от модуля вектора скорости,
- скалярная величина, зависящая от модуля вектора скорости,![]() - безразмерная функция, полученная согласно
- безразмерная функция, полученная согласно ![]() – теореме анализа размерности.
– теореме анализа размерности.
Теорема послужила основным толчком в применении фрактального анализа в данной области, поэтому подробно приведем здесь эту исключительно важную теорему и автору кажется, что это теорема будет в дальнейшем играть центральную роль при моделировании различных процессов.
Теорема (![]() – теорема анализа размерности) [ 9].
– теорема анализа размерности) [ 9].
Если дано физически значимое выражение:![]()
где![]() — это n различных физических переменных и они выражаются через k независимых физических величин, то это выражение может быть переписано в виде:
— это n различных физических переменных и они выражаются через k независимых физических величин, то это выражение может быть переписано в виде:![]() где
где ![]() — эти безразмерные параметры, полученные из
— эти безразмерные параметры, полученные из![]() при помощи
при помощи ![]() выражений следующего вида:
выражений следующего вида:![]()
где показатели степеней![]() — эти рациональные числа.
— эти рациональные числа.
Допуская возможность разложения функции в ряд Тейлора и ограничиваясь первыми двумя членами разложения, получим
![]() (2)
(2)
Движение жидкости в чисто трещиноватом коллекторе гораздо точнее ( чем закон Дарси ) описывается двучленной зависимостью (2).
По формуле (2) первое слагаемое учитывает потери давления от трения между жидкостью и трещиноватой средой, второе – инерционную составляющую сопротивления жидкости, связанную с сужением и расширением элементарных стружек потока в трещинах, поворотами струей и т.д.
Из формулы (2) следует число при малых скоростях фильтрации квадратом модуля![]() можно пренебречь и градиент давления
можно пренебречь и градиент давления![]() будет зависеть только от первого слагаемого ( вязости жидкости
будет зависеть только от первого слагаемого ( вязости жидкости![]() , проницаемости трещин
, проницаемости трещин![]() и скорости фильтрации
и скорости фильтрации![]() ) т.е. движение будет безинерциональнным.
) т.е. движение будет безинерциональнным.
При больших скоростях фильтрации силы инерции будет преобладать над силами вязкости, поскольку в формуле (2) определяющим будет второе слагаемое. Может оказаться, что при достаточно больших скоростях фильтрации силы вязкости будут пренебрежимо малы по сравнению с силами инерции и следовательно, двучленная зависимость (2) будет зависеть в виде одночленного закона Краснопольского –Шеди, впервые установленное Краснопольским А.А. в 1912г.[ 4]
Формула (2) впервые был предложен Форхгеймером [4]. В этой работе показано, что (2) совпадает с первыми двумя членами разложения в ряд Тейлора функции![]() .
.
С ростом градиента давления изменяется фильтрационная способность коллектора.
Это может быть связанно с изменением действующей толщины пласта, которая для каждого конкретного коллектора при различных градиентах давления ![]() ( до критического значения
( до критического значения![]() ) различна. С ростом градиента давления до критического значения
) различна. С ростом градиента давления до критического значения![]() в процессе фильтрации вовлекаются все более мелкие поры.
в процессе фильтрации вовлекаются все более мелкие поры.

Рис.1 Изменение действующей мощности трещиноватого пласта
При достижении действующая толщина пласта достигает максимального значения и остается неизменной при дальнейшем увеличении градиента давления ( рис. 2)

Рис.2 Зависимость действующей толщины трещиноватого пласта от градиента давлении.
Последующие изменения могут привести к сужению некоторых фильтрационных каналов и к уменьшению действующей толщины пласта.
При расширении движения жидкости в деформируемом пласте будет считать, что толщина пласта изменяется плавно, колеблясь около среднего значения [4]. За срединную поверхность приведенного пластового давления примем горизонтальную плоскость, находящуюся на одинаковом расстоянии от кровли и подошвы. Выбирая в этой плоскости направление координатных осей Ox,Oy,Oz проинтегрировав уравнение неразрывности ![]()
по мощности пласта
![]() ,
,
получим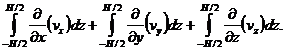 (3)
(3)
Дифференцируя интеграл по параметру, преобразуем первое слагаемое уравнения (3)
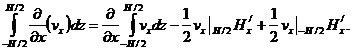
При оси ассиметрической фильтрации течение жидкости на кровле и подошве практически отсутствует, следовательно последними двумя членами в полученном равенстве можно пренебречь, т.е. 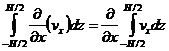 (4)
(4)
Применяя теорему о среднем к интервалу с учетом получим: 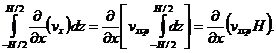 (5)
(5)
Аналогично преобразуем второй интеграл в уравнении (3) т.е.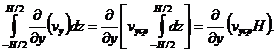 (6)
(6)
Третий интеграл в (3) равен нулю. Докажем это следующим образом.
Оценивая третий интеграл, имеем
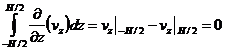 .
.
Так как![]() то
то![]() и
и ![]()
С учетом приведенных преобразований из уравнения (3) получим усредненное уравнение неразрывности:![]() (7)
(7)
Уравнение (7) описывает установившиеся течение жидкости в пласте с изменяющейся толщиной.
При выводе уравнения (7) операции индекс «ср.» правильность такой операции допустима. Далее, выразив![]() из (2), имеем
из (2), имеем ![]()
Из полученного выражения следует:
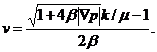 (8)
(8)
Подставим в уравнение (7) значение скорости фильтрации (8) при![]() ниже критического, т.е. при изменяющейся толщине пласта. В случае ассимитрической фильтрации в полярных координатах уравнение неразрывности запишем в виде [4].
ниже критического, т.е. при изменяющейся толщине пласта. В случае ассимитрической фильтрации в полярных координатах уравнение неразрывности запишем в виде [4].
![]() .
.
Оттуда имеем
![]()
Постоянную интегрирования![]() при условии
при условии![]() и учитывая, что W дебит скважины радиусом
и учитывая, что W дебит скважины радиусом ![]() взрывший пласт толщиной
взрывший пласт толщиной ![]() находим
находим
![]() (9)
(9)

Рис. 3 Зависимость действующей толщины пласта от градиента давления.
В промысловой практике принято считать
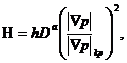
![]() (10)
(10)
где ![]() - толщина пласта при
- толщина пласта при![]() ,
,![]() - эмпирический коэффициент, характеризующий изменение действующей толщины пласта от градиента давления (рис.1). В [ 8] было предложено (10) заменить, учитывая, что фильтрация идет в одном направлении.
- эмпирический коэффициент, характеризующий изменение действующей толщины пласта от градиента давления (рис.1). В [ 8] было предложено (10) заменить, учитывая, что фильтрация идет в одном направлении.
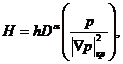
![]()
Здесь![]() - оператор дробного интегродифференцирования порядка
- оператор дробного интегродифференцирования порядка![]() в смысле Римана – Лиувилля. Из (8) и (9) следует, что
в смысле Римана – Лиувилля. Из (8) и (9) следует, что
![]()
Откуда
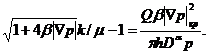 (11)
(11)
Очевидно, что
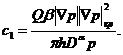
После несложных преобразований из (11) получим
![]() (12)
(12)
где
![]()
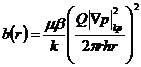
Уравнение (12) впервые предложено в работе ![]()
В начале решим уравнение (12) с помощью степенных рядов специального вида.
Представим (12) в виде
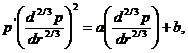 (13)
(13)
Здесь
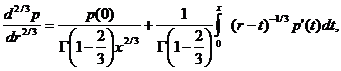 (14)
(14)
Решение уравнения 13 будем искать в виде ряда
![]()
Продифференцировав это уравнение, получаем
![]() (15)
(15)
где
![]()
Очевидно, что
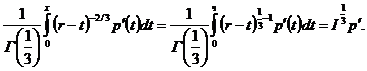
Поэтому наше уравнение (13) запишем в виде
![]()
Где
![]()
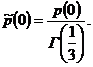
Последнее уравнение перепишем следующим образом
![]() (16).
(16).
Если ![]() то
то ![]()
Имеем
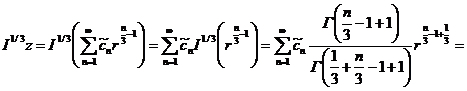
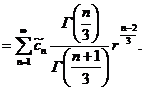
Вычислим
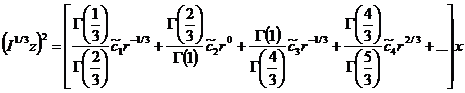
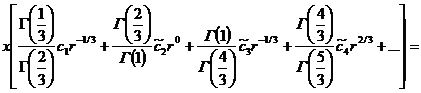
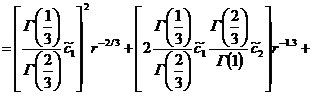
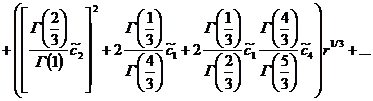
И последнее вычислим![]() , тогда получим
, тогда получим
![]()
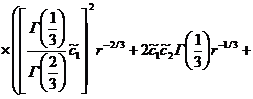
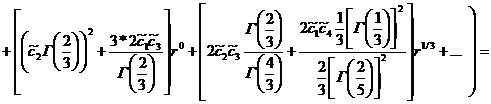
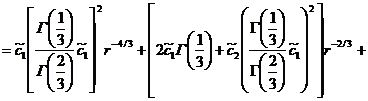
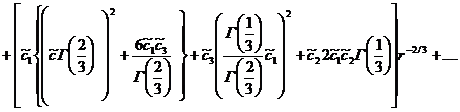
Уравнение (16) примет вид
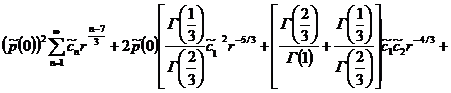
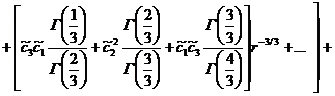
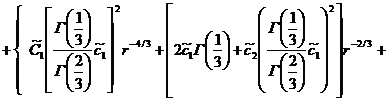
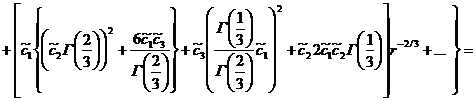
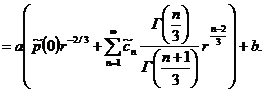
Приравнивая коэффициенты при одинаковых степенях получим:
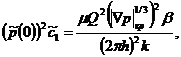
Отсюда
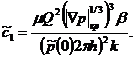
Литература
- 1.Баренблатт Г.И. Теория нестационарной фильтрации жидкости и газа. – М.: Наука, 1972 – 287с.
2.Шаймуратов Р.С. Гидродинамика нефтяного трещинного пласта. – М.: Недра, 1980 – 223с.
3.Hausdovff F., “ Math. Ann.” 1918, Bd 79, S. 157-179.
4.Krivonosov I.V. , Balakirev V.A. Development, research and expenation ofa multilayerchinks/ Nedra, Russia 1975.
5.Bulygin B.Y., Hydrdynamics of an oil eayer, Neclva, Pussia, 1974.
6.Podlubny I, Tractional differential equations, Academic press, New York 1999.
7.Джрбашян М.М. Интегральные преобразования и представления функций в комплексной области. - М.: Наука. 1966. - 677 с.
8.Алероев Т.С. Краевые задачи для дифференциальных уравнений с дробными производными. Докторская диссертация. М.: МГУ, 2000.
9.Buckingham, E. (1914). «On physically similar systems; illustrations of the use of dimensional equations». Phys. Rev. 4: 345—376.