Разработка алгоритма управления процессом адаптации нечетких проектных метаданных
Аннотация
На основе автомата адаптации разработан алгоритм, позволяющий адаптивно корректировать параметры функции принадлежности проектных данных. Корректировку параметров функции принадлежности предлагается осуществлять на основе анализа реакции проектировщика на результаты запросов. Данный подход позволяет корректировать степени принадлежности проектных решений соответствующим значениям логических переменных на основе субъективных последовательных мнений экспертов. При этом наличие механизма адаптации позволяет снижать влияние разовых, выпадающих из общей концепции, мнений.
Ключевые слова: автомат адаптации, нечеткие данные, корректировка.Ключевые слова:
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
Описание проблемной области. В качестве примера рассмотрим запрос, сформулированный на естественном языке: «Выбрать алгоритмы, решающие задачу Штейнера большой размерности с низкой погрешностью за приемлемое время». В данном запросе фигурируют одно четкое высказывание «алгоритмы, решающие задачу Штейнера» и три нечетких высказывания: «большой размерности», «с низкой погрешностью», «за приемлемое время». Четкое высказывание «алгоритмы, решающие задачу Штейнера» однозначно описывает интересующее множество алгоритмов. В свою очередь нечеткие высказывания: «большой размерности», «с низкой погрешностью», «за приемлемое время» подразумевают наличие некоторой функции принадлежности , численно характеризующей степень принадлежности, элемента к соответствующему не четкому множеству.
В случае конечного множества аргументов функция принадлежности может быть задана перечислением т.е. непосредственным указанием для каждого элемента его степени принадлежности нечеткому множеству. В качестве примера зададим нечеткую переменную «приемлемое время», определим область рассуждений переменной «приемлемое время» тремя характеристиками сложности алгоритма: линейная, полиномиальная, экспоненциальная. Принадлежность каждого элемента области рассуждений нечеткому множеству «приемлемое время» определим перечислением С={0.98/линейная,0.5/полиномиальная, 0.03/экспоненциальная}.В случае непрерывной (бесконечной) области определения, функция принадлежности чаще всего принимает треугольный или трапецеидальный вид. Треугольная функция принадлежности задается тройкой чисел (a, b, c), и ее значение в точке x вычисляется согласно выражению:
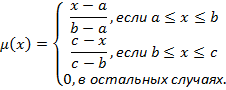 (1)
(1)
Аналогично задание трапецеидальной функции принадлежности осуществляется четверкой чисел (a, b, c, d):
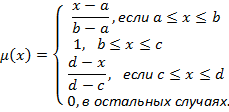 (2)
(2)
Так как треугольная функция является частным случаем трапецеидальной, рассмотрим последнею в качестве примера (рис.1)
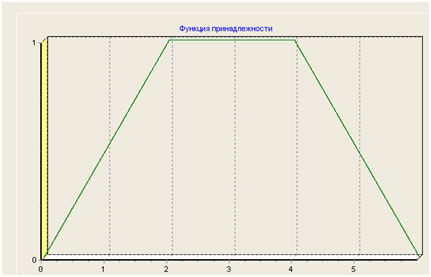
Рис. 1 Пример трапецеидальной функции принадлежности
На рис. 1 приведена функция принадлежности заданная кортежем (0, 2, 4, 6). В качестве аргументов функций (1)-(2) выступают некоторые численные характеристики объекта, для которого необходимо определить степень принадлежности к нечеткому множеству.
Высказывания «с низкой погрешностью» и «за приемлемое время»динамически стабильны в том плане что в ближайшей перспективе погрешность алгоритма равная 0,05 скорее всего будет считаться низкой, а полиномиальная временная сложность – приемлемой. Подобные рассуждения неприменимы к выражению «большой размерности» так как число элементов в проектируемых СБИС постоянно увеличивается (Гордон Мур высказал предположение, согласно которому число транзисторов на кристалле будет удваиваться каждые 24 месяца). Пусть логическая переменная «размерность задачи» принимает два значения «не большая» и «большая». Параметры функции принадлежности для каждого значения логической переменной определим кортежами: «не большая» (0,0,102,105) и «большая» (103,108,1010,1010). Графики функций принадлежности приведены на рис. 2.
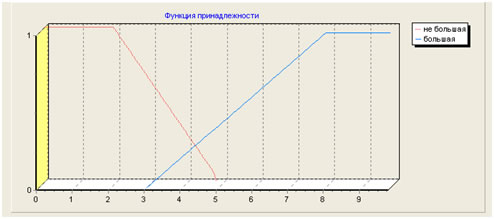
Рис. 2 Графики трапецеидальных функций принадлежности
На рис. 2 численные характеристики размерностей задач откладываются по оси абсцисс как показатели степени с основанием 10, а по оси ординат степени принадлежности задач указанной размерности к значениям «не большая» и «большая» логической переменной «размерность задачи».
Логично предположить что с течением времени параметры функции принадлежности логической переменной «размерность задачи» будут увеличиваться и данные изменения необходимо адекватно отражать. В подобных ситуациях целесообразно корректировать вершины трапеции на основе решений принимаемых экспертом-проектировщиком (ЭП) в схожих ситуациях. Для этих целей необходимо разработать систему поддержки принятия решений (СППР), например аналогичную по структуре представленной в [1].
Постановка задачи. Необходимо разработать алгоритм, позволяющий адаптивно корректировать параметры функции принадлежности. Корректировку параметров функции принадлежности предлагается осуществлять на основе анализа реакции ЭП на результаты запросов.
Предполагается,что взаимодействие ЭП и СППР состоит в следующем:
- ЭП генерирует нечеткий запрос.
- В качестве результата выполнения запроса система возвращает ЭП множество потенциальных решений.
- Если ЭП находит необходимое решение во множестве потенциальных решений - СППР приступает к анализу действий эксперта. Если же эксперт не находит требуемый ответ он может задать параметры запроса «вручную».
Логично предположить что СППР должна функционировать таким образом чтобы минимизировать необходимость «ручной» генерации запросов. По этой причине для повышения эффективности функционирования СППР необходимо разработать методы корректировки нечетких проектных метаданных (параметров функций принадлежности) хранимых в базе данных (БД) на основе анализа действий ЭП.
Предлагаемый подход основывается на корректировке параметров функции принадлежности. Решение x, хранящееся в БД, попадает во множество потенциальных решений только в том случае если![]() , где индекс соответствия решения x нечеткому высказыванию а,
, где индекс соответствия решения x нечеткому высказыванию а,![]() - минимальный индекс соответствия. Таким образом, для любого решения x из множества потенциальных решений X справедливо:
- минимальный индекс соответствия. Таким образом, для любого решения x из множества потенциальных решений X справедливо:
![]()
Из множества потенциальных решений X для дальнейшего анализа эксперт выбирает подмножество . Если выполняется условие:
![]() ,
,
где ![]() логично предположить, что необходимо скорректировать параметры функции принадлежности таким образом, чтобы несколько увеличить .
логично предположить, что необходимо скорректировать параметры функции принадлежности таким образом, чтобы несколько увеличить .
Для управления процессом корректировки нечетких данных разработан автомат адаптации (АА) схема которого приведена на рис. 4 [2,3]. Предлагаемый АА поддерживает две альтернативы A1 и A2. Состояние S11 – соответствует альтернативе A1, а состояния S21 - S23 альтернативе A2.
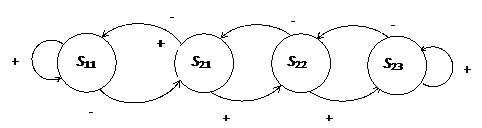
Рис. 4. Схема предлагаемого АА
Альтернатива A1 заключается в необходимости корректировать параметры функции принадлежности, а альтернатива A2 подразумевает неизменность параметров функции принадлежности. Схема выработки управляющих сигналов поощрения (+) и наказания (-) АА представлена в таблице.
Таблица. Управляющие сигналы
Отклик Альтернатива |
|
|
|
A1 |
+ |
- |
|
A2 |
- |
+ |
Данный подход позволяет увеличивать степень принадлежности потенциальных решений на основе субъективных, последовательных мнений экспертов. При этом наличие механизма адаптации позволяет снижать влияние разовых, выпадающих из общей концепции, мнений.
Литература
- 1. Бова В.В., Гладков Л.А., Кравченко Ю.А., Курейчик В.В., Курейчик В.М., Марков В.В., Нужное Е.В., Родзин С.И., Рогозов Ю.И., Свиридов А.С., Щеглов С.Н. Адаптивные и бионические методы и интеллектуальном анализе данных. - Таганрог: Изд-во ТТИ ЮФУ, 2010. - 109 с.
2.Лебедев Б.К. Методы поисковой адаптации в задачах автоматизированного проектирования СБИС: Монография. -Таганрог: Изд-во ТРТУ, 2000.
3. Лебедев Б.К. Адаптация в САПР. Монография. Таганрог: Изд-во ТРТУ, 1999. -