Измерение плотности ВЧ и СВЧ энергии методом лазерной интерференционной термометрии
Аннотация
Дата поступления статьи: 21.12.2012Изложена разработанная авторами методика измерения плотности энергии ВЧ и СВЧ поля с применением полупроводникового лазерного интерферометра, измеряющего изменение оптической толщины стеклянной пластины, помещаемой в область ВЧ или СВЧ нагрева. Работоспособность методики продемонстрирована на примере измерения распределения плотности энергии электромагнитного поля СВЧ печи.
Ключевые слова: Лазерный интерферометр, измерение температуры, датчик ВЧ и СВЧ поля
В настоящее время метод лазерной интерференционной термометрии (ЛИТ) наиболее часто (по сравнению с другими) применяется для дистанционного контроля температуры полупроводниковых и диэлектрических подложек в микроэлектронике. Метод ЛИТ имеет высокую разрешающую способность по температуре (не хуже 0,05 К) в широком диапазоне измеряемых температур [1]. Основываясь на этом методе, нами разработано и создано устройство для бесконтактного контроля мощности высокочастотного (ВЧ) или сверхвысокочастотного (СВЧ) поля, поглощенного прозрачной средой [2]. Однако в технологических процессах пищевой промышленности, в которых используется диэлектрический нагрев, обрабатываемые материалы, как правило, не прозрачны и не имеют жестких геометрических размеров. Поэтому прямое применение ЛИТ для контроля мощности, поглощенной материалами, не представляется возможным.
Необходимо отметить, что качественная обработка материала в камерах ВЧ или СВЧ нагрева допустима только в том случае, если плотность распределения энергии электромагнитного поля (ЭМП) в них практически равномерна [3]. На ВЧ это условие достаточно просто обеспечивается расчетным путем [4]. На СВЧ существуют сложности с определением типа волн, возбуждаемых в камере нагрева. Поэтому в этом диапазоне длин волн плотность ЭМП определяют экспериментально с помощью измерителя плотности потока мощности, а также СВЧ ваттметра в сочетании с измерительной антенной [5, 6].
Данная работа посвящена разработке методики, позволяющей контролировать распределение плотности энергии ВЧ или СВЧ поля с помощью разработанного нами устройства [2]. Схема этого устройства показана на рис.1.
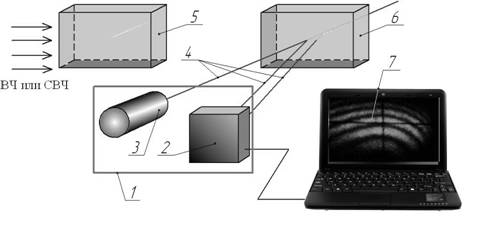
Рис. 1. Схема лазерного интерферометра: 1 – измерительный блок; 2 – видеокамера; 3 – полупроводниковый лазер; 4 – лучи лазера; 5 – датчик мощности, помещенный в камеру нагрева; 6 – тот же датчик, но за пределами камеры нагрева, 7 – монитор компьютера с изображением интерференционной картины
Датчик в форме параллелепипеда из оптически прозрачного материала с размерами много меньше длины волны электромагнитного излучения помещают в камеру СВЧ нагрева. Мощность, поглощаемая датчиком, определяется по формуле [3]:
![]() , (1)
, (1)
где w – угловая частота колебаний ЭМП, ε0 – электрическая постоянная, εr и tg δ – относительная диэлектрическая проницаемость и тангенс угла диэлектрических потерь материала датчика, E – эффективная величина напряженности электрического поля (ЭП) в материале датчика и V – объем датчика.
Мощность P расходуется на изменение температуры и энергии упругих деформаций датчика, а также на компенсацию тепловых потерь при взаимодействии датчика с окружающей средой в камере нагрева. В то же время, если датчик находится в ЭМП в течение времени, значительно меньшем постоянной времени нагрева датчика, то мощность, поглощаемую датчиком, можно определить по формуле:
![]()
![]() , (2)
, (2)
где T и T0 – температуры датчика и окружающей среды в камере нагрева, ![]() – масса датчика,
– масса датчика, ![]() – удельная теплоемкость материала датчика,
– удельная теплоемкость материала датчика, ![]() – время нагрева.
– время нагрева.
Ориентация силовых линий ЭМП зависит от типа возбуждаемой в камере электромагнитной волны [7]. Известно, что для диапазона СВЧ волн граничные условия по полю таковы, что силовые линии ЭП, примыкающие к металлическим стенкам камеры нагрева, перпендикулярны или параллельны им. Поэтому, располагая датчик на минимальном расстоянии от стенок и ориентируя его большую грань параллельно им, можно обеспечить перпендикулярность или параллельность силовых линий ЭП большим граням датчика. Если силовые линии перпендикулярны, то напряженность ЭП для точек, находящихся в воздухе около больших граней датчика, рассчитывается по формуле E0 = εrE, если линии поля параллельны, то E0 = E [8].
Прогретый в камере нагрева датчик извлекают из камеры и помещают в интерферометр. Отраженные от противоположных граней датчика пучки лазерного излучения интерферируют. Интерференционная картина регистрируется видеокамерой. В результате изменения коэффициента преломления и толщины датчика при его нагреве происходит смещение интерференционных полос. В методе ЛИТ температура датчика в процессе измерения находится так [1]:
![]() , (3)
, (3)
где λ – длина волны лазерного излучения, ΔN = |N – N0|, N и N0 – номера полос интерференции для прогретого и охлажденного до температуры воздуха в лаборатории ![]() датчика, n0 и h0 – показатель преломления материала датчика и его толщина при температуре
датчика, n0 и h0 – показатель преломления материала датчика и его толщина при температуре ![]() , β0 и β – температурные коэффициенты показателя преломления и линейного расширения материала датчика.
, β0 и β – температурные коэффициенты показателя преломления и линейного расширения материала датчика.
Приравнивая (1) и (2), учитывая (3) и зависимости между E0 и E, полагая, что T ≈ T' и ![]() , а так же выделяя из полученного равенства плотность энергии ЭМП в вакууме в соответствии с формулой w = ε0 E02, получаем
, а так же выделяя из полученного равенства плотность энергии ЭМП в вакууме в соответствии с формулой w = ε0 E02, получаем
![]() , (4)
, (4)
где ξ = εr, если силовые линии ЭП перпендикулярны большим граням датчика и ξ = 1/εr, если они параллельны, ![]() - плотность материала датчика.
- плотность материала датчика.
Отсюда следует, что плотность энергии ЭМП в пространстве камеры нагрева свободном от обрабатываемого материала пропорциональна ∆N, т.е. w ≈ K∆N. Коэффициент пропорциональности K зависит от физических свойств материала и размеров датчика, длины волны лазерного излучения, ориентации силовых линий ЭП относительно датчика, частоты колебаний генератора ВЧ или СВЧ энергии в камере нагрева. Генераторы, применяемые в промышленности, вырабатывают, как правило, высокостабильную по частоте колебаний электромагнитную энергию. Таким образом, при обеспечении постоянства коэффициента K, основные сложности определения плотности энергии будут связаны с измерением ∆N. Особенности измерения этого параметра (в том числе определение дробной части интерференционной полосы) подробно рассмотрены в статье [9], а типичная интерференционная картина, получаемая на экране компьютера, приведена на рис. 1.
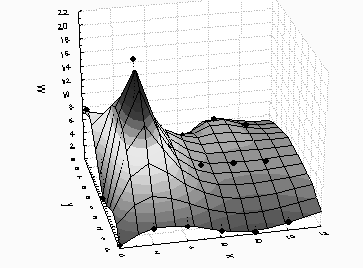
Рис. 2. Распределение плотности электромагнитной энергии на высоте 10 мм от дна камеры СВЧ печи (точки – экспериментальные значения)
Результаты исследования распределения плотности электромагнитной энергии w в камере СВЧ печи с применением полупроводникового лазера марки HLDPM12-655-25 показаны на рис. 2.
В заключение укажем, что описанный выше метод нахождения распределения плотности ЭМП можно применять в лабораторных исследованиях, а также в опытно-конструкторских работах с целью оптимизации камер ВЧ или СВЧ нагрева.
Литература
1. Магунов А.Н. Лазерная термометрия твердых тел. – М.: ФИЗМАТЛИТ, 2001. – 224 с.
2. Дородов П.В., Гусева Н.В., Киселёв М.М. Устройство для бесконтактного определения мощности СВЧ-излучения // Механизация и электрификация сельского хозяйства. – 2009. – № 6. – С. 32 – 33.
3. Рогов И.А., Некрутман С.В., Лысов Г.В. Техника сверхвысокочастотного нагрева пищевых продуктов.– М.: Легкая и пищевая промышленность, 1981. – 200 с.
4. Морозов В.А. Расчёт характеристик рабочего конденсатора с прямоугольными электродами // Электротехника. – 2002. – № 11. – С. 41 – 44.
5. Билько М.И., Томашевский А.К. Измерение мощности на СВЧ. – М.: Радио и связь, 1986. – 168 с.
6. Морозов В.А., Михеев Г.М., Зонов Р.Г. Ваттметр для высокочастотной системы с плазменной нагрузкой // Харьковская нанотехнологическая ассамблея. Том I. Вакуумные нанотехнологии и оборудование / Под общ. ред. И.М. Неклюдова, В.М. Шулаева. - Харьков: ННЦ «ХФТИ»: ИПП «Контраст», 2006. - С. 41 - 45.
7. Федоров Н.Н. Основы электродинамики: учеб. пособие для вузов. – М.: Высш. школа, 1980. - 399 с.
8. Парселл Э. Электричество и магнетизм. Пер. с англ. – М.: Наука, Глав. ред. физ.-мат. литературы, 1971. – 448 с.
9. Беркутов В.П., Гусева Н.В., Дородов П.В., Киселев М.М. Интерферометр для определения нормальных напряжений в плоских прозрачных моделях // Датчики и системы. – 2009. – № 2. – С. 26 - 29.