Разработка алгоритма нахождения максимального потока минимальной стоимости в нечеткой динамической транспортной сети
Аннотация
Дата поступления статьи: 30.03.2013Данная статья рассматривает задачу нахождения максимального потока минимальной стоимости в нечеткой динамической транспортной сети. Актуальность рассматриваемой задачи в ее широком практическом применении на сетях железных, воздушных, морских дорог при нахождении маршрутов перевозки минимальной стоимости. Особенность постановки задачи в том, что учитывается нечеткий характер таких параметров транспортной сети, как пропускные способности и стоимости перевозок, что позволяет принимать более чувствительные к изменениям окружающей среды решения. Также принимается во внимание зависимость параметров транспортной сети от времени отправления потока, что позволяет ввести понятие «динамическая» сеть в отличие от «стационарно-динамических», рассматриваемых в литературе по потокам. Предлагается алгоритм решения поставленной задачи в нечетких условиях. Для иллюстрации работы алгоритма представлен численный пример.
Ключевые слова: динамическая транспорная сеть, максимальный поток минимальной стоимости, нечеткие числа, пропускная стособность, время прохождения потока
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Введение
Задачи, рассматриваемые на транспортных сетях, в частности, потоковые задачи являются актуальными, поскольку позволяют решать широкий круг практических задач, а именно, задач нахождения максимального количества потока, которое можно передать по дугам сети, нахождения минимального по стоимости маршрута перевозки заданного количества единиц товара и пр. Потоковые задачи нахождения максимального потока и потока минимальной стоимости в транспортных сетях широко освещались в литературе авторами [1, 2, 3]. Но в условиях реальной жизни в данных задачах необходимо учитывать, что такие параметры транспортных сетей, как пропускные способности и стоимости перевозок не могут быть точно известны. На данные параметры влияют различные экзогенные и эндогенные виды неопределенности [4], в частности, пробки на дорогах, ремонтные работы, колебания в ценах на бензин, следовательно, мы приходим к потоковым задачам в транспортных сетях в нечетких условиях [5]. Данная область является менее исследованной, подобные задачи были рассмотрены в [6].
Потовые задачи, описанные ранее, можно отнести к статическим, так как при их рассмотрении не учитывается параметр времени прохождения потока по дугам сети. В действительности, поток затрачивает определенное время, чтобы добраться от начальной вершины дуги к конечной. Следовательно, мы приходим к «стационарно-динамическим» задачам. Данные модели предполагают не мгновенное прохождение потока по дугам сети. Данные задачи рассматривались в литературе авторами [1, 7].
Рассматриваемые в литературе задачи на динамических сетях, которые мы будем называть «стационарно-динамическими» задачами учитывают не мгновенное прохождение потока по дугам сети и не принимают во внимание возможность параметров транспортных сетей меняться во времени. Действительно, пропускные способности, стоимости перевозок и параметры времени прохождения потока по дугам сети могут изменяться в зависимости от времени отправления потока. Будем называть такие задачи «динамическими». Данная область исследования является малоизученной. Учитывая это, а также нечеткий характер параметров, присущий транспортным сетям, приходим к рассмотрению потоковых задач в динамических транспортных сетях в нечетких условиях [8]. В частности, рассмотрим в данной статье задачу определения потока минимальной стоимости в нечеткой динамической транспортной сети.
Задача нахождения максимального потока минимальной стоимости в нечеткой динамической транспортной сети
Рассмотрим постановку задачу нахождения максимального потока минимальной стоимости в нечеткой динамической транспортной сети:
![]()
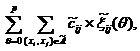 (1)
(1)
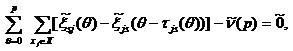 (2)
(2)
![]() (3)
(3)
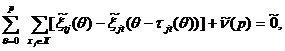 (4)
(4)
![]() (5)
(5)
Выражение (1) означает, что необходимо найти минимальный маршрут перевозки максимального количества потока в транспортной сети за заданное количество моментов времени. Выражение (2) показывает, что максимальное количество потока ![]() за p периодов времени, равно потоку, выходящему из источника за p периодов времени
за p периодов времени, равно потоку, выходящему из источника за p периодов времени ![]() Выражение (4) показывает, что максимальное количество потока
Выражение (4) показывает, что максимальное количество потока ![]() за p периодов времени равно потоку, входящему в сток за p периодов времени
за p периодов времени равно потоку, входящему в сток за p периодов времени ![]() Количество потока
Количество потока ![]() , входящее в источник за p периодов времени, равно количеству потока, покидающему сток
, входящее в источник за p периодов времени, равно количеству потока, покидающему сток ![]() за p периодов времени и равно
за p периодов времени и равно ![]() . В (3) утверждается, что для каждого узла
. В (3) утверждается, что для каждого узла ![]() , кроме источника и стока, и каждого момента времени
, кроме источника и стока, и каждого момента времени ![]() количество потока
количество потока ![]() , вошедшее в
, вошедшее в ![]() в момент времени
в момент времени![]() равно числу единиц потока
равно числу единиц потока ![]() , выходящему из
, выходящему из ![]() в момент
в момент ![]() . Неравенство (5)показывает, что потоки
. Неравенство (5)показывает, что потоки ![]() для всех моментов времени должны быть меньше пропускных способностей
для всех моментов времени должны быть меньше пропускных способностей ![]() по соответствующим дугам.
по соответствующим дугам.
Иными словами, необходимо перевезти ![]() единиц потока с минимальными затратами в динамической транспортной сети, так, чтобы последняя единица потока вошла в сток в момент времени не позднее p.
единиц потока с минимальными затратами в динамической транспортной сети, так, чтобы последняя единица потока вошла в сток в момент времени не позднее p.
Формальный алгоритм решения данной задачи:
Этап 1. Перейти от заданного нечеткого динамического графа ![]() к «растянутому во времени» на p интервалов нечеткому статическому графу
к «растянутому во времени» на p интервалов нечеткому статическому графу ![]() путем «растягивания во времени» исходного динамического графа за заданное количество временных интервалов путем создания отдельной копии каждой вершины
путем «растягивания во времени» исходного динамического графа за заданное количество временных интервалов путем создания отдельной копии каждой вершины ![]() в каждый рассматриваемый момент времени
в каждый рассматриваемый момент времени ![]() . Пусть
. Пусть ![]() представляет собой «растянутый во времени» граф исходного динамического графа. Множество вершин
представляет собой «растянутый во времени» граф исходного динамического графа. Множество вершин ![]() графа
графа ![]() задается как
задается как ![]() Множество дуг
Множество дуг ![]() состоит из дуг, идущих из каждой пары «вершина-время»
состоит из дуг, идущих из каждой пары «вершина-время» ![]() в каждую пару «вершина время» вида
в каждую пару «вершина время» вида ![]() где
где ![]() и
и ![]() . Пропускные способности
. Пропускные способности ![]() , соединяющие пары «вершина-время»
, соединяющие пары «вершина-время» ![]() с
с ![]() равны
равны ![]() , стоимость перевозки
, стоимость перевозки ![]() единицы потока по дуге, соединяющей пару «вершина-время»
единицы потока по дуге, соединяющей пару «вершина-время» ![]() с
с ![]() , равна
, равна ![]() Вводим искусственный источник
Вводим искусственный источник ![]() и сток
и сток ![]() и соединяем
и соединяем ![]() дугами с каждым истинным источником, а
дугами с каждым истинным источником, а ![]() с каждым истинным стоком. Фиктивные дуги, идущие от искусственных вершин, имеют бесконечную пропускную способность и нулевую стоимость. Ищем максимальный поток от
с каждым истинным стоком. Фиктивные дуги, идущие от искусственных вершин, имеют бесконечную пропускную способность и нулевую стоимость. Ищем максимальный поток от ![]() к
к ![]() .
.
Этап 2. Строим нечеткую остаточную сеть ![]() для «растянутого во времени графа»
для «растянутого во времени графа» ![]() в зависимости от величин, идущих по дугам графа потоков. Нечеткая остаточная сеть
в зависимости от величин, идущих по дугам графа потоков. Нечеткая остаточная сеть ![]() строится по «растянутой во времени» сети
строится по «растянутой во времени» сети ![]() в зависимости от величин потоков
в зависимости от величин потоков ![]() , (далее
, (далее ![]() ), идущих по дугам последней следующим образом: каждая дуга в остаточной нечеткой сети
), идущих по дугам последней следующим образом: каждая дуга в остаточной нечеткой сети ![]() , соединяющая пару «вершина-время»
, соединяющая пару «вершина-время» ![]() с парой «вершина-время»
с парой «вершина-время» ![]() , по которой поток
, по которой поток ![]() отправляется в момент времени
отправляется в момент времени ![]() имеет нечеткую остаточную пропускную способность
имеет нечеткую остаточную пропускную способность ![]() , стоимость
, стоимость ![]() с временем прохождения
с временем прохождения ![]() и обратную дугу, соединяющую
и обратную дугу, соединяющую ![]() с
с ![]() с остаточной пропускной способностью
с остаточной пропускной способностью ![]() , стоимостью
, стоимостью ![]() и временем прохождения потока по данной дуге
и временем прохождения потока по данной дуге ![]()
Этап 3. Ищем путь ![]() минимальной стоимости по алгоритму Форда из искусственного источника
минимальной стоимости по алгоритму Форда из искусственного источника ![]() в искусственный сток
в искусственный сток ![]() в построенной нечеткой остаточной сети, начиная с нулевых значений потоков.
в построенной нечеткой остаточной сети, начиная с нулевых значений потоков.
(I) Если путь ![]() найден, переходим к этапу 4.
найден, переходим к этапу 4.
(II) Если пути не удалось найти, то получен максимальный поток ![]() минимальной стоимости
минимальной стоимости ![]() в растянутом во времени статическом нечетком графе из
в растянутом во времени статическом нечетком графе из ![]() в
в ![]() , и переходим к шагу 5.
, и переходим к шагу 5.
Этап 4. Пускаем по найденному пути максимальное количество единиц потока в зависимости от ребра в остаточной сети с минимальной остаточной пропускной способностью ![]() .
.
Этап 5. Обновляем значения потоков в графе ![]() : для дуг, соединяющих пару «вершина-время»
: для дуг, соединяющих пару «вершина-время» ![]() с
с ![]() в
в ![]() с неположительной модифицированной стоимостью
с неположительной модифицированной стоимостью ![]() изменяем поток
изменяем поток ![]() по соответствующим дугам, идущим из
по соответствующим дугам, идущим из ![]() в
в ![]() из
из ![]() с
с ![]() на
на ![]() . Для дуг, соединяющих пару «вершина-время»
. Для дуг, соединяющих пару «вершина-время» ![]() с
с ![]() в
в ![]() с неотрицательной модифицированной стоимостью
с неотрицательной модифицированной стоимостью ![]() изменяем поток
изменяем поток ![]() по дугам, идущим из
по дугам, идущим из ![]() в
в ![]() из
из ![]() с
с ![]() на
на ![]() и переходим к этапу 2, начиная с нового значения потока по дугам и заменяя значение потока в графе
и переходим к этапу 2, начиная с нового значения потока по дугам и заменяя значение потока в графе ![]() :
: ![]() .
.
Этап 6. Если найден максимальный поток ![]() минимальной стоимости
минимальной стоимости ![]() в графе
в графе ![]() из фиктивного источника
из фиктивного источника ![]() в фиктивный сток
в фиктивный сток ![]() , определяемый множеством путей
, определяемый множеством путей ![]() , переходим к первоначальному динамическому графу
, переходим к первоначальному динамическому графу ![]() следующим образом: отбрасываем искусственные вершины
следующим образом: отбрасываем искусственные вершины ![]() ,
, ![]() и дуги, соединяющие их с другими вершинами. Таким образом, в исходном динамическом графе
и дуги, соединяющие их с другими вершинами. Таким образом, в исходном динамическом графе ![]() получен максимальный поток
получен максимальный поток ![]() минимальной стоимости, эквивалентный потоку из источников (начальная вершина исходного графа, растянутая на p интервалов) в стоки (конечная вершина, растянутая на p интервалов) в графе
минимальной стоимости, эквивалентный потоку из источников (начальная вершина исходного графа, растянутая на p интервалов) в стоки (конечная вершина, растянутая на p интервалов) в графе ![]() после удаления фиктивных вершин, а каждый путь, соединяющий вершины
после удаления фиктивных вершин, а каждый путь, соединяющий вершины ![]() и
и ![]() , по которому идет поток
, по которому идет поток ![]() стоимости
стоимости ![]() соответствует потоку
соответствует потоку ![]() . стоимости
. стоимости ![]() .
.
Численный пример, реализующий работу алгоритма
Рассмотрим пример, иллюстрирующий реализацию описанного алгоритма. Пусть транспортная сеть, являющаяся частью железнодорожной карты, представлена в форме нечеткой транспортной сети, полученной из ГИС «Object Land» [9] , как показано на рис.1. Понятие «ГИС» представлено в [10].

Рис. 1. – Исходный динамический граф ![]()
Вершина ![]() представляет собой источник, вершина
представляет собой источник, вершина ![]() – сток. Нечеткие пропускные способности и стоимости, а также параметры времени прохождения потока по дугам, зависящие от момента отправления потока представлены в виде таблиц № 1, 2 и 3. Необходимо найти минимальную стоимость перевозки максимального количества единиц потока
– сток. Нечеткие пропускные способности и стоимости, а также параметры времени прохождения потока по дугам, зависящие от момента отправления потока представлены в виде таблиц № 1, 2 и 3. Необходимо найти минимальную стоимость перевозки максимального количества единиц потока ![]() . Правила оперирования с нечеткими треугольными числами представлены в [6].
. Правила оперирования с нечеткими треугольными числами представлены в [6].
Строим остаточную сеть, как показано на рис.2. Так как остаточная сеть на первом шаге совпадает с исходным «растянутым во времени» графом, находим в ней путь минимальной стоимости от ![]() к
к ![]() по алгоритму Форда в
по алгоритму Форда в ![]() . Получаем путь
. Получаем путь ![]() стоимости
стоимости ![]() условных единиц и передаем по нему
условных единиц и передаем по нему ![]() общей стоимости
общей стоимости ![]() единиц потока, что показано на рис.3.
единиц потока, что показано на рис.3.
Таблица № 1
Нечеткие пропускные способности, зависящие от момента отправления потока
Момент времени |
Нечеткие пропускные способности по дугам графа |
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
Таблица № 2
Нечеткие стоимости, зависящие от момента отправления потока
Момент времени |
Нечеткие стоимости по дугам граф |
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
Переходим к построению «растянутого во времени графа» ![]() , как на рис.2. Строим остаточную сеть исходя из нового значения потока по дугам графа, как показано на рис.4. Находим путь минимальной стоимости в построенной остаточной сети от
, как на рис.2. Строим остаточную сеть исходя из нового значения потока по дугам графа, как показано на рис.4. Находим путь минимальной стоимости в построенной остаточной сети от ![]() к
к ![]() по алгоритму Форда. Получаем путь
по алгоритму Форда. Получаем путь ![]() стоимости
стоимости ![]() условных единиц и передаем по нему
условных единиц и передаем по нему ![]() единиц потока общей стоимости
единиц потока общей стоимости ![]() , тогда поток переходит в (рис.5).
, тогда поток переходит в (рис.5).
Таблица № 3
Параметры времени прохождения потока по дугам
Момент времени |
Время прохождения потока по дугам графа |
|||||
|
|
|
|
|
|
|
|
|
0 |
1 |
4 |
4 |
2 |
5 |
1 |
|
1 |
1 |
3 |
1 |
4 |
4 |
4 |
|
2 |
3 |
1 |
3 |
1 |
3 |
1 |
|
3 |
2 |
1 |
3 |
2 |
3 |
1 |

Рис. 2. – ![]() – «растянутый во времени» вариант графа
– «растянутый во времени» вариант графа ![]()

Рис. 3. – Граф ![]() с потоком
с потоком ![]() единиц
единиц

Рис. 4. – Остаточная сеть ![]() после нахождения потока
после нахождения потока

Рис. 5. – Граф ![]() с новым значением потока
с новым значением потока
Строим остаточную сеть исходя из нового значения потока по дугам графа, как показано на рис.6. Так как в данной сети не существует увеличивающего пути, найден максимальный поток минимальной стоимости.

Рис. 6. – Остаточная сеть ![]() после нахождения потока
после нахождения потока
Отбрасывая искусственные вершины и дуги с потоком, соединяющие их с другими вершинами, получаем максимальный поток ![]() единиц минимальной стоимости
единиц минимальной стоимости ![]() условных единиц. Переходя к динамическому графу
условных единиц. Переходя к динамическому графу ![]() от «растянутого во времени» статического графа
от «растянутого во времени» статического графа ![]() , можно сделать вывод, что максимальный поток
, можно сделать вывод, что максимальный поток ![]() за 3 интервала времени равен потоку, выходящему из пар «вершина-время»
за 3 интервала времени равен потоку, выходящему из пар «вершина-время» ![]() и
и ![]() и входящему в пару «вершина-время»
и входящему в пару «вершина-время» ![]() , т.е.
, т.е. ![]() единиц, которые определяются путем
единиц, которые определяются путем ![]() , который отправляется в момент времени
, который отправляется в момент времени ![]() и прибывает в сток в момент времени
и прибывает в сток в момент времени ![]() и путем
и путем ![]() , который отправляется в момент времени
, который отправляется в момент времени ![]() и прибывает в сток в момент времени
и прибывает в сток в момент времени ![]() .
.
Заключение
Данная статья рассматривает алгоритм нахождения максимального потока минимальной стоимости в нечеткой динамической транспортной сети. Практическая ценность рассматриваемого метода в том, что он позволяет решать задачи нахождения оптимального маршрута перевозки максимального количества потока от начального пункта к конечному. Актуальность рассматриваемого алгоритма в том, что он принимает во внимание нечеткий характер параметров транспортной сети, а также зависимость параметров транспортной сети от времени отправления потока.
Литература:
- Форд, Л.Р. Потоки в сетях [Текст] / Л.Р. Форд, Д.Р. Фалкерсон. – М: Мир, 1966. – 276 с.
- Крисофидес, Н. Теория графов. Алгоритмический подход [Текст] / Н. Кристофидес. – М: Мир, 1978. – 432 с.
- Майника, Э. Алгоритмы оптимизации на сетях и графах [Текст] / Э. Майника – М: Мир, 1981. – 326 с.
- Целигоров, Н.А., Целигорова, Е.Н., Мафура, Г.В. Математические модели неопределенностей систем управления и методы, используемые для их исследования [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4. – Режим доступа: http://ivdon.ru/magazine/archive/ n4p2y2012/1340 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Bozhenyuk, A., Gerasimenko, E., Rozenberg, I. The task of minimum cost flow finding in transportation networks in fuzzy conditions [Text] // Proceedings of the 10th International FLINS Conference on Uncertainty Modeling in Knowledge Engineering and Decision Making Word Scientific, Istanbul, Turkey, 26-29 August 2012. – pp. 354-359
- Bozhenyuk, A., Gerasimenko, E., Rozenberg, I. The methods of maximum Flow and minimum cost flow finding in fuzzy network [Text] // Proceedings of the Concept Discovery in Unstructured Data Workshop (CDUD 2012) co-located with the 10th International Conference on Formal Concept Analysis (ICFCA 2012) May 2012, Katholieke Universiteit Leuven, Leuven, Belgium 2012. – pp. 1-12.
- Боженюк, А.В. Анализ и исследование потоков и живучести в транспортных сетях при нечетких данных [Текст] // А.В. Боженюк, И.Н. Розенберг, Т.А. Старостина – М: Научный мир, 2006. – 136 с.
- Bozhenyuk, A., Gerasimenko, E., Rozenberg, I. Algorithm of maximum dynamic flow finding in a fuzzy transportation network [Text] // Proceedings of East West Fuzzy Colloquium 2012 19th Zittau Fuzzy Colloquium, September 5 – 7, pp. 125-132.
- Rozenberg, I., Gittis, C., Svyatov, D. Geoinformation system Object Land [Text] // Proceedings of IPI RAN Systems and Means of Informatics. – Science, Moscow, 2000.
- Клаус, Н.Г., Клаус, А.И. Практика интеграции геоинформационных систем и многоагентных моделей в исследовании социальных конфликтов [Электронный ресурс] // «Инженерный вестник Дона», 2011, №1. – Режим доступа: http://ivdon.ru/magazine/archive/ n1y2011/400 (доступ свободный) – Загл. с экрана. – Яз. рус.