Универсальный метод синтеза оптимальных управлений нелинейными Лагранжевыми динамическими системами
Аннотация
Дата поступления статьи: 25.09.2013Предлагаемый универсальный метод синтеза оптимальных управлений обеспечивает решение задачи синтеза на классе кусочно-постоянных функций для Лагранжевых динамических систем, причем форма закона управления зависит только от структуры целевого функционала и не зависит от структуры действующих на систему обобщенных сил. Эффективность метода подтверждается минимумом вычислительных затрат, а также максимумом скорости сходимости и точности достижения желаемой траектории в сравнении с известным решением на примере ставшей тестовой для проверки различных методов задачи синтеза управления математическим маятником.
Ключевые слова: объединенный принцип максимума, оптимальное управление, математический маятник
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
Введение
Неизменным практическим интересом характеризуются задачи синтеза оптимальных управлений сложными техническими объектами, например, манипуляционными роботами, ракетой и т.п. [1] Это связано с ситуацией, когда существует большое количество вариантов законов управления для линейных динамических систем, а высокой практической значимостью обладают обычно нелинейные случаи. Для них известные методы, как правило, обеспечивают синтез управлений только при введении различного рода упрощений и ограничений [2]. Поэтому проблема синтеза оптимального управления нелинейной динамической системой остается актуальной. При этом в качестве тестовых управляемых объектов при исследовании новых алгоритмов управления достаточно часто используются маятники.
Существенный вклад на пути решения проблемы синтеза внес А.А. Фельдбаум [3]. Важным этапом в решении проблемы синтеза является теория аналитического конструирования регуляторов, связанная с именами А.М. Летова, Р.Э. Калмана, А.А. Красовского [4, 5, 6]. Это направление развивается в рамках поставленной академиком А.А. Красовским крупной научной проблемы поиска оптимального управления с использованием информации о свойствах исследуемого объекта в виде физических законов сохранения, что и привело к созданию концепции обратных задач динамики [7, 8].
На ее основе Пятницким Е.С. и Крутько П.Д. [7, 8] синтезированы имеющие оригинальную структуру управления. При этом применение предложенного в [8] метода декомпозиции затруднено отсутствием рекомендаций по построению функции, входящей в обратную связь, а полученные в [7] с привлечением функций Ляпунова решения обратных задач динамики при синтезе оптимального управления, как правило, квазиоптимальны или оптимальны для линейных систем.
Идея учета физических особенностей динамической системы также лежит в основе методов синергетического подхода [9]. С ее помощью решаются задачи управления нелинейными объектами, но часто синтезируемые таким образом управления являются структурно-сложными, зависят от эвристических коэффициентов, кроме того не доказана их связь с оптимальными решениями.
Известны конструктивные результаты решения обозначенной проблемы, полученные с использованием вариационных принципов механики [12 - 23]. Поэтому цель настоящего научного исследования – разработка метода синтеза оптимальных управлений нелинейными Лагранжевыми динамическими системами.
Для достижения поставленной цели в работе применяется подход, заключающийся в рассмотрении неизвестных причинных характеристик как обобщенных сил, подлежащих определению на основе аппарата объединенного принципа максимума (ОПМ) [12 - 23]. Он базируется на применении игольчатого варьирования к инвариантным признакам действительного движения в форме интеграла действия Гамильтона – Остроградского [24]. Его эффективность подтверждается результатами решения задачи синтеза управления из области кусочно-постоянных функций для нелинейной динамической системы второго порядка.
Постановка задачи синтеза оптимального управления
Движение управляемой системы подчиняется принципу Гамильтона-Остроградского на конечном промежутке времени ![]() [22]
[22]
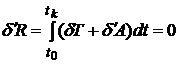 , (1)
, (1)
![]() ;
;
мерой качества управляемого процесса выбран целевой функционал
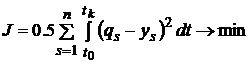 , (2)
, (2)
где ![]() - заданный закон движения,
- заданный закон движения, ![]() - обобщенные координаты и скорости;
- обобщенные координаты и скорости; 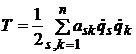 - кинетическая энергия,
- кинетическая энергия, ![]() - коэффициенты инерции;
- коэффициенты инерции; 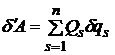 - элементарная работа обобщенных сил, зависящих от управлений,
- элементарная работа обобщенных сил, зависящих от управлений, ![]() ,
, ![]() - число искомых параметров управления. Управления выбираются из замкнутого множества
- число искомых параметров управления. Управления выбираются из замкнутого множества ![]() . В качестве функций управления может назначаться и обобщенная сила
. В качестве функций управления может назначаться и обобщенная сила ![]() .
.
Из принципа (1) следуют уравнения Лагранжа второго рода
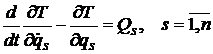 . (3)
. (3)
Задача состоит в построении таких допустимых управлений ![]() или
или ![]() , которые переводят систему (3) из начального состояния
, которые переводят систему (3) из начального состояния ![]() в конечное
в конечное ![]() , а целевой функционал (2) принимает при этом минимальное значение.
, а целевой функционал (2) принимает при этом минимальное значение.
Необходимые и достаточные условия оптимальности управления
Пусть по правилу множителей Лагранжа составлен расширенный функционал
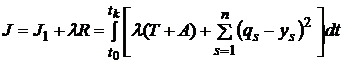 , (4)
, (4)
где ![]() - неопределенный множитель Лагранжа.
- неопределенный множитель Лагранжа.
Теорема. Для того чтобы обобщенная сила ![]() и соответствующая ей траектория
и соответствующая ей траектория ![]() доставляли минимум расширенному функционалу (4), необходимо и достаточно выполнить условия максимума для обобщенной мощности
доставляли минимум расширенному функционалу (4), необходимо и достаточно выполнить условия максимума для обобщенной мощности
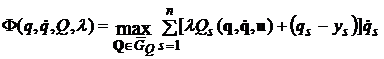 ,(5)
,(5)
при этом ![]() , а на концах траектории
, а на концах траектории ![]() выполняются условия трансверсальности для функции Гамильтона-Остроградского
выполняются условия трансверсальности для функции Гамильтона-Остроградского ![]() и обобщенного кинетического потенциала
и обобщенного кинетического потенциала ![]()
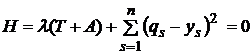 ; (6)
; (6)
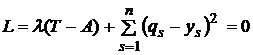 , (7)
, (7)
где ![]() - обобщенные импульсы [24].
- обобщенные импульсы [24].
Доказательство. Асинхронная вариация функционала, обусловленная вариацией обобщенной силы ![]() , будет иметь вид [18]
, будет иметь вид [18]
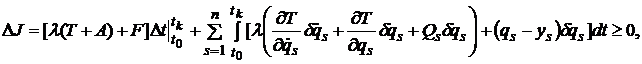 (8)
(8)
где ![]() - синхронные вариации обобщенных координат и скоростей;
- синхронные вариации обобщенных координат и скоростей; ![]() - асинхронная вариация.
- асинхронная вариация.
Интегрирование по частям первого слагаемого под знаком интеграла и замена в граничных условиях синхронной вариации так, чтобы асинхронная вариация равнялась нулю ![]() , откуда
, откуда ![]() , преобразует первое слагаемое под знаком интеграла выражении (8) к виду [18]
, преобразует первое слагаемое под знаком интеграла выражении (8) к виду [18]
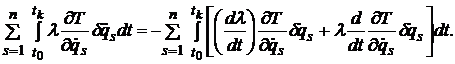 (9)
(9)
Из этого выражения следует, что ![]() , а при преобразовании краевых условий использовано выражение
, а при преобразовании краевых условий использовано выражение ![]() . С учетом преобразований первая асинхронная вариация (8) приводится к условиям трансверсальности (6), (7) и выражению
. С учетом преобразований первая асинхронная вариация (8) приводится к условиям трансверсальности (6), (7) и выражению
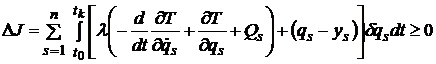 . (10)
. (10)
Из (10) следует (5) [17, 18]. Достаточность выполнения условия максимума для функции обобщенной мощности поясняется следующими преобразованиями.
Пусть из допустимой области ![]() выбрана другая обобщенная сила, полученная из первой игольчатым варьированием
выбрана другая обобщенная сила, полученная из первой игольчатым варьированием ![]() ,
, ![]() при
при ![]() , [6, 22]. Асинхронная вариация функционала для этой обобщенной силы запишется аналогично (10)
, [6, 22]. Асинхронная вариация функционала для этой обобщенной силы запишется аналогично (10)
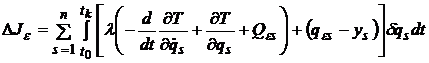 . (11)
. (11)
В силу произвольности синхронные вариации можно положить одинаковыми ![]() при
при ![]() . Из сравнения (10) и (11) получается вторая асинхронно-игольчатая вариация функционала
. Из сравнения (10) и (11) получается вторая асинхронно-игольчатая вариация функционала
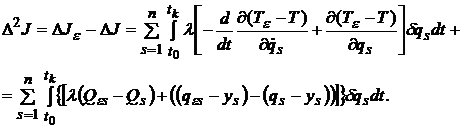 (12)
(12)
Отрезок ![]() можно разделить на три части [6, 17]. На полуоткрытом интервале I
можно разделить на три части [6, 17]. На полуоткрытом интервале I ![]() произвольная и варьированная обобщенные силы совпадают, поэтому
произвольная и варьированная обобщенные силы совпадают, поэтому ![]() . На ограниченном замкнутом интервале
. На ограниченном замкнутом интервале
II ![]()
![]() , но в силу малости интервала
, но в силу малости интервала ![]() ,
,
![]() , [25]. Вторая вариация функционала определяется соотношением
, [25]. Вторая вариация функционала определяется соотношением
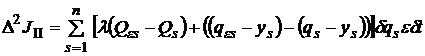 , (13)
, (13)
и соответственно
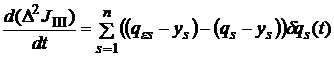 ;
; ![]() (14)
(14)
При предельном переходе ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Из (12) с учетом (2) получается
. Из (12) с учетом (2) получается
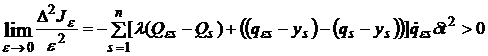 (15)
(15)
Если обобщенная сила ![]() соответствует минимуму целевого функционала, то из (15) вытекает, что условие (5) не нарушается вдоль траектории, так как в соответствии с (14) и предельным переходом величина
соответствует минимуму целевого функционала, то из (15) вытекает, что условие (5) не нарушается вдоль траектории, так как в соответствии с (14) и предельным переходом величина ![]() вдоль траектории
вдоль траектории ![]() .
.
Пример. Решение задачи синтеза оптимальной системы управления нелинейным объектом
Решается задача синтеза оптимальной системы управления нелинейным объектом, уравнения возмущенного движения которого имеют вид [9]:
![]() ,
, ![]() (16)
(16)
Математическая модель (16) описывает движение математического маятника в неустойчивом положении, где ![]() - угол отклонения от вертикали,
- угол отклонения от вертикали, ![]() - момент, приложенный к маятнику [9, 15]. Необходимо отметить, что ее часто используют в качестве тестового объекта управления. Она, например, представляет собой упрощенную модель однозвенного манипуляционного робота с абсолютно жесткими элементами конструкции. Такой манипулятор может совершать движения в плоскости и управляется моментами сил, создаваемыми в идеальных цилиндрических шарнирах. В этом случае
- момент, приложенный к маятнику [9, 15]. Необходимо отметить, что ее часто используют в качестве тестового объекта управления. Она, например, представляет собой упрощенную модель однозвенного манипуляционного робота с абсолютно жесткими элементами конструкции. Такой манипулятор может совершать движения в плоскости и управляется моментами сил, создаваемыми в идеальных цилиндрических шарнирах. В этом случае ![]() - угол поворота динамического звена относительно основания [26]. Уравнение (16) также описывает движение асинхронного электродвигателя с маятником на валу в предположении отсутствия трения. Тогда
- угол поворота динамического звена относительно основания [26]. Уравнение (16) также описывает движение асинхронного электродвигателя с маятником на валу в предположении отсутствия трения. Тогда ![]() - относительная угловая координата положения вала асинхронного электродвигателя [27].
- относительная угловая координата положения вала асинхронного электродвигателя [27].
Требуется синтезировать управление ![]() , обеспечивающее изменение угла
, обеспечивающее изменение угла ![]() в соответствии с желаемой траекторией
в соответствии с желаемой траекторией ![]() :
:
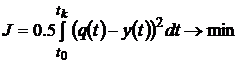 . (17)
. (17)
Пусть желаемая траектория находятся из дифференциального уравнения [9]
![]() ,
, ![]() . (18)
. (18)
Таким образом, цель управления состоит в приведении исследуемой динамической системы по заданной траектории из начального состояния ![]() в точку фазового пространства
в точку фазового пространства ![]() . Соответственно, данная постановка отвечает задаче удержания манипулятора робота в верхнем неустойчивом положении или обеспечения требуемого режима разгона, торможения асинхронного электродвигателя с маятником.
. Соответственно, данная постановка отвечает задаче удержания манипулятора робота в верхнем неустойчивом положении или обеспечения требуемого режима разгона, торможения асинхронного электродвигателя с маятником.
Тогда использование теоремы объединенного принципа максимума для поставленной задачи позволит получить следующий закон управления [23]
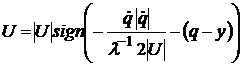 , (19)
, (19)
где ![]() - допустимое управление. Его форма соответствует известному решению принципа максимума Л.С. Понтрягина [11].
- допустимое управление. Его форма соответствует известному решению принципа максимума Л.С. Понтрягина [11].
Анализ эффективности синтезированной обратной связи проведен на основе сравнения с конструктивным вариантом решения поставленной задачи из [9]. Он определяется следующим дифференциальным уравнением:
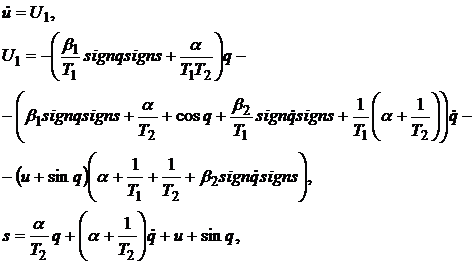 (20)
(20)
где ![]() - параметры настройки, которые находятся из (18).
- параметры настройки, которые находятся из (18).
При этом необходимо отметить, что решение поставленной задачи синтеза (16), (17) на основе ОПМ приводит к получению закона управления, вид которого для Лагранжевой динамической системы не зависит от обобщенных сил правой части (16). Структура управления определяется целевым функционалом (17). Использование принципа максимума Л.С. Понтрягина в задачах синтеза требует поиска и анализа решения краевой задачи с целью определения явной формы обратной связи для каждой конкретной динамической системы, что часто затруднительно. Применение методологии изложенной в [9] также относительно трудоемко. Полученные решения, как правило, отличаются громоздкостью. Кроме того, такая процедура требует вычисления параметров ![]() [9, 15], которые в соответствии с (18) определяют желаемую траекторию
[9, 15], которые в соответствии с (18) определяют желаемую траекторию ![]() .
.
Результаты математического моделирования показаны на рисунке 1. Здесь цифрами обозначено: 1, 3 – соответственно динамика угла отклонения маятника от вертикали ![]() и скорости его изменения при использовании (19); 2, 4 - соответственно динамика угла отклонения маятника от вертикали
и скорости его изменения при использовании (19); 2, 4 - соответственно динамика угла отклонения маятника от вертикали ![]() и скорости его изменения при использовании (20). Видно, что при выбранных параметрах, когда
и скорости его изменения при использовании (20). Видно, что при выбранных параметрах, когда ![]() ,
, ![]() , кривые желаемого движения и управляемого с использованием (19) совпадают с высокой точностью в отличие от (20). Все величины приведены в безразмерных единицах. Следует отметить, что более детальный выбор параметров закона управления (20) позволяет существенно повысить точность расчетов. Анализ переходных процессов позволяет сделать вывод о превосходстве ОПМ над (20) по критерию быстродействия и точности. При этом для (19)
, кривые желаемого движения и управляемого с использованием (19) совпадают с высокой точностью в отличие от (20). Все величины приведены в безразмерных единицах. Следует отметить, что более детальный выбор параметров закона управления (20) позволяет существенно повысить точность расчетов. Анализ переходных процессов позволяет сделать вывод о превосходстве ОПМ над (20) по критерию быстродействия и точности. При этом для (19) ![]() , а для (20)
, а для (20) ![]() .
.
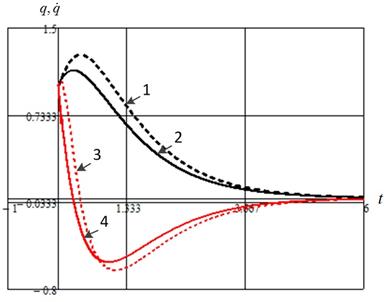
Рис. 1 – Переходные процессы управляемой системы
Структура синтезированных законов изменения моментов, приложенных к маятнику, изображена на рисунке 2, где цифрами обозначено: 1 – закон изменения момента, полученный с использованием (19); 2 – закон изменения момента, полученный с использованием (20).
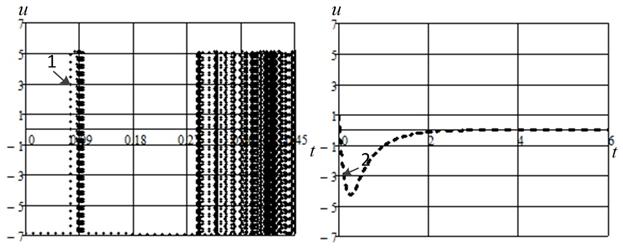
Рис. 2 – Структура синтезированных законов изменения моментов, приложенных к маятнику
Синтезированное управление релейное, что в совокупности с переходным процессом дополнительно подтверждает справедливость выводов о существовании связи между объединенным принципом максимума и принципом максимума Л.С. Понтрягина, которая продемонстрирована совпадением аналитической формы решений в [15, 18] и доказана в [23]. Это следует из того, что для классического решения оптимальные траектории математического маятника должны содержать счетное количество переключений управления, сгущающихся к точке ![]() [28]. В результате в практических задачах часто целесообразно переходить к субоптимальным управлениям или искать решения из области непрерывных функций [11, 14] как, например, (20).
[28]. В результате в практических задачах часто целесообразно переходить к субоптимальным управлениям или искать решения из области непрерывных функций [11, 14] как, например, (20).
Заключение
Анализ полученных результатов позволяет сделать следующие выводы:
- Универсальность метода заключается в том, что он позволяет синтезировать управления, обеспечивающие минимизацию целевого функционала (2), для любых Лагранжевых динамических систем из условия максимума функции обобщенной мощности (5). Его форма остается неизменной независимо от конкретной формы записи выражения (3), которая определяется действующими обобщенными силами и структурой кинетической энергии [17, 19, 24].При этом применение к расширенному функционалу (4) процедуры асинхронно-игольчатого варьирования [24] обеспечивает получение необходимого и достаточного условия минимума, аналогичного по структуре (5), для любого целевого функционала, чье подынтегральное выражение задается определенно положительной функцией обобщенных координат [19].
- Процедура получения условия оптимальности в форме принципа максимума функции обобщенной мощности отличается от ранее известной [15 - 23] детальным исследованием условий трансверсальности, которые получены в форме равенства нулю функции Гамильтона и кинетического потенциала.
- Синтезированное управление (19) отличается от (20) компактностью записи, меньшим в 4.4 раза числом элементарных операций сложения, вычитания, деления и умножения, что определяет его вычислительную эффективность [29], а сама процедура получения обратной связи не предполагает никаких дополнительных предположений, в частности относительно заданного уравнением (18) закона движения. Кроме того, в сравнении с принципом максимума Л.С. Понтрягина не требуется решения двухточечной краевой задачи, которое часто обеспечивает получение лишь программ оптимального управления [25].
- Анализ переходных процессов управляемой динамической системы позволяет сделать вывод о превосходстве над (20) [9] ОПМ по критерию быстродействия и точности, что также подтверждается расчетными значениями целевого функционала (17) для (19) и (20).
- Исследование синтезированного кусочно-постоянного управления позволило установить соответствие законов управления принципа максимума Л.С. Понтрягина и ОПМ.
Таким образом, поставленная цель исследований достигнута.
Литература:
- Браганец С.А., Гольцов А.С., Савчиц А.В. Система адаптивного управления и диагностики сервомоторов направляющего аппарата гидроагрегата с поворотно-лопастной турбиной [Электронный ресурс] // Инженерный вестник Дона. 2013. № 3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2013/1807 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Черноусько Ф.Л., Ананьевский И.М., Решмин С.А. Методы управления нелинейными механическими системами [Текст]: Монография / Черноусько Ф.Л., Ананьевский И.М., Решмин С.А.. – Москва: Физматлит, 2006. – 328 с.
- Фельдбаум А.А. О синтезе оптимальных систем с помощью фазового пространства [Текст] // Автоматика и телемеханика, 1965. - № 2. - С.129 – 149.
- Гурман В.И. Модели и методы теории управления [Текст] // Программные системы: теория и приложения. ИПС РАН. 2004. – №1. –
С. 101 – 116. - Мелса Дж. Л., Сейдж Э.П. Идентификация систем управления. [Текст] М.: Наука, 1974. – 248 с.
- Справочник по теории автоматического управления. [Текст] Под ред. А.А. Красовского. М.: Наука. 1987. - 712 с.
- Крутько П.Д. Обратные задачи динамики в теории автоматического управления. [Текст]: Цикл лекций: Учеб. пособие для ВУЗов / Крутько П.Д. – М.: Машиностроение, 2004. 576 с.
- Пятницкий Е.С. Принцип декомпозиции в управлении механическими системами [Текст] // Доклады академии наук СССР, 1988. Том 300, №2. С. 300 – 303.
- Колесников А.А. Синергетическая теория управления. [Текст] М.: Энергоатомиздат, 1994. 343 с.
- Матюхин В.И. Управление колесной системой в условиях неопределенности [Текст] // Автоматика и телемеханика. – 2009. – № 5. –
С. 76 – 94. - Майкова О.Е. Субоптимальные режимы в задаче Фуллера [Текст] // Труды математического института им. В.А. Стеклова . – 2002. – т. № 236. – С. 226 – 229.
- Kostoglotov A.A., Kostoglotov A.I., Lazarenko S.V. Joint maximum principle in the problem of synthesizing an optimal control of nonlinear systems [Text] // Automatic control and computer sciences – 2007. - V. 41. № 5. – P. 274-281.
- Kostoglotov A.A., Lazarenko S.V. Nonsmooth analysis in measurement processing [Text] // Measurement techniques – 2009. - V. 52. № 2. – P. 117-124.
- Костоглотов А.А. Решение задачи А. Фуллера на основе объединенного принципа Понтрягина – Гамильтона - Остроградского. [Текст] // Автоматика и вычислительная техника. – 2007. – №4. – C. 3 – 14.
- Андрашитов Д.С., Дерябкин И.В., Костоглотов А.А., Кузнецов А.А., Лазаренко С.В. Синтез алгоритма автономного управления математическим маятником на основе объединенного принципа максимума [Текст] // Известия высших учебных заведений. Северо – Кавказский регион. Технические науки. – 2010. – №3. – С. 9 – 14.
- Андрашитов Д.С., Костоглотов А.А., Костоглотов А.И.,
Лазаренко С.В. Многопараметрическая идентификация конструктивных параметров методом объединенного принципа максимума [Электронный ресурс] // Инженерный вестник Дона. 2011. №1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2011/348 (доступ свободный) – Загл. с экрана. – Яз. рус. - Костоглотов А.А., Костоглотов А.И., Лазаренко С.В. Объединенный принцип максимума в задаче синтеза оптимального управления нелинейными системами [Текст] // Автоматика и вычислительная техника. – 2007. – №5. – C. 52 – 61.
- Костоглотов А.А., Костоглотов А.И., Лазаренко С.В. Синтез оптимальных по быстродействию систем на основе объединенного принципа максимума [Текст] // Информационно-измерительные и управляющие системы. – 2007. – №12. – С. 34 – 40.
- Костоглотов А.А., Костоглотов А.И., Лазаренко С.В. Объединенный принцип максимума в задачах оценки параметров движения маневрирующего летательного аппарата [Текст] // Радиотехника и электроника. – 2009. – т.54., №4. – C. 450 – 457.
- Костоглотов А.А., Лазаренко С.В. Метод решения обратных измерительных задач с применением аппарата негладкого анализа [Текст] // Информационно-измерительные и управляющие системы. – 2009. – Т. 7. № 10. – С. 38 – 45.
- Костоглотов А.А., Лазаренко С.В. Негладкий анализ в задачах обработки измерительной информации [Текст] // Измерительная техника. – 2009. – № 2. – С. 6 – 11.
- Костоглотов А.А., Костоглотов А.И., Лазаренко С.В., Ценных Б.М. Метод оценки параметров движения управляемого летательного аппарата на основе объединенного принципа максимума с построением опорной траектории [Текст] // Успехи современной радиоэлектроники. – 2012. – №6. – С. 61 – 66.
- Костоглотов А.А., Костоглотов А.И., Лазаренко С.В., Шевцова Л.А. Синтез оптимального управления на основе объединенного принципа максимума [Текст] // Известия высших учебных заведений. Северо – Кавказский регион. Технические науки. – 2010. – №2. – С. 31 – 37.
- Маркеев А.П. Теоретическая механика. [Текст] М.: Наука, 1990. 416 с.
- Понтрягин Л.С. Математическая теория оптимальных процессов. [Текст] М.: Наука, 1976. 392 с.
- Костоглотов А.А., Костоглотов А.И., Лазаренко С.В., Чеботарев А.В. Метод механико-математического синтеза при построении оптимального управления механическими системами [Текст] // Современные проблемы науки и образования. – 2012. – №6. – http://www.science-education.ru/106-7733
- Луковников В.И., Веппер Л.В. Исследование автоколебательного движения асинхронного электродвигателя с маятником на валу [Текст] // Вестник ГГТУ им. П.О. Сухого. – 2003. – №1. – С. 53 – 60.
- Борисов Б.Ф., Зеликин М.И., Манита Л.А. Экстремали с накоплением переключений [Текст] // Современная математика и ее приложения. Оптимальное управление. – 2008. – Т. 58. – С. 3. – 56.
- Тесты [Текст] // Мобильные компьютеры. 2004. №6. С. 20-39.