Моделирование энергетического спектра в полупроводниковых наноструктурах
Аннотация
Проведен теоретический анализ физической модели полупроводниковой наноструктуры, сформулирована математическая модель, выбран алгоритм решения системы уравнений, приведен пример решения. Ключевые слова: физическая модель, компьютерное моделирование, полупроводник, наноструктура, алгоритм решения, численные расчеты
Таганрогский научно–исследовательский институт связи
Полупроводниковые наноструктуры, создаваемые в настоящее время, благодаря успехам нанотехнологий, вызывают большой интерес из-за новых явлений, проявляющихся при переходе к наноразмерам. Когда размеры структур становятся сравнимы с длиной волны носителей заряда в полупроводниках, появляется возможность управления энергетическим спектром с помощью изменения размера рабочих областей.
Теоретический анализ наноструктур затруднен тем, что точно могут быть решены только некоторые простые задачи. Поэтому распространенным методом теоретического анализа наноструктур является метод компьютерного моделирования. Компьютерное моделирование включает в себя несколько важных этапов:
– постановка задачи. На этом этапе производится теоретический анализ физической модели, устанавливаются ограничения на допустимые пределы изменения параметров, формулируются основные уравнения, граничные (начальные) условия и пределы применимости модели;
– формулировка математической модели. В физической модели выделяются характерные единицы измерения физических величин и, затем, уравнения модели записываются в безразмерном виде. Это необходимо, чтобы исключить в дальнейших расчетах ошибки вычислений, связанные с очень большими или очень маленькими размерными константами, такими как постоянная Планка или масса покоя электрона;
– выбор алгоритма и разработка программы вычислений. Алгоритм вычислений должен обеспечивать необходимую скорость вычислений и заданные погрешности конечных результатов. Программа, реализующая выбранный алгоритм, должна позволять изменять параметры модели и выдавать результаты в удобном и наглядном виде.
– решение и анализ решения. Отладку программы удобно провести на модели, имеющей точное решение, так, чтобы можно было проверить правильность моделирования. Отлаженная таким образом программа, может быть затем применена к задачам, не имеющим точного решения.
Постановка задачи
Для одномерной потенциальной ямы с бесконечно высокими барьерами уравнение Шредингера имеет вид:
![]()
![]() (1)
(1)
Здесь m – эффективная масса носителя заряда. Из-за невозможности проникновения частицы через бесконечно высокий барьер, волновые функции на границах должны обращаться в ноль. Решением уравнения (1) для ямы с плоским дном (U(x)=0) являются волновые функции и энергетические состояния, которые даются формулами [1]:
![]() (2)
(2)![]() (3)
(3)
Максимальная высота барьера в полупроводниках ограничивается работой выхода ![]() эВ.
эВ.
Поэтому,![]() для существования связанных состояний в яме необходимо, чтобы
для существования связанных состояний в яме необходимо, чтобы ![]() <<
<<![]() , то есть
, то есть ![]() . Если
. Если ![]() , то
, то ![]() нм.
нм.
Электрическая подвижность носителей заряда в полупроводниках ![]() , где τ - время релаксации импульса. Неопределенность энергии за время τ будет:
, где τ - время релаксации импульса. Неопределенность энергии за время τ будет: ![]() . Для того, чтобы энергетические состояния в яме были разделены, необходимо чтобы:
. Для того, чтобы энергетические состояния в яме были разделены, необходимо чтобы: ![]() или a << l, где l - длина свободного пробега. В полупроводниках при
или a << l, где l - длина свободного пробега. В полупроводниках при ![]() и
и ![]() см2/в сек размер ямы должен быть
см2/в сек размер ямы должен быть ![]() нм [2].
нм [2].
Математическая модель
Естественным масштабом расстояния в задаче является размер ямы ![]() , который можно принять за единицу измерения длины. Тогда единицей измерения энергии будет величина
, который можно принять за единицу измерения длины. Тогда единицей измерения энергии будет величина ![]() . В безразмерном виде уравнение Шредингера и граничные условия примут вид:
. В безразмерном виде уравнение Шредингера и граничные условия примут вид:
![]() (4)
(4)![]() (5)
(5)
Для ямы с плоским дном (V(x)=0), обозначая ![]() , из (4) получаем:
, из (4) получаем:
![]() (6)
(6)
Решением (6) является собственная функция и собственные значения:
![]() (7)
(7)![]() ;
; ![]() (8)
(8)
Если значения k1вычисляются с погрешностью ![]() , то погрешность волновой функции при x=1 будет
, то погрешность волновой функции при x=1 будет ![]()
Погрешность в энергии:
![]() (9)
(9)
Соотношение (9) показывает допустимую погрешность вычисления граничного значения волновой функции ![]() для достижения заданной погрешности вычисления энергии
для достижения заданной погрешности вычисления энергии ![]() .
.
Алгоритм решения задачи моделирования энергетического спектра
Одним из методов решения граничной задачи (4), (5) является метод пристрелки. В этом методе граничную задачу заменяют задачей Коши с начальными условиями, которыми являются значения функции и производной на одной границе. Другое граничное условие является условием пристрелки, достижение которого является критерием правильности решения. Параметром пристрелки является значение энергии ![]() . Однако, если с начальным условием для функции все ясно:
. Однако, если с начальным условием для функции все ясно: ![]() =0, то как выбрать начальное значение
=0, то как выбрать начальное значение ![]() ? Обращаясь к уравнению (4), видим, что это уравнение является линейным по
? Обращаясь к уравнению (4), видим, что это уравнение является линейным по ![]() . То есть, если
. То есть, если ![]() - решение, то
- решение, то ![]() - тоже решение, где
- тоже решение, где ![]() - любое число. Выбирая произвольные значения
- любое число. Выбирая произвольные значения ![]() , мы, тем самым, умножаем
, мы, тем самым, умножаем ![]() на некоторое (неизвестное нам) число. Но, т.к.
на некоторое (неизвестное нам) число. Но, т.к. ![]() =0, то это начальное значение остается неизменным. Это особенность задачи с нулевым начальным условием. Если бы
=0, то это начальное значение остается неизменным. Это особенность задачи с нулевым начальным условием. Если бы ![]()
![]() 0, то это начальное значение также умножалось бы на произвольное число, и, таким образом, граничное условие было бы нарушено. Если
0, то это начальное значение также умножалось бы на произвольное число, и, таким образом, граничное условие было бы нарушено. Если ![]() - любое, то, помня о теоретических функциях (7), которые имеют порядок единицы, можно просто принять
- любое, то, помня о теоретических функциях (7), которые имеют порядок единицы, можно просто принять ![]() =1. При разработки программ на языках высокого уровня (DELPHI, C++) для численного интегрирования уравнения (4) можно применить метод Рунге-Кутта. Адаптивная программа РКФ-45 [3] реализует метод 4
=1. При разработки программ на языках высокого уровня (DELPHI, C++) для численного интегрирования уравнения (4) можно применить метод Рунге-Кутта. Адаптивная программа РКФ-45 [3] реализует метод 4![]() 5 порядка, где интегрирование происходит методом 4 порядка, а приближение 5 порядка применяется для контроля точности решения на каждом шаге и выбора оптимального шага интегрирования. Применение адаптивной процедуры обеспечивает достижение заданной точности решения на конце интервала интегрирования, то есть второго граничного условия. При применении пакета MATHEMATICA решение уравнения (4) осуществляется функцией NDSolve [4], в параметрах которой необходимо задать нужную точность вычисления и вывода результатов.
5 порядка, где интегрирование происходит методом 4 порядка, а приближение 5 порядка применяется для контроля точности решения на каждом шаге и выбора оптимального шага интегрирования. Применение адаптивной процедуры обеспечивает достижение заданной точности решения на конце интервала интегрирования, то есть второго граничного условия. При применении пакета MATHEMATICA решение уравнения (4) осуществляется функцией NDSolve [4], в параметрах которой необходимо задать нужную точность вычисления и вывода результатов.
Решение задачи моделирования энергетического спектра
Входными параметрами задачи являются: интервал энергий, в котором производится поиск уровня энергии, и погрешность вычисления уровня энергии ![]() . Результатом работы программы являются собственные значения энергии, вычисленные с заданной точностью, и соответствующие им волновые функции. На первом этапе решения производится сканирование всего интервала энергии с большим шагом (однако меньшим, чем расстояние между уровнями) с целью определения интервалов, содержащих искомые уровни энергии. Затем в каждом найденном интервале (например, методом дихотомии) производится поиск значения энергии с заданной погрешностью. При этом в качестве критерия можно использовать соотношение (9) для контроля точности волновой функции на конце интервала интегрирования.
. Результатом работы программы являются собственные значения энергии, вычисленные с заданной точностью, и соответствующие им волновые функции. На первом этапе решения производится сканирование всего интервала энергии с большим шагом (однако меньшим, чем расстояние между уровнями) с целью определения интервалов, содержащих искомые уровни энергии. Затем в каждом найденном интервале (например, методом дихотомии) производится поиск значения энергии с заданной погрешностью. При этом в качестве критерия можно использовать соотношение (9) для контроля точности волновой функции на конце интервала интегрирования.
Если наноструктура образована слоями полупроводников с разной шириной запрещенной зоны, то квантовая яма не может считаться бесконечно глубокой, т.к. высоты барьеров по порядку величины сравнимы с уровнями энергии в яме. Однако, если яма расположена у поверхности, то с одной стороны она ограничена работой выхода и барьер можно считать по-прежнему бесконечно большим. В этом случае задачу также можно решить методом пристрелки. Пусть при x > 1 высота барьера есть V0, тогда правильные волновые функции вне ямы, соответствующие собственным значениям энергии ![]() , будут иметь вид:
, будут иметь вид:
![]()
На длине ![]() волновая функция спадает в е раз. Если на границе ямы при x = 1 волновая функция имеет порядок единицы, то заданной малой величины
волновая функция спадает в е раз. Если на границе ямы при x = 1 волновая функция имеет порядок единицы, то заданной малой величины ![]() функция достигает на длине
функция достигает на длине ![]() . Таким образом, полный интервал интегрирования будет теперь зависеть от значения энергии. Если выбранное значение энергии не соответствует собственному значению, то в численном решении появляется нарастающая экспонента, и решение расходится. Возможен и другой критерий правильности волновой функции при x > 1. Например, можно показать, что
. Таким образом, полный интервал интегрирования будет теперь зависеть от значения энергии. Если выбранное значение энергии не соответствует собственному значению, то в численном решении появляется нарастающая экспонента, и решение расходится. Возможен и другой критерий правильности волновой функции при x > 1. Например, можно показать, что ![]() становится линейной функцией при x>1.
становится линейной функцией при x>1.
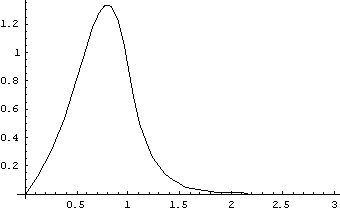
Волновая функция основного состояния при значении энергии основного состояния![]() .
.
Список использованной литературы
1. Л. Д. Ландау, Е. М. Лифшиц Квантовая механика. М., «Наука», 1974.
2. В. Я. Демиховский, Г. А. Вугальтер Физика квантовых низкоразмерных структур. М., «Логос», 2000.
3. Д. Каханер, К. Моулер, С. Нэш Численные методы и программное обеспечение. М., «Мир», 2001.
20 июня 2008 г.