Расчет на устойчивость полимерных стержней с учетом деформаций ползучести и начальных несовершенств
Аннотация
Статья посвящена исследованию потери устойчивости полимерных стержней при наличии возмущающих факторов в виде погиба стержня и наличии эксцентриситета приложения нагрузки.
Ключевые слова: устойчивость стержней, ползучесть, высокоэластические деформации, полимерные материалы, уравнение связи Максвелла-Гуревича.
В настоящее время полимерные материалы используются не только как ограждающие и имеющие «вторичное» значение конструкции, но и как несущие элементы. Примером могут быть полимерные стержни для крепления навесных конструкций. Эти стержни претерпевают как растяжение, так и сжатие.
Основное преимущество полимерных стержней в том, что они являются кислото- и щелочестойкими материалами, прочность некоторых полимеров может достигать 2000 МПа. Однако полимерные материалы обладают свойством ползучести. Для описания деформаций ползучести далее используется уравнение связи Максвелла-Гуревича, которое максимально точно описывает связь напряжений и деформаций ползучести не только в полимерных материалах, но и в некоторых металлах.Уравнение Максвелла-Гуревича далее используется в следующем виде:
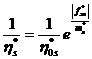
Здесь
![]() – модуль скорости,
– модуль скорости, ![]() – коэффициент начальной релаксационной вязкости.
– коэффициент начальной релаксационной вязкости.
Для полимерных материалов деформации ползучести представлены рядом спектров времен релаксаций![]() ,
, ![]()
При времени деформаций до 1000 часов преобладает первый, старший спектр времен релаксаций, т.е. s=1.
Как видно из выше представленных уравнений определяемые высокоэластические деформации находятся и в левой части уравнения (под оператором дифференцирования), и в правой части (в функции напряжений)![]() . Всвязи с этим при использовании уравнения связи Максвелла-Гуревича возникают трудности в применении таких программных комплексов, как ANSYS. Дальнейшее решение задач происходило в программном комплексе MatLab.
. Всвязи с этим при использовании уравнения связи Максвелла-Гуревича возникают трудности в применении таких программных комплексов, как ANSYS. Дальнейшее решение задач происходило в программном комплексе MatLab.
В практике стержни имеют некоторое искривление своей оси, также называемое «погибью», при этом сила обычно оказывается приложенной внецентренно (см. рис.1.). Подобного рода задачи в упругой постановке подробно рассмотрены в [1, 3].
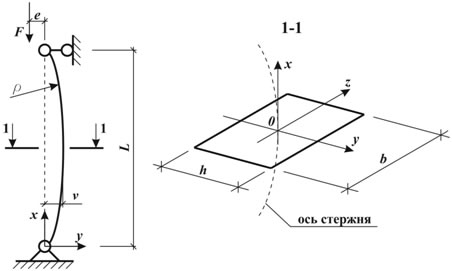
Рис.1. Расчетная схема задачи
Одновременное влияние начальных возмущений и ползучести стержня рассматривалось в работах [1, 4].
При выводе основных уравнений использовались следующие допущения и гипотезы:
1. Имеет место одноосное напряженное состояние (![]() ).
).
2. Гипотеза плоских сечений.
3.Геометрическая линейность (![]() ).
).
4. Форма сечения (рассматривается прямоугольное сечение).
Полную деформацию по оси стержня можно записать в виде
С учетом гипотезы плоских сечений, с другой стороны, можно записать
где ![]() – деформации средней оси стержня;
– деформации средней оси стержня; ![]() – кривизна стержня;
– кривизна стержня;![]() – радиус кривизны.
– радиус кривизны.
С учетом (2) и (3) можно записать
Для любого сечения стержня могут быть записаны интегральные условия
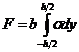 ,
, 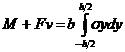 ,(6)
,(6)
где![]() .
.
Подставляя выражение (4) в (5) и проведя интегрирование,определяются осевые деформации стержня:
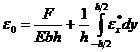 .
. Подставляя выражение (4) в (6) и проведя интегрирование:
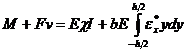 ,
, где![]() - осевой момент инерции сечения стержня относительно оси z.
- осевой момент инерции сечения стержня относительно оси z.
С учетом того, что ![]() получаем окончательное разрешающее уравнение для оси стержня:
получаем окончательное разрешающее уравнение для оси стержня:
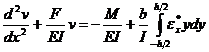 .
. В работах [1, 4] разрешающее уравнение было сведено к двум интегро-дифференциальным уравнениям для двух неизвестных f* и v.
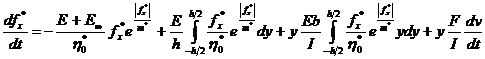 ,
, 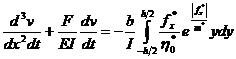 .(11)
.(11)
Однако в таком виде уравнения (10) и (11) могут быть использованы только при применении уравнения связи Максвелла-Гуревича. Уравнение (9) такого недостатка лишено и может использоваться при любом уравнении связи.
Решение уравнения (9) было получено методом конечных разностей, интегралы определялись с помощью метода Симпсона.
Далее рассматриваются задачи ползучести стержня из эпоксидной смолы ЭДТ-10 и полиметилметакрилата (ПММА). При этом исходные данные взяты из работ [1, 4], т.к. в них проводится эксперимент на основе стержня из эпоксидной смолы ЭДТ-10, что позволяет сравнить результаты эксперимента с численным решением задачи. Результат для ПММА получен впервые.
Исходные данные:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]()
Данные для параметров ползучести взяты из работы [2].
ЭДТ-10 |
ПММА |
|
|
|
Результаты расчетов представлены на рисунках 2÷5. Положительным напряжениям соответствует сжатие.
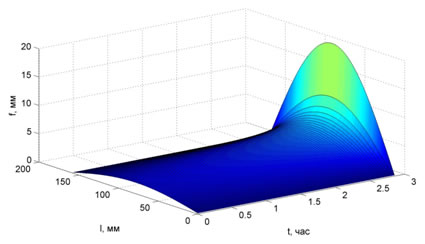
Рис.2. Рост стрелы прогиба во времени в стержне из ЭДТ-10
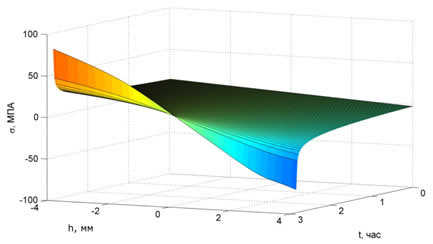
Рис.3. Рост напряжений в сечении стержня из ЭДТ-10 при x=l/2
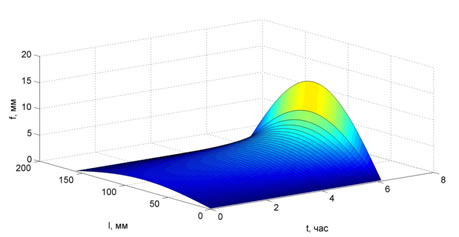
Рис.4. Рост стрелы прогиба во времени в стержне из ПММА
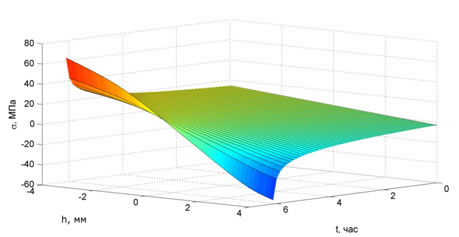
Рис.5. Рост напряжений в сечении стержня из ПММА при x=l/2
Результаты расчета для стержня из ЭДТ-10 полностью совпали с экспериментальными данными. Резкий рост деформаций и напряжений наблюдается при t=2ч 40мин.Таким образом можно говорить и о возможной потери устойчивости образца из ПММА, которая по расчетам должна произойти при t=6ч 05мин.
Литература:
1. Андреев В.И. Устойчивость полимерных стержней при ползучести: дис. … канд. техн. наук. – М., 1967.
2. Бабич В.Ф. Исследование влияния температуры на механические характеристики полимеров: дис. … канд. техн. наук. – М., 1966.
3. Вольмир А.С. Устойчивость деформируемых систем. – М.: Наука, 1975.
4. Языев С.Б. Устойчивость стержней при ползучести с учетом начальных несовершенств: дис. … канд. техн. наук. – Ростов-н/Д, 2010.