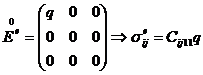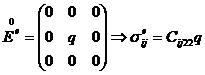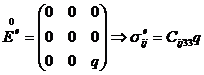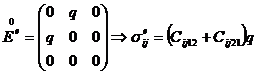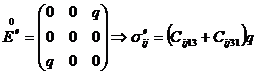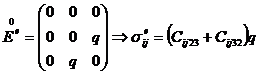Метод и результаты численной оценки эффективных механических свойств резинокордных композитов для случая двухслойного материала
Аннотация
Дата поступления статьи: 22.05.2013Описывается методика и алгоритм численной оценки эффективных механических характеристик резинокордных композитов. Эффективные свойства находятся в виде закона Гука для анизотропных материалов. Выполнены расчёты эффективных характеристик двуслойного резинокорда с помощью CAE "Фидесис". Исследована зависимость эффективных свойств от угла закроя нитей корда.
Ключевые слова: теория упругости, эффективные свойства, прочностные расчёты, резинокорд, численное моделирование, метод конечных элементов, CAE "Фидесис"
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Введение
Резинокордный композит представляет собой обрезиненные [3] нити корда. Этот материал используется, в частности, при изготовлении брекера и каркаса автомобильных пневматических шин [1, 2]. В брекере шин, а также в каркасе диагональных шин применяется многослойный резинокорд, в котором направление нитей корда в двух соседних слоях разное (чередуется от слоя к слою).
При численном прочностном моделировании изделий из резинокорда (как и изделий из других композитных [5, 9, 11] материалов) может использоваться два подхода:
- отдельно учитывается при создании геометрической и механической модели изделия каждая нить корда;
- композитный материал заменяется однородным (так называемым эффективным) материалом, механические свойства которого вычисляются путём осреднения свойств композита и называются эффективными (осреднёнными) свойствами [14].
Для резинокордных деталей первый подход может применяться в областях шины, где достигаются максимальные напряжения в резине между нитями корда (как правило, это область контакта шины с поверхностью): эти максимальные напряжения важно вычислить с высокой точностью, т.к. они влияют на ресурс шины. В остальной части шины вполне может применяться второй подход – замена резинокорда эффективным материалом.
Шины и другие изделия из резинокорда могут испытывать в процессе эксплуатации достаточно большие деформации, поэтому важно учесть при моделировании эффекты геометрической и физической нелинейности. Учет геометрической нелинейности связан с определенными сложностями в определении эффективного материала. Представленный в статье алгоритм основан на подходе, предложенном в [7, 8, 15, 16] и позволяющем преодолеть эти затруднения.
Алгоритм численной оценки эффективных свойств резинокорда
Определим эффективный (осреднённый) материал как однородный материал, удовлетворяющий условию: если этим однородным материалом заполнить представительный объём и исходным резинокордным композитом заполнить такой же представительный объём – то средние напряжения по объёму в исходном и эффективном материале будут равны при одинаковых перемещениях граней. Соответственно, эффективные свойства резинокорда – свойства этого эффективного материала [7, 8, 15, 16].
Исходя из этих определений, эффективные определяющие соотношения резинокордного материала будут строиться следующим образом. Для представительного объёма V0, выделенного в начальном состоянии (т.е. до деформации), решим определённое количество краевых задач теории упругости [6, 10, 12]:
![]() (1)
(1)
с граничными условиями
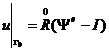 (2)
(2)
где ![]() – оператор градиента в координатах начального состояния,
– оператор градиента в координатах начального состояния,
![]() – тензор истинных напряжений,
– тензор истинных напряжений,
![]() – первый тензор напряжений Пиолы,
– первый тензор напряжений Пиолы,
![]() – радиус-вектор частицы в начальном и текущем состояниях,
– радиус-вектор частицы в начальном и текущем состояниях,
![]() – вектор перемещений,
– вектор перемещений,
![]() – аффинор деформаций,
– аффинор деформаций,
I – единичный тензор.
Механические свойства корда при расчётах описывались законом Гука с константами λ = 110000 МПа, G = 80600 МПа. Свойства резины – определяющими соотношениями Муни-Ривлина [4, 10] с константами C1 = -0.05709 МПа, C2 = 1,05046 МПа.
Каждый тип решаемой задачи соответствует определённому виду тензора деформаций ![]() и определённому виду аффинора деформаций
и определённому виду аффинора деформаций ![]() . Мы будем решать следующие типы задач:
. Мы будем решать следующие типы задач:
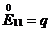 – растяжение или сжатие по оси X,
– растяжение или сжатие по оси X,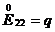 – растяжение или сжатие по оси Y,
– растяжение или сжатие по оси Y,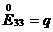 – растяжение или сжатие по оси Z,
– растяжение или сжатие по оси Z,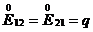 – сдвиг в плоскости XY,
– сдвиг в плоскости XY,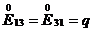 – сдвиг в плоскости XZ,
– сдвиг в плоскости XZ,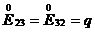 – сдвиг в плоскости YZ,
– сдвиг в плоскости YZ,
где q – величина деформации (в расчётах составляла 0,2%).
Для каждого типа задачи, зная тензор деформаций, найдём аффинор из соотношения
![]() (3)
(3)
Поскольку аффинор деформаций – несимметричный тензор, а тензор деформаций – симметричный, однозначно определить аффинор из тензора деформаций не получится. Поэтому в расчётах аффинор задавался верхнетреугольным – в этом случае шесть его компонент однозначно определялись по шести независимым компонентам тензора деформаций.
Вычислив аффинор деформаций, приложим к представительному объёму граничные условия (2), решим краевую задачу теории упругости (1) и найдём поле тензора напряжений ![]() . Далее найдём эффективный тензор напряжений
. Далее найдём эффективный тензор напряжений ![]() с помощью осреднения по формуле
с помощью осреднения по формуле
![]() (4)
(4)
В формуле (4) используется формула Гаусса-Остроградского и то, что
![]() ,
,
где * – знак транспонирования.
Считая деформации малыми, эффективные определяющие соотношения мы будем искать в виде зависимости полученного осреднённого тензора напряжений от заданного тензора деформаций:
![]() (5)
(5)
Коэффициенты Cijkl вычисляем, зная компоненты осреднённого тензора напряжений для каждой из шести задач:
Поскольку мы ищем эффективные определяющие соотношения в виде (5), вышеуказанных шести последовательностей задач достаточно для вычисления коэффициентов Cijkl. Из симметричности тензора деформаций следует Cijkl = Cijlk. Из симметричности тензора напряжений следует Cijkl = Cjikl. Также выполняется равенство Cijkl = Cklij.
Результаты расчётов
Исследовалась зависимость эффективных характеристик двуслойного резинокорда от угла закроя нитей корда. Свойства корда описывались законом Гука с константами λ = 110000 МПа, G = 80600 МПа. Свойства резины – определяющими соотношениями Муни-Ривлина с константами C1 = -0.05709 МПа, C2 = 1.05046 МПа. Толщина одного слоя резинокорда – 2 мм, диаметр нити – 0,75 мм, частота нитей – 100 штук на 10 см. Расположение нитей в слоях показано на рис. 1.
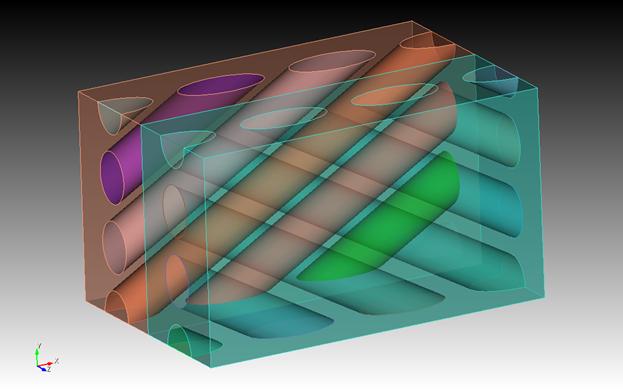
Рис. 1 . Внутренняя структура двуслойного резинокорда.
Численные расчеты напряженно-деформированного состояния в представительном объеме резинокорда осуществлялись методом конечных элементов [17, 18] с использованием системы инженерного прочностного анализа (CAE-системы) ФИДЕСИС [19].
Ниже приведены графики зависимости некоторых коэффициентов Cijkl от угла наклона нитей корда в слоях по отношению к оси абсцисс. Угол варьировался в пределах от 10 до 80 градусов.
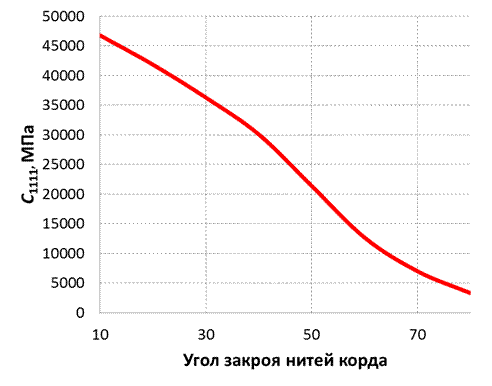
Рис. 2. Зависимость коэффициента C1111 от угла закроя нитей корда.
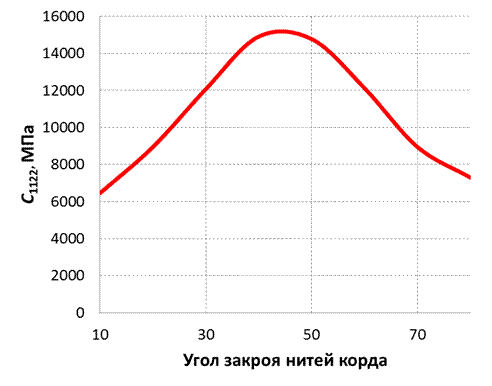
Рис. 3. Зависимость коэффициента C1122 от угла закроя нитей корда.
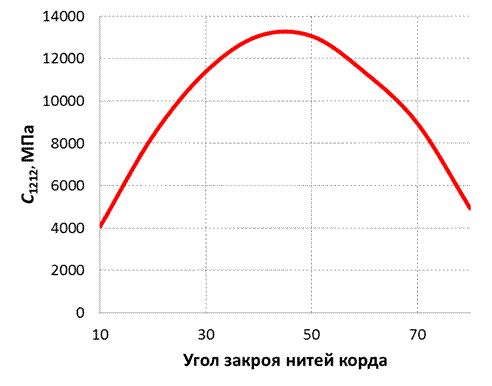
Рис. 4. Зависимость коэффициента C1212 от угла закроя нитей корда.
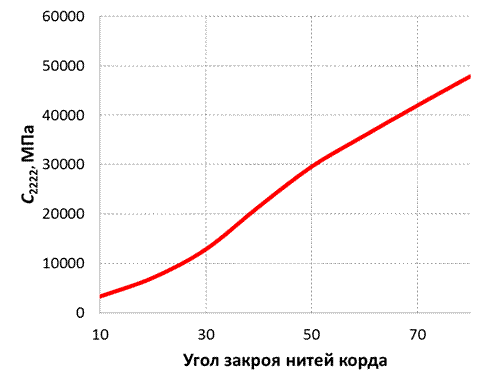
Рис. 5. Зависимость коэффициента C2222 от угла закроя нитей корда.
Если обратить внимание на графики зависимости коэффициентов C1111 и C2222 (отвечающих за поведение двуслойного резинокорда при растяжении) от угла закроя – мы увидим в первом случае монотонное убывание, во втором случае монотонное возрастание. Значения этих коэффициентов при угле закроя 10 градусов и при угле 80 градусов различаются примерно на порядок.
Что же касается зависимости для коэффициентов C1122 и C1212 (которые описывают поведение резинокорда при сдвиге) – графики получаются симметричными. Значения коэффициентов монотонно возрастают примерно до 45 градусов, затем монотонно убывают. Максимальные значения коэффициентов превышают минимальные в 2,5–3,5 раза.
Заключение
Результаты расчётов эффективных характеристик двуслойного резинокорда показывают, что этот материал является анизотропным [13]. Исходя из полученных графиков зависимостей, можно сделать выводы:
- если двуслойный резинокорд подвергается растяжению в определённом направлении (и необходимо усилить материал в этом направлении) – то нити корда в соседних слоях должны быть расположены возможно ближе к этому направлению (при этом угол между нитями в соседних слоях минимален);
- если двуслойный резинокорд подвергается сдвиговой нагрузке – угол между нитями корда должен быть возможно ближе к 45 градусам.
Работа выполнена при финансовой поддержке Минобрнауки России по государственному контракту № 07.524.11.4019 в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы».
Литература:
- Бидерман В.Л. и др. Автомобильные шины (конструкция, расчёт, испытание, эксплуатация). – М.: Госхимиздат, 1963. – 383 c.
- Бухин Б.Л. Введение в механику пневматических шин.- М: Химия, 1988, 224 с.
- Гамлицкий Ю.А., Левин В.А., Филиппенко Е.В., Яковлев М.Я. К вопросу о постановке задачи расчета поля напряжений элементарной ячейки эластомерного нанокомпозита. – Каучук и резина 2010, №4. С. 22-25.
- Гамлицкий Ю.А., Мудрук В.И., Швачич М.В., Бaсс Ю.П. Упругий потенциал наполненных резин // Каучук и резина 2002, № 3. С. 39-39.
- Дерлугян Ф.П. Композиционный полимерный тонколистовой материал (КПТМ) для работы в трибосопряжениях при экстремальных условиях [Электронный ресурс] // «Инженерный вестник Дона», 2007, №2. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2009/250 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Левин В. А., Калинин В. В., Зингерман К. М., Вершинин А. В. Развитие дефектов при конечных деформациях. Компьютерное и физическое моделирование. / Под ред. В. А. Левина. – М., Физматлит, 2007. – 392 с.
- Левин В.А., Лохин В.В., Зингерман К.М. Об одном способе оценки эффективных характеристик пористых тел при конечных деформациях // Изв. РАН/ Мех тв. тела. 1997. № 4. С 45-50.
- Левин В.А., Зингерман К.М. О построении эффективных определяющих соотношений для пористых упругих материалов при конечных деформациях и их наложении // Доклады РАН. 2002. Т. 382, № 4. С. 482-487.
- Логинов В.Т., Дерлугян П.Д. Химическое конструирование трибокомпозитов и их производство в ОКТБ «Орион» [Электронный ресурс] // «Инженерный вестник Дона», 2007, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2009/250 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Лурье А. И. Нелинейная теория упругости. М., Наука, 1980. – 512 с.
- Победря Б.Е. Механика композиционных материалов. — М.: Изд-во МГУ, 1984.-336 с.
- Седов Л.И. Введение в механику сплошной среды. — М.: Физматгиз, 1962. - 284 с.
- Черных К.Ф. Введение в анизотропную упругость. – М.: Наука, 1988. – 192 с.
- Яковлев М.Я. О численной оценке эффективных механических характеристик резинокордных композитов. // Вестник Тверского государственного университета, №17, 2012.
- Levin V.A., Zingermann K.M. Effective Constitutive Equations for Porous Elastic Materials at Finite Strains and Superimposed Finite Strains// Trans. ASME. Journal of Applied Mechanics. 2003. Vol. 70, No. 6. P.809–816.
- Levin V.A., Lokhin V.V., Zingerman K.M. Effective elasticproperties of porous materials with randomly dispersed pores. Finite deformation // Trans. ASME. J. Appl. Mech. 2000. V. 67, No. 4. P. 667-670.
- Zienkiewicz O.C., Taylor R.L. - Vol. 1. The finite element method. The basis, 2000, 707p.
- Zienkiewicz O.C., Taylor R.L. - Vol. 2. The finite element method. Solid mechanics, 2000, 479p.
- Официальный сайт ООО «Фидесис» [Электронный ресурс] – http://cae-fidesys.com