Модельная задача для поверхностей второго порядка положительной кривизны
Аннотация
Дата поступления статьи: 30.04.2013В работе изучаются бесконечно малые изгибания поверхностей положительной кривизны с краем, подчинённых на краю внешней связи смешанного типа. Устанавливается квазикорректность такой внешней связи при условии, что векторное поле принадлежит поверхности
Ключевые слова: поверхность положительной кривизны, бесконечно малые изгибания, поле смещений, поле вращений, собственное векторное поле, модельная задача
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Основная задача теории бесконечно малых изгибаний поверхностей состоит в отыскании нетривиальных полей смещений, удовлетворяющих основному уравнению dr̅dU̅ = 0, где r̅ – радиус-вектор точки поверхности, U̅ – поле смещений при бесконечно малом изгибании поверхности. Если поверхность подчинена тем или иным связям, то при интегрировании этого уравнения необходимо учесть также эти связи, то есть нужно отыскивать нетривиальные поля смещений, которые совместимы с наличными связями [1, c. 385]
Из основного уравнения следует, что dU̅=V̅×dr̅, где V̅ – некоторая вектор-функция, определяющая вращение при бесконечно малом изгибании поверхности некоторой её элементарной площадки. Векторное поле V̅ называют полем вращений [1, с.412]
При исследовании бесконечно малых изгибаний поверхностей с краем на поведение поверхности при деформации накладываются различные краевые условия. Обычно эти условия состоят или в ограничениях на способ изменения пространственного расположения края (кинематические связи) или же на характер изменения каких-либо геометрических характеристик поверхности вдоль края. Например, бесконечно малые изгибания скольжения относительно плоскости – это деформации, выражаемые краевым условием U̅n̅ = 0, где n̅ – нормаль плоскости. Если вдоль края ∂S поверхности S задано векторное поле l̅ и если деформации U̅ ищутся с краевым условием U̅l̅=c, где с − заданная вдоль границы поверхности скалярная функция, то говорят о бесконечно малых изгибаниях обобщенного скольжения. Если деформации поверхности ищутся с условием вида V̅n̅ = c, где n̅ − нормаль к поверхности, то говорят об условии обобщённого
Кроме того, рассматриваются и смешанные внешние связи вида
α(s)(U̅l̅)+β(s)(V̅n̅)=γ(s)
где U̅ и V̅ – векторные поля смещения и вращения бесконечно малого изгибания поверхности, l̅ – векторное поле, заданное вдоль края поверхности, n̅ – вектор нормали поверхности S, α (s), β (s), γ(s) – некоторые функции длины дуги s, заданные вдоль границы поверхно
Граничное условие (1) называется квазикорректным с р степенями свободы, если однородное условие (с=0) совместимо точно с р линейно независимыми бесконечно малыми изгибаниями поверхности S, а неоднородное условие совместимо с бесконечно малыми изгибаниями для любой функции с. Векторное поле l̅ называется собственным, если условие 11) не является квазикорректным [2, с. 152]
Пусть поверхность отнесена к некоторой системе координат x1, x2. Тогда векторы r̅α = ∂r̅ / ∂xα, =α=1,2) составляют базис координатной системы x1, x2. Удобно ввести также сопряжённый базис r̅α = gαβr̅β, ,α=1,2), где g11 = g22 / g, g12 = g21 = -g21/g, g22=g11 / g , величины gαβ и gαβ – контравариантные и ковариантные составляющие метрического тензора поверхности, g = g11g22 – g212 – дискриминант этой метрической формы. Далее, будем считать, что x1, x2 – сопряженно-изотермические параметр
В базисе (r̅i,n̅), i = 1,2 вектор смещения имеет разложение U̅ =uir̅i + u0n̅, i
Следуя [1, с.403] введём комплексную функцию изгибания w(z) = u1 + iu2.
Внешняя связь (1) для функции смещения w(z) записывается в виде:
Re{i∂zw+c1(z)w(z)}=γ1(s), z ∈ ∂D (2)
где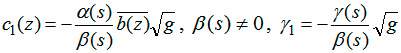 
.
Для однопараметрического семейства внешних связей
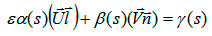(3)
где ε – вещественный параметр, ε ∈ (-∞,∞), получаем, что внешняя связь (1) запишется в виде:
Re{i∂zw+ εc1(z)w(z)}=γ1(s), z ∈ ∂D (4)
где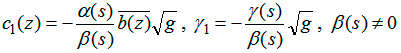 
.
Теорема. Пусть S – кусок поверхности второго порядка положительной кривизны K ≥ k0 > 0, S ∈ C3,μ , 0 < μ < 1 с краем ∂S, ∂S ∈ C2,μ, 0 < μ < 1, подчинённый на краю внешнему условию (3), где s ∈ ∂S, l̅ ∈ S, векторное поле l̅ и функции α, β, γ принадлежат классу Cμ , μ > 1. Тогда внешняя связь )3) квазикорректна с p = 3 степенями свободы для любого ε ∈ ∞-∞,∞) исключая быть может дискретный ряд значений ε1, ε2 ,… 0 < |ε1| < |ε2| < …
Доказательство: Рассмотрим однопараметрическое семейство задач
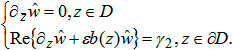(5)
к которому приводится краевое условие (3) (здесь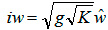 
).
Рассмотрим однородную задачу (5) (при γ2 = 0).
Обозначим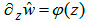 
, тогда получим
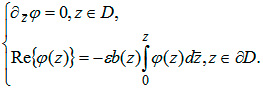(6)
Решение φ(z) принадлежит классу C1,μ(D + ∂D) и определяется по формуле:
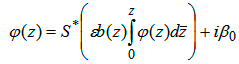(7)
где βo= β̅0 , S* - обобщённый оператор Шварца уравнения задачи 66) в области D.
Так как φ(z) ∈ C1,μ(D + ∂D), то искомая функция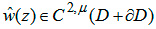 
и имеют место следующие равенства:
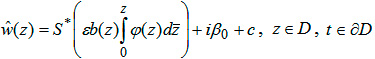(8)
где c - комплексная константа, а интегрирование производится по любой кривой, соединяющей начало координат с точкой z. Из равенства (8) следует, что решение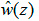 
зависит от p=3 констант.
Оператор S* отображает функции класса C1,μ(∂D) в функции класса C2,μ(D + ∂D). Так как область D ограниченная, а оператор Шварца S* непрерывный, то имеет место оценка:
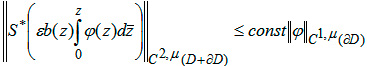(9)
где const не зависит от функции φ.
Оператор S* является вполне непрерывным. Поэтому уравнение (7) имеет отличные от нуля решения не более чем для счётного множества εk, k=1,2,… (0 < |ε1| < |ε2| < …). Таким образом, уравнение (7) разрешимо единственным образом для всех ε ≠ εk, k=1,2,… и для любой функции iβo + c.
Таким образом, краевая задача (6) является квазикорректной при n ≥ 0 для всех значений ε ∈ (-∞,+∞), за исключением, быть может, счётного множества εk, k=1,2,… Этим значениям соответствуют собственные векторные поля условия (3).
Результат, сформулированный в доказанной теореме, смоделирован автором для сферических сегментов и для параболоида вращения.
Литература
1.Векуа, И.Н. Обобщённые аналитические функции. М.: Физматлит, 1959.
2.Фоменко, В.Т. О квазикорректности внешних связей в теории бесконечно малых изгибаний //Сибирский математический журнал. 1974. Т.15. №1. – С.152-161.
3. Казак, В.В. Распределение собственных векторных полей условия обобщённого скольжения в нормальных сечениях //Мат. анализ и его приложения, РГУ. 1974. – С. 183-188.
4. Фоменко, В.Т. О жёсткости поверхностей с краем в римановом пространстве. // ДАН СССР. Том 187, №2. 1969. – С. 280 – 283.
5. Данилюк, И.И. О задаче с наклонной производной. // СМЖ. Том 3, №1. 1962. – С. 18 – 55.
6. Сабитов, И.Х. Бесконечно малые изгибания выпуклых поверхностей с краевым условием обобщённого скольжения // ДАН СССР. – 1962. – 147, №4. – С.793 – 796 (РЖМат, 1964, 10А419).
7. Nitsche Joachim. Beitrage zur Verbiegung zweifach zuaamtnenhangender Flachenstucke // Math. Z. – 1955. – 62, № 4. – C. 388 – 399 (РЖМат, 1956, 7587).
8. Grotemeyer К. Р. Einige Probleme und Methoden der Flachentheorie im Grossen // Math.-phys. Semesterber. – 1964. – 10, № 2. – С 187 – 201. (РЖМат, 1964, 10A419).
9. Литвинов, В.В., Кулинич И.И. Соотношения между компонентами поверхностной нагрузки в оболочках вращения при безмоментном их состоянии [Электронный ресурс] // «Инженерный вестник Дона», 2012, №3 (часть 2). – Режим доступа: http://ivdon.ru/magazine/archive/n3y2012/953 (доступ свободный) – Загл. с экрана. – Яз. рус.
10. Панасюк, Л.Н., Таржиманов, Э.А., Чантха Хо. Моделирование работы сооружений с учетом проявления неравномерных деформаций в основании [Электронный ресурс] // «Инженерный вестник Дона», 2011, №4. – Режим доступа: http://ivdon.ru/magazine/archive/n4y2011/591 (доступ свободный) – Загл. с экрана. – Яз. рус.