Диагностирование логического элемента DC LUT FPGA
Аннотация
Дата поступления статьи: 21.03.2014Предлагается модифицировать ранее предложенный логический элемент DC LUT ПЛИС типа FPGA путём введения дополнительных средств, позволяющих производить его «быстрое» диагностирование путём подачи тестового сигнала по всем ветвям дерева транзисторов. Для предложенной модификации выполнено моделирование, подтверждающее правильность ее функционирования, а также приведена оценка сложности в количестве используемых транзисторов.
Ключевые слова: логический элемент, ПЛИС FPGA, диагностирование, тестирование, надежность
05.13.05 - Элементы и устройства вычислительной техники и систем управления
Введение
В настоящее время программируемые логические интегральные схемы (ПЛИС) получили широкое распространение, например для разработки алгоритмов и моделей приема и обработки шумоподобных сигналов [1].
Логический элемент (ЛЭ) современных ПЛИС типа FPGA - LUT (Look Up Table) представляет собой мультиплексор в виде дерева передающих транзисторов, входы данных которого настраиваются так называемыми конфигурационными ячейками памяти - SRAM [2 - 4]. Как правило, в FPGA используются мультиплексоры на 4 - 5 переменных, уже применяются более мощные LUT на 6 - 7 переменных. С целью упрощения дальнейших рассуждений рассмотрим логический элемент ПЛИС типа FPGA на две входных переменные (LUT 2).
В [5 - 8] с целью упрощения реализации систем логических функций предложена структура, «обратная» структуре LUT 2 – дешифратор DC LUT 2 (рис. 1).

Рис. 1. – Транзисторная схема дешифратора DC LUT 2
При этом программируются связи выходов 0, 1, 2, 3 с соответствующими элементами «ИЛИ» с целью реализации систем логических функций.
С целью исключения состояний неподключенных входов выходных инверторов предложено для каждого выходного инвертора на рис.1 создать альтернативную цепочку, гарантированно переводящую его выход, например, в единицу. Для этого предлагается использовать выражение, двойственное конъюнкции, описывающей соответствующую цепочку в обратном дереве (рис. 2).

Рис. 2. – Нулевой разряд DC LUT 2 с альтернативной цепочкой
ПЛИС может рассматриваться как реконфигурируемая вычислительная система или как ее базовый модуль. Для таких систем принципиально важно уметь быстро определять работоспособное состояние эффективного функционирования [9]. Проверка работоспособности (диагностирование) как LUT, так и DC LUT является сложной задачей. В общем случае требуется проверить активирование всех 2n цепочек передающих транзисторов. Все наборы значений переменных надо загружать в ЛЭ и оценивать выходную реакцию LUT, а таких ЛЭ могут быть сотни тысяч.
Рассмотрим один из способов сокращения времени такого тестового диагностирования DC LUT с перспективой введения встроенных средств диагностики в ПЛИС FPGA для высоконадёжных, критических применений.
Моделирование ЛЭ LUT 2
Выполним моделирование ЛЭ LUT для n=2 в системе схемотехнического моделирования NI Multisim 10 фирмы National Instruments Electronics Workbench Group (USA, Austin) [10] (рис. 3).
Настройка моделируется ключами d3..d0. При установке адреса х2х1=00 ключами 1 и 2 на выходном инверторе наблюдаем z = 1, при этом 0 на вход инвертора поступает с входа d0. Если d0 устанавливаем в 1, то на выходном инверторе наблюдаем z = 0.
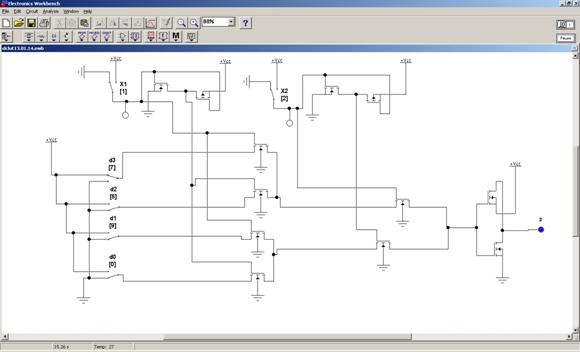
Рис. 3. – Моделирование ЛЭ LUT 2
Аналогично выполняем моделирование передачи настроечных сигналов со входов d1..d3. Результаты моделирования приведены в таблице №1.
Таблица №1.
Результаты моделирования ЛЭ LUT 2
Адрес в базе x2x1 |
Сигнал на входе |
Сигнал на выходном инверторе |
|
01 |
d1 = 0 |
z = 1 |
|
01 |
d1 = 1 |
z = 0 |
|
10 |
d2 = 0 |
z = 1 |
|
10 |
d2 = 1 |
z = 0 |
|
11 |
d3 = 0 |
z = 1 |
|
11 |
d3 = 1 |
z = 0 |
Таким образом, ЛЭ LUT2 функционирует правильно – реализует логическую функцию двух переменных, заданную настроечными входами d3..d0. Выполним «разворот» ЛЭ для реализации DC LUT2.
Моделирование ЛЭ DC LUT 2
На рис. 4 представлена упрощённая модель DC LUT 2 без альтернативных цепочек, то есть структура, «обратная» структуре LUT 2.
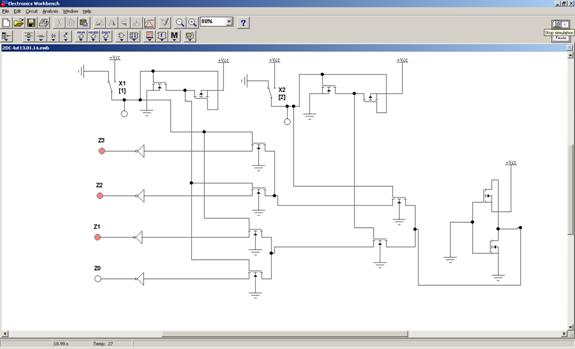
Рис. 4. – Дешифрация нулевого адреса
В этой схеме сигнал идёт в обратную сторону – с выхода инвертора на выходы z3..z0, причём для последних введены 4 дополнительных инвертора. Активирование в состояние нуля z3..z0 определяется адресом в базе х2х1. В КМДП транзисторах, используемых в LUT, при одинаковых топологических характеристиках стоки и истоки транзисторов фактически эквивалентны. Поэтому можно выполнять своего рода «реверс» сигналов.
Аналогично рис. 4 проверяем дешифрацию состояний 1, 2 и 3, устанавливая адрес в базе x2x1 равным 01, 10 и 11соответственно.
Таким образом, моделирование подтверждает правильность функционирования предложенного DC LUT.
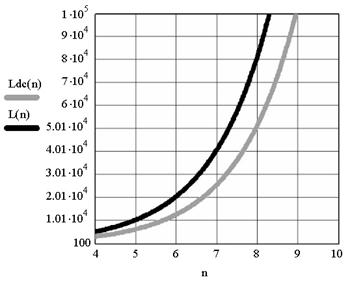
Сравним по сложности известный LUT (L(n)) и предложенный DC LUT (Ldc(n)) для реализации систем логических функций при различных значениях числа переменных n:
![]()
![]() (1)
(1)
где m – количество логических функций в системе, которое принимает значения 8, 16, 32. Графики зависимостей представлены на рис. 5.
Таким образом, получаем выигрыш в сложности порядка 30% и более, что может привести и к сокращению энергопотребления, и к повышению вероятности безотказной работы LUT при реализации систем логических функций.
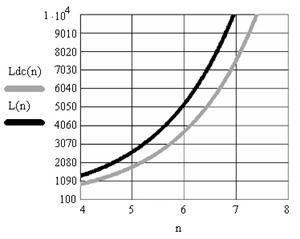
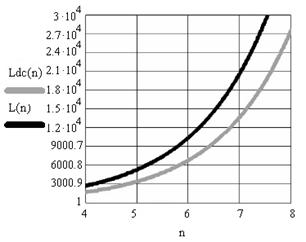
а) б)
 в)
в)
Рис. 5. – Сравнение аппаратных затрат в транзисторах известной структуры LUT – L(n) и DC LUT – Ldc(n) при а) m = 8, б) m = 16, в) m = 32
«Быстрое» диагностирование логического элемента DC LUT
Такое диагностирование обеспечим одновременной активацией всех ветвей обратного дерева DC LUT с помощью дополнительных транзисторов (рис. 6).
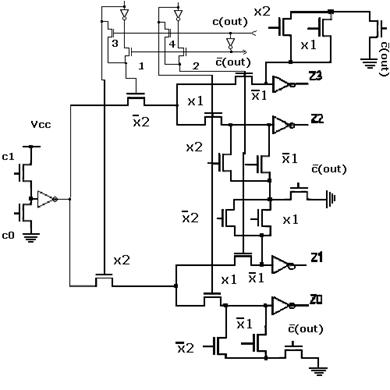
Рис. 6. – DC LUT 2 с альтернативными цепочками и дополнительными средствами «быстрого» диагностирования.
Функционирование и диагностика DC LUT для n=2 со средствами «быстрого» диагностирования описываются таблицей №2.
Таблица №2
Функционирование и диагностика DC LUT 2 со средствами «быстрого» диагностирования
х2 |
х1 |
c0 |
c1 |
c(out) |
|
z0 |
z1 |
z2 |
z3 |
Примечание |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
Основное функционирование DC LUT 2, дешифрация 0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
Основное функционирование DC LUT 2, дешифрация 1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
Основное функционирование DC LUT 2, дешифрация 2 |
|
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
Основное функционирование DC LUT 2, дешифрация 3 |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
«Быстрое» диагностирование DC LUT – тест «все единицы» |
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
«Быстрое» диагностирование DC LUT – тест «все нули» |
Моделирование «быстрого» диагностирования ЛЭ DC LUT
Моделирование «быстрого» диагностирования логического элемента DC LUT тестами «все единицы» и «все нули» было выполнено в системе схемотехнического моделирования NI Multisim 10.
Выполненное моделирование подтверждает правильность функционирования предложенного DC LUT со средствами «быстрого» диагностирования путём одновременной проверки всех ветвей обратного дерева передающих транзисторов.
Оценка сложности MDC LUT
Сравним сложность в числе транзисторов DC LUT на n переменных и m функций (1) и модифицированного для «быстрого» диагностирования MDC LUT – Lmdc(n) (2):
![]() (2)
(2)
Получим отношение сложностей (2) и (1):
![]()
При m = 16 получаем увеличение сложности порядка 1,5–2%, при m = 32 получаем относительное увеличение сложности ещё меньше.
Заключение
Предложенная реализация модифицированного MDC LUT для «быстрого» диагностирования ЛЭ ПЛИС FPGA требует избыточности менее 5% от объёма основного оборудования, причём эта доля снижается при увеличении n и m. Снижение быстродействия незначительно, дополнительная задержка составляет порядка нескольких передающих транзисторов, в приведённых примерах – всего один транзистор по данным и один по адресным сигналам. Проверка дерева передающих транзисторов двумя видами тестов «все единицы» и «все нули» занимает два такта, в отличие от прямой проверки каждой отдельной ветви на прохождение «нуля» и «единицы», занимающей 2n+1 тактов.
Введённые дополнительные технические средства MDC LUT могут обеспечить реализацию встроенных алгоритмов тестирования FPGA, что находится в «тренде» активно продвигаемого I-IP (Infrastructure Intellectual Property, так называемого встроенного сервисного обслуживания) и стандарта IEEE 1500, ориентирующего производителей ПЛИС на методы встроенного поиска неисправностей.
Для углублённой проверки DC LUT возможно дополнительное введение средств раздельного управления адресами.
Целесообразно в дальнейшем рассмотреть вопросы эффективного сочетания прямого и обратного («реверсного») диагностирования для более детальной диагностики ЛЭ ПЛИС FPGA.
Литература:
- Кузьмин Е.В., Зограф Ф.Г. Параметризованная модель генератора псевдослучайных последовательностей в OrCAD [Электронный ресурс] // «Инженерный вестник Дона», 2013, №3. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2013/1766 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Цыбин, С. Программируемая коммутация ПЛИС: взгляд изнутри. [Электронный ресурс] – Режим доступа: http://www.kit-e.ru/articles/plis/2010_11_56.php (доступ свободный) – Загл. с экрана. – Яз.рус.
- Tyurin S.F., Grekov A.V., Gromov O.A. The Principle of Recovery Logic Fpga for Critical Applications by Adapting to Failures of Logic Elements [Текст] // World Applied Sciences Journal, 2013. – Vol. 26 N 3. – P. 328-332.
- Zeidman, B. Designing with FPGAs and CPLDs [Текст] / B. Zeidman. – Lawrence, USA: CMP Books, 2002. – 241 p.
- Тюрин С.Ф., Сулейманов А.А., Городилов А.Ю. Системный синтез отказоустойчивых цифровых схем в функционально-полном толерантном базисе [Текст] // Нейрокомпьютеры: разработка, применение, 2013. – №11. – С. 82-88.
- Тюрин С.Ф., Сулейманов А.А., Городилов А.Ю. Отрицание дешифратора [Текст] // Нейрокомпьютеры: разработка, применение, 2013. – №11. – С. 59-63
- Городилов А.Ю., Понуровский И.С., Тюрин С.Ф. Повышение отказоустойчивости FPGA путём реконфигурации работоспособных элементов [Текст] // Радiоелектроннi i комп’ютернi системы, 2013. – № 1(60). – С. 172-176.
- Тюрин С.Ф., Понуровский И.С. Логический элемент ПЛИС FPGA для реализации ДНФ [Текст] // Вестник Ижевского государственного технического университета, 2013. – № 2. – С. 95-98.
- Строцев А.А., Андреев А.А. Оценка нахождения реконфигурируемой вычислительной системы в состояниях эффективного функционирования [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 1). – Режим доступа: http://ivdon.ru/magazine/archive/n4p1y2012/1212 (доступ свободный) – Загл. с экрана. – Яз. рус.
- NI Multisim [Электронный ресурс]. – Режим доступа: http://www.ni.com/multisim/ (доступ свободный) – Загл. с экрана. – Яз. англ.