Определение четко доминирующих тактик для выработки альтернативных управляющих решений в условиях полной неопределенности
Аннотация
Дата поступления статьи: 04.04.2014Статья посвящена моделированию процесса принятия решения в сложных системах в условиях полной неопределенности. Проблема формулируется на основе синтеза концепций теории управления и принятия решений, теории нечетких множеств и нечеткой логики, теории иерархических многоуровневых систем, теории полезности и теории игр, что расширяет возможности учета неопределенностей различной природы, естественным образом присущих математическому описанию окружающей действительности. Обозначены проблемы поиска решений в нечеткой иерархической системе управления. Предложен способ описания и нахождения альтернативных решений в многоуровневых сложных системах, основанный на обработке информации в виде нечетких интервалов с учетом двух видов политик консервативной и агрессивной на основе критериев maxmin и minmax. Приведен пример, демонстрирующий работу алгоритма выбора двух групп альтернатив на одном уровне иерархий целей в условиях полной неопределенности.
Ключевые слова: Сложная система; принятие решения, нечеткий интервал, управляющее решение; полная неопределенность
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Введение
Актуальность представленной работы обоснована возросшим требованием учета человеческого фактора при разработке моделей для выработки оптимальных управляющих решений. В большинстве случаев решение принимается аналитиком или экспертом исключительно исходя из субъективного оценивания ситуации и в условиях частичной или полной неопределенности. Поэтому разработка методов и подходов формализации принятия решения по управлению сложноформализуемыми динамическими ситуациями с учетом человеческого фактора является актуальной.
Большинство предлагаемых подходов в разработке методов поддержки принятия решений не позволяют однозначно определить стратегию управления по достижению поставленной цели [1].
Предположим, что лицо, принимающее решение (ЛПР), в сложных условиях должно сделать выбор среди возможных действий, носящих важный социально-экономический характер. Предположим также, что проблема, для которой выбирается наилучший способ решения сложна, для ее анализа уже построена имитационная модель, реализованная с помощью ЭВМ подобно [2], и это позволяет выработать множество альтернативных вариантов действий, составить сценарий возможного развертывания событий в будущем, но не позволяет определить однозначно тактику действий. Например, в [3] предлагается использовать статический анализ для решения этого вопроса, но такой подход не позволяет учитывать показатели разной природы. Интересны подходы по получению знаний в условиях многокритериальности и неопределенности, изложенные в [4 − 7], однако в них не всегда учитывается возможность коалиции.
Анализ проблемы
С точки зрения теории полезности фон Неймана–Моргенштерна [8] и в соответствии с понятием «рационального» поведения, ЛПР следует подобрать для каждого исхода такое число, называемое полезностью этого последствия, которое удовлетворяло следующему. Чем более предпочтителен некоторый набор значений показателей, тем выше его полезность. Лучшая альтернатива оценивается максимальной полезностью.
Чтобы дать оценку относительной желательности данной альтернативы действий, нам необходимо последовательно, для каждого конкретного эксперимента, получить соответствующее последствие, каждому из которых поставить в соответствие численное значение его полезности; найти среднее (ожидаемое) значение полезности для последовательности последствий, получаемых в результате многократного повторения эксперимента, что позволит выбрать такую альтернативу действий, которая обеспечит максимум ожидаемой полезности.
Для учета неопределенностей, необходимо установить значения вероятности для каждой из альтернатив путем использования или эмпирических данных, или результатов различных стохастических и динамических моделей, мнения экспертов. После того как ЛПР формализует свою проблему, установит соответствующие значения вероятности и полезности, оптимальная альтернатива может быть найдена с помощью вычислений – оптимальной будет стратегия, которая максимизирует ожидаемую полезность.
Проблема в том, что единственное выбранное четкое число не сможет отобразить всю описательную составляющую сложной системы, а увеличение количественных характеристик приведет к возрастанию числа комбинаций (переборов) в зависимости от каждой из характеристик.
Обоснование применения интервального оценивания
Решение обозначенных проблем видится в применении модели управления, использующей нечеткую логику для выработки альтернативных управляющих решений и выбора из них оптимального. Такие нечеткие динамические модели находят применение при моделировании и исследовании систем и процессов различной природы: технических, политических, экологических, химических, медицинских, социально-экономических, геоинформационных и др., т.е. сложных систем.
Чаще всего лицо, ЛПР пытается навязать свой опыт противоположной стороне в ситуациях, когда одна из сторон обладает значительным опытом и интуицией по принятию решения в «знакомых» ему ситуациях. Для этого перед противодействующей стороной ставятся такие проблемы, которые, по мнению первой, могут повысить приобретаемое качество с минимумом затрат. Поскольку противоположная сторона может противиться необходимости решения проблем предлагаемой сложности и объема, то между сторонами совершается своеобразный торг за оценку приращения показателя качества в случае решения проблемы. Обе стороны пытаются «сойтись» на одном числе, но чаще всего это не удается, выход – в выборе некоторого интервала оценок. Что и приводит к нечеткой оценке решения в виде интервального оценивания. Поэтому в качестве инструментария для обработки неопределенных данных выбран метод, основанный на определении и сравнении нечетких интервалов с их границами.
Предлагается следующий комплекс взаимодействующих моделей для решения проблем многоэтапности, коллективности и предпочтения ЛПР, который включает в себя: модели динамики нарастания показателя, характеризующего качество функционирования системы; игровые модели, в которых в зависимости от способа описания исходов взаимодействия и полноты информации, производится поиск единственного или нескольких допустимых исходов с точки зрения желаемого уровня достижения цели; ситуационную модель сценария игры, в которой динамическое изменение класса стратегий происходит в зависимости от полезности предшествующих взаимодействий в условиях нечеткой и неполной информации; модели прогноза достижимости конечной цели при применении управлений с различной силой воздействия на величину приращения показателя необходимого качества; модели принятия решений при многих критериях при поиске равновесных решений нечетких игр.
Чаще всего моделируется ситуация, когда решение первоначальной проблемы достигнуто, как только решены все подпроблемы. Однако, в условиях неопределенности достигнуть такого результата затруднительно, или приходится упрощать ситуацию. Использование интервального оценивания для каждой проблемы позволяет привести разбиение первоначально высокого уровня неопределенности информации, необходимой для решения проблемы, к множеству более мелких неопределенностей. Поэтому в данной работе и предлагается использовать алгоритм, позволяющий четко определить альтернативные управляющие решения с помощью нечетких интервалов.
Такую иерархию проблем принято называть иерархией слоев принятия решений [9], а всю систему − многослойной системой принятия решений, рис. 1, где Si является решающей подсистемой и/или ситуацией.
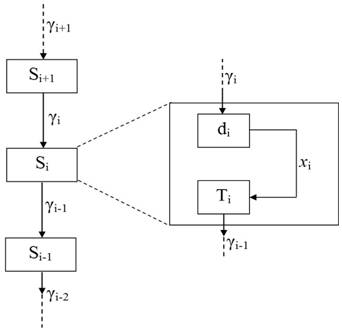
Рис 1. − Многоуровневое представление решающих подсистем
Будем использовать метод, описанный в [10], позволяющий определить параметры функции принадлежности ![]() произвольного нечеткого интервала
произвольного нечеткого интервала ![]() в виде трапеции с вычисленными левой и правой границами:
в виде трапеции с вычисленными левой и правой границами: 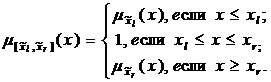
Иными словами, он позволяет вычислять наклоны левой и правой сторон трапеций, которые соответствуют лингвистическим понятиям, например, «около интервала 15-20», «около интервала 5-15» и «около интервала 1-5». Данный метод заложен в идею описываемого алгоритма.
Определим, что исход по каждой альтернативе (или выигрыш) определяется нечетким подмножеством w. Желаемый уровень выигрыша будем называть нечетким, если он определяется также в виде нечеткого подмножества (или интервала), например «в пределах от 5 до 20».
Алгоритм определения четко доминирующих тактик
Опишем работу предлагаемого алгоритма на примере. Некоторая целевая подсистема Si, представленная на рис. 1, характеризуется 10 признаками, и, соответственно, имеет 10 исходов ![]() , представленных в виде нечетких интервалов. Каждый исход аппроксимируется S-образной функцией принадлежности, тогда полезность нечеткой оценки исхода
, представленных в виде нечетких интервалов. Каждый исход аппроксимируется S-образной функцией принадлежности, тогда полезность нечеткой оценки исхода ![]() обозначим как
обозначим как ![]() , где
, где ![]() есть нечеткое подмножество отрезка [0,1] с функцией принадлежности:
есть нечеткое подмножество отрезка [0,1] с функцией принадлежности: 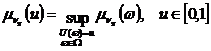 .
.
1. На первом этапе необходимо составить таблицу соответствия. В таблице 1 приведены примеры описания представители одного класса полезности типовых управляющих воздействий различной силы, отображаемые надстрочным индексом в интервале оценок, выявленные в ходе экспертного опроса.
Таблица № 1
Таблица соответствий
Последовательность управляющих решений (УР) |
Интервал оценок |
|
УР 1 |
|
|
УР 2 |
|
|
… |
… |
|
УР 10 |
|
2. Необходимо обработать данные письменного опроса представителей одинакового по требованиям класса о полезности их решений, таблица 2.
Таблица № 2
Таблица для обработки данных
Класс опрашиваемого |
Полезности, названные опрошенными |
||
|
УР 1 |
… |
УР 10 |
|
|
Слабый |
0,41 |
… |
0,62 |
|
Слабый |
0,45 |
… |
0,60 |
|
… |
… |
… |
… |
3. По каждому управляющему решению рассчитывается среднее арифметическое значение полезности.
4. На основании данных, полученных в п.3 строится график зависимости ![]() .
.
5. Для интервалов, где нет перекрытий интервалов с различающимися оценками полезности, функция полезности соответствует рассчитанному в п.3 значению. В местах перекрытия оценок полезности на одном интервале ![]() , она считается так же, как у самой слабой (по предпочтению) оценки на интервале, т.е.
, она считается так же, как у самой слабой (по предпочтению) оценки на интервале, т.е. ![]() , где
, где ![]() - усредненная полезность последовательности
- усредненная полезность последовательности ![]() управляющих решений, составляющих тактику
управляющих решений, составляющих тактику ![]() опрашиваемых лиц.
опрашиваемых лиц.
Экспертным методом получена совокупность нечетких оценок десяти исходов со «средними» способностями к приобретению заданного качества, использующего управления «средней» силы в виде нечетких интервалов, которые сведены в таблицу 3.
Таблица № 3
Нечеткие оценки исходов
|
нечеткий интервал |
|
нечеткий интервал |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
0 |
6. С помощью отображения найдем нечеткие интервальные оценки полезности ![]() ,. Ввиду ограниченности объема публикации представим сразу готовую таблицу 4 полученных нечетких оценок полезности, графическая интерпретация и правила отображения которых, подробно описаны в [11].
,. Ввиду ограниченности объема публикации представим сразу готовую таблицу 4 полученных нечетких оценок полезности, графическая интерпретация и правила отображения которых, подробно описаны в [11].
Таблица № 4
Таблица нечетких оценок полезности
|
нечеткий интервал |
|
|
|
нечеткий интервал |
|
|
|
|
|
[0.685; 0.79] |
(u; 0.67, 0.7) |
(u; 0.74, 0.84) |
|
[0.455; 0.68] |
(u; 0.24, 0.67) |
(u; 0.68, 0.68) |
|
|
[0.685; 0.8] |
(u; 0.67, 0.7) |
(u; 0.7, 0.9) |
|
0 |
|
|
|
|
[0.45; 0.8] |
(u; 0.31, 0.7) |
(u; 0.8, 0.8) |
|
[0.48; 0.8] |
(u; 0.29, 0.67) |
(u; 0.9, 0.7) |
|
|
0 |
|
|
|
0 |
|
|
|
|
[0.23; 0.46] |
(u; 0.2, 0.26) |
(u; 0.66, 0.26) |
|
0 |
|
|
7. Необходимо сопоставить полученные нечеткие оценки полезности исходов для ЛПР ![]() с предполагаемыми исходами окружающей среды
с предполагаемыми исходами окружающей среды ![]() , таким образом, мы получаем классический случай игры с двумя игроками. В результате применения критерия maxmin, таблица 5 и minmax, таблица 6, мы получим две группы четко доминирующих тактик.
, таким образом, мы получаем классический случай игры с двумя игроками. В результате применения критерия maxmin, таблица 5 и minmax, таблица 6, мы получим две группы четко доминирующих тактик.
Таблица № 5
Решения, полученные в результате применения критерия maxmin
|
|
|
|
|
|
|
|
|
|
|
|
Min |
|
|
0 |
0 |
0 |
|
0 |
0 |
|
0 |
|
|
0 |
|
|
0 |
[0.46;0.68] |
[0.69;0.79] |
|
[0.48;0.8] |
[0.48;0.8] |
|
[0.76;0.8] |
|
|
[0.46;0.68] |
|
|
[0.23;0.46] |
[0.48;0.8] |
[0.69;0.8] |
|
[0.48;0.79] |
[0.685;0.8] |
|
[0.72;0.82] |
|
|
[0.23;0.46] |
|
|
[0.23;0.46] |
[0.23;0.69] |
0 |
|
[0.48;0.8] |
[0.48;0.8] |
|
[0.72;0.82] |
|
|
[0.23;0.46] |
|
|
[0.23;0.68] |
[0.46;0.8] |
[0.69;0.79] |
|
[0.68;0.79] |
[0.76;0.8] |
|
[0.72;0.75] |
|
|
[0.23;0.68] |
|
|
[0.48;0.68] |
[0.69;0.79] |
[0.76;0.8] |
|
[0.69;0.79] |
[0.72;0.82] |
|
[0.69;0.75] |
|
|
[0.48;0.68] |
|
|
|
[0.46;0.68] |
[0.46;0.68] |
|
|
[0.76;0.8] |
|
0 |
|
|
[0.46;0.68] |
|
|
|
[0.48;0.8] |
[0.48;0.8] |
|
|
[0.8;0.82] |
|
0 |
|
|
[0.48;0.8] |
|
|
|
[0.69;0.79 |
[0.69;0.82] |
|
|
[0.72;0.82] |
|
0 |
|
|
[0.69;0.79] |
|
|
|
|
|
|
|
[0.48;0.8] |
|
[0.48;0.8] |
|
|
[0.48;0.8] |
Получаем единственное решение для ЛПР ![]() =[0.69;0.79].
=[0.69;0.79].
Таблица № 6
Решения, полученные в результате применение критерия minmax
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
0 |
|
0 |
|
|
|
|
0 |
[0.46;0.68] |
[0.69;0.79] |
|
[0.48;0.8] |
[0.48;0.8] |
|
[0.76;0.8] |
|
|
|
|
[0.23;0.46] |
[0.48;0.8] |
[0.69;0.8] |
|
[0.48;0.79] |
[0.69;0.8] |
|
[0.72;0.82] |
|
|
|
|
[0.23;0.46] |
[0.23;0.69] |
0 |
|
[0.48;0.8] |
[0.48;0.8] |
|
[0.72;0.82] |
|
|
|
|
[0.23;0.68] |
[0.46;0.8] |
[0.69;0.79] |
|
[0.68;0.79] |
[0.76;0.8] |
|
[0.72;0.75] |
|
|
|
|
[0.48;0.68] |
[0.69;0.79] |
[0.76;0.8] |
|
[0.69;0.79] |
[0.72;0.82] |
|
[0.69;0.75] |
|
|
|
|
|
[0.46;0.68] |
[0.46;0.68] |
|
|
[0.76;0.8] |
|
0 |
|
|
|
|
|
[0.48;0.8] |
[0.48;0.8] |
|
|
[0.8;0.82] |
|
0 |
|
|
|
|
|
[0.69;0.79] |
[0.69;0.82] |
|
|
[0.72;0.82] |
|
0 |
|
|
|
|
|
|
|
|
|
[0.48;0.8] |
|
[0.48;0.8] |
|
|
|
Max |
[0.48;0.68] |
[0.69;0.79] |
[0.69;0.82] |
|
[0.69;0.79] |
[0.72;0.82] |
|
[0.76;0.8] |
|
|
В данном случае получили две нечетко доминирующие тактики ![]() =[0.76;0.8] и [0.72;0.82], из которых надо выбрать одну. Для этого переходим к п.8.
=[0.76;0.8] и [0.72;0.82], из которых надо выбрать одну. Для этого переходим к п.8.
8. Алгоритм сравнения нечетких множеств был подробно описан в [12]. Применяя его для сравнения ![]() =[0.72;0.82] и
=[0.72;0.82] и ![]() =[0.76;0.8], получаем, что в условиях применения критерия minmax решением будет [0.76;0.8].
=[0.76;0.8], получаем, что в условиях применения критерия minmax решением будет [0.76;0.8].
Заключение
Преимущество описываемой иерархической структуры вложенных целевых подсистем состоит в ее устойчивости и гибкости по природе. Иерархические системы эволюционируют быстрее. Введение интервальной оценки позволяет проводить качественный анализ с учетом различной природы показателей и различия в силе связей между объектами системы, в отличие от четкого оценивания. Нечетко-множественные модели достаточно просты в построении и дают высоко-достоверные результаты даже в условиях неопределенности.
Как видно из примера, оценка выигрышей нечеткими числами с несимметричной функцией принадлежности позволяет сократить количество оптимальных альтернатив достижения конечной цели.
В отличие от известных работ, в данной – предлагается за счет использования нечетких интервалов учитывать лингвистическую структуру человеческих знаний, а применение специальных критериев позволяет оценить несовпадающие взгляды ЛПР на оценку приращения показателя качества функционирования системы.
Литература:
- Кулинич, А.А. Компьютерные систем анализа ситуаций и поддержки принятия решений на основе когнитивных карт: подходы и методы [Текст] // Проблемы управления. − 2011. − №4, − С.31 − 45.
- Влацкая, И.В., Нестеренко, М.Ю., Полежаев, П.Н. Модели поддержки принятия решений в условиях неопределенности, сводящиеся к кооперативным играм / [Текст] // Вестник Оренбургского государственного университета. − 2012. − №9(145), С.143 − 149.
- Kumar, Das S., Paul, A., Pradhan, A., Singh, R.K., Ghantasala, S.R. Use of statistical analysis for evaluating complex data of a steel making model developed for control of end point [Text] // International Journal of Ecology and Development. – 2013. – Vol 26, Is.3, pp. 37 – 49.
- Merad, M., Dechy, N., Serir, L., Grabisch, M., Marcel, F. Using a multi-criteria decision aid methodology to implement sustainable development principles within an organization [Text] // European Journal of Operational Research. − 2013. − Vol. 224, Is.3, pp. 603 − 613.
- Rusu, O., Halcu, I., Grigoriu, O., Neculoiu, G., Sandulescu, V., Marinescu, M., Marinescu, V. Converting unstructured and semi-structured data into knowledge [Electronic resources] // RoEduNet 11th Intern. Conf.: Networking in Education and Research; Romania; 17 − 19 Jan 2013 Access mode: http://conference.roedu.net/index.php/roedunetconf/roedunet11 Article № 6511736.
- Антонова, А.С., Аксенов, К.А. Многокритериальное принятие решений в условиях риска на основе интеграции мультиагентного, имитационного, эволюционного моделирования и численных методов [Электронный ресурс] // «Инженерный вестник Дона». – 2012. № 4 (часть 2). − Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1466 (доступ свободный) − Загл. с экрана. – Яз. рус.
- Побегайлов, О.А. Выработка решений в период кризиса и условиях неопределенности [Электронный ресурс] // «Инженерный вестник Дона». – 2013. № 2. − Режим доступа: http://www.ivdon.ru/magazine/ archive/n2y2013/1730 (доступ свободный) − Загл. с экрана. – Яз. рус.
- Кини, Р.Л., Райфа, X. Принятие решений при многих критериях: предпочтения и замещения: Пер. с англ. [Текст]: Монография /Под ред. И.Ф. Шахнова. – М.: Радио и связь, 1981. – 560 с.
- Vovk, S.P., Ginis, L.А. Modelling and forecasting of transitions between levels of hierarchies in Difficult formalized systems [Text] // European Researcher. − 2012. − Vol. (20), №5-1, − P.541-545.
- Bozhenyuk, A., Bershtein, L., Rozenberg, I. Maghout method for determination of fuzzy antibase set of fuzzy interval graph [Text] // Proceeding 19th International Conference on Soft Computing MENDEL 2013, Brno, Czech Republic, June 26 – 28, – 2013. pp. 253 – 258.
- Вовк, С.П. Ситуационное управление и нечеткие игры в моделировании организационных систем [Текст]: Монография / С.П. Вовк. − Таганрог: Изд-во ТРТУ, 2002, − 96 с.
- Вовк С.П., Гинис, Л.А. Моделирование переходов между эталонными ситуациями в сложных системах в условиях неопределенности [Текст] // Известия ЮФУ. Технические науки. − 2013. − №2. – С. 116 – 122.