Измерение тензорных величин магнитного поля в микроструктурном анализе ферромагнитных материалов
Аннотация
Описан способ позволяющий поднять качество магнитного метода технической диагностики. Для обнаружения дефектов исследуется топология производных компонент магнитного поля рассеяния структурных неоднородностей в ферромагнитных материалах. В качестве чувствительного элемента используется преобразователь Холла.
Ключевые слова: Дефектоскопия, неразрушающий контроль, микроструктурный анализ, тензорные компоненты, преобразователь Холла.
Технический контроль большинства ферромагнитных изделий производится в приложенном магнитном поле. При этом допускается, что предыдущее магнитное состояние изделия не влияет, или почти не влияет, на формирование полей дефектов, находящихся в изделии [1]. Намагничивание изделий приводит к потере структуры магнитного поля, сложившейся в результате действия нагрузок, износа, а также первичных полей дефектов.
Поля дефектов ферромагнитного изделия, находящегося в поле Земли, имеют особую структуру, т.к. формируются так называемыми объёмными зарядами. Вклад этих зарядов в общее поле изделия ощутим только в слабых полях, при намагничивании изделия до состояния, пригодного для классического магнитного контроля – состояния технического насыщения, основными источниками полей дефектов становятся поверхностные заряды [2, 3].
Технический контроль можно осуществлять и в поле Земли, не прибегая к дополнительному намагничиванию, и такой подход имеет ряд преимуществ: появляется возможность контролировать износ и «усталость» металла, которые ещё не привели к образованию дефектов, структуру металла для определения его качества, исключаются затраты на подготовку изделия до контроля и после него.
Рассмотрим задачу нахождения поля дефекта в плоскопараллельной пластине, которая хорошо изучена [4]. В качестве модели дефекта используется щель бесконечная по оси z, с шириной 2b, глубиной залегания h1, высотой h=h2 – h1 (рис. 1). Задача рассматривается в рамках дипольного приближения [5].
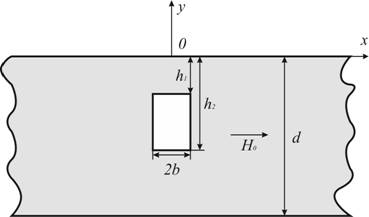
Рис. 1. Дефект в плоскопараллельной пластине
Составляющие магнитного поля удобно представить в виде комплексных величин![]() ,
, ![]() .
.
Магнитное поле N дефектов в воздухе можно представить в виде суммы полей создаваемых отдельными дефектами:![]() , (1)
, (1)
но так как дефекты воздействуют друг на друга, невозможно аддитивным сложением получить результирующее поле – нужно ввести поправки, описывающие взаимодействие. Поле одного дефекта можно записать в виде [4]![]() , (2)
, (2)
где TFj(z) ‑ топографический фактор j-го дефекта, σj – плотность магнитных зарядов на гранях j-го дефекта, с учётом влияния остальных дефектов. Топографический фактор содержит информацию о геометрии дефекта и его положении, плотность магнитных зарядов определяется размером дефекта, внешним полем и характеристиками материала. Будем рассматривать только один дефект, считая, что окружающие дефекты находятся на большом расстоянии и не оказывают никакого влияния.
Топографический фактор и плотность зарядов определяются из следующих выражений [4]:
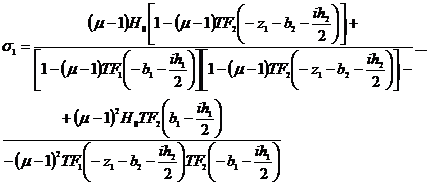 ,
,
(3)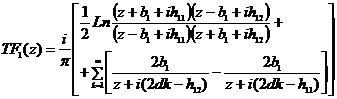 . (4)
. (4)
Расчеты магнитных полей по формулам (1) – (4) производились в системе Mathcad. На рис. 2 представлен график тангенциальной Bx(x, 0) компоненты магнитного поля для дефекта с параметрами 2b= 0,002 мм, h1 = 0,8 мм, h2 = 0,99 мм, d = 1 мм, во внешнем поле Н0 = 40 А/м, при магнитной проницаемости материала μ = 5000. Значение поля выбрано из расчёта среднего значения магнитного поля Земли. Из рис. 2 видно, что топология поля дефекта имеет явно выраженный дипольный характер.
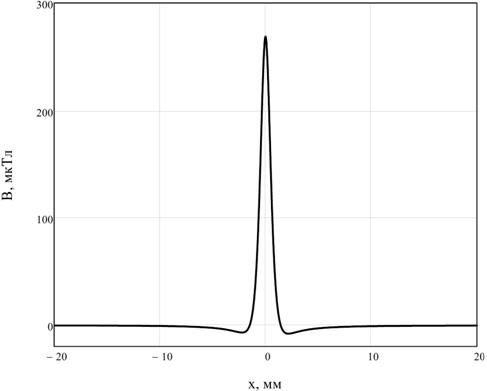
Рис. 2. Топология магнитного поля модели дефекта
Для подтверждения результата расчётов был создан искусственный дефект с подобными характеристиками. Для этого в стальной пластине была прорезана тонкая канавка, к этой пластине со стороны канавки плотно прижата такая же пластина. При этом канавка находится между слоями металла и её можно считать внутренним дефектом. Регистрация поля рассеяния искусственного дефекта проводилась с помощью холловского магнитометра [6] с использованием метода повешения чувствительности преобразователя Холла [7]. Результаты эксперимента приведены на рис. 3. Различие в пиковых значениях поля полученного в численном и натурном эксперименте обуславливается тем, что расчётное поле получено на поверхности пластины, а реальный датчик находится на некотором расстоянии от неё, а также различием в значениях поля Земли Н0 и магнитной проницаемости исследуемого материала μ.
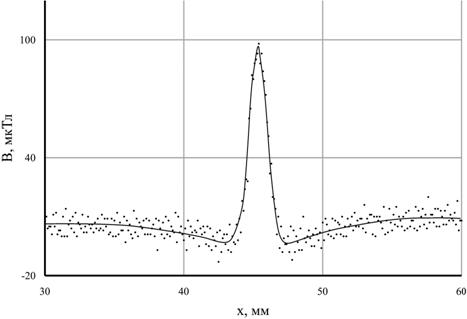
Рис. 3 . Топология магнитного поля реального дефекта
Для того чтобы повысить пространственное разрешение и чувствительность технического контроля в поле Земли, необходимо привлечь дополнительную информацию о поле дефекта, исследуя его пространственные производные. Для магнитного поля в свободном пространстве существует 5 независимых компонент тензора второго ранга первых производных вида ∂Bi/∂rj
Так как в слабых полях намагниченность материала вблизи дефекта изменяется резко, топология производных компонент поля рассеяния дефекта будет более информативна по сравнению с топографией самих компонент [5].
Для регистрации этих производных используется тензорный магнитометрический датчик, в котором преобразователи Холла расположены в вершинах равнобедренного треугольника (рис. 4).
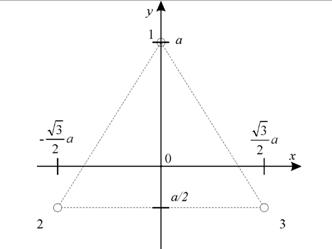
Рис. 4 – Схема тензорного магнитометрического датчика
В качестве меры дефекта можно использовать величину![]() , (5)
, (5)
где Bi – значения поля в точках 1, 2 и 3, совпадающих с центрами преобразователей Холла. В зависимости от ориентации преобразователей Холла в тензорном магнитометрическом датчике измеряемыми величинами B1, B2, B3 могут быть как нормальные, то есть By компоненты индукции, так и тангенциальные, то есть Bx.
На рис. 5 приведена топология тангенциальной компоненты тензорной меры (5), при а = 5,8 мм. Дефекты расположены на расстоянии 3 мм друг от друга, на разной глубине.
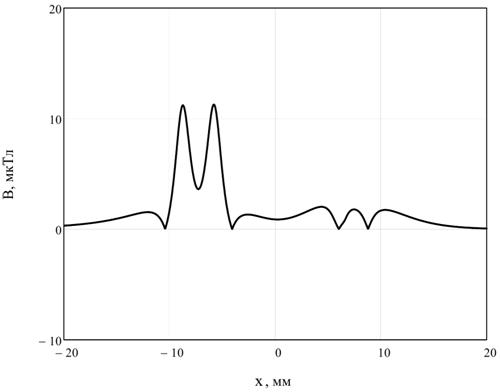
Рис. 5 – Топология тангенциальной компоненты тензорной меры
На рис. 6 изображена топология тангенциальной компоненты магнитного поля, сплошная линия – топология поля на поверхности пластины, пунктирная – на высоте 2 мм от поверхности. Как видно из рис. 6 топология скалярных компонент поля близкорасположенных дефектов не позволяет их разрешать.
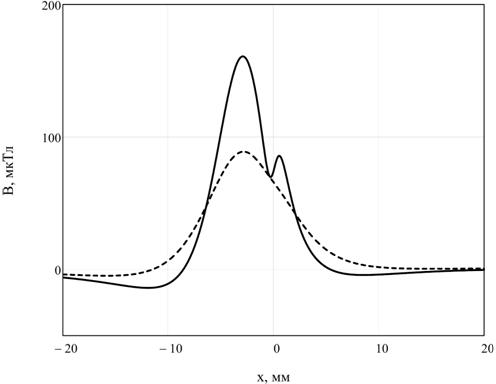
Рис. 6 – Топология тангенциальной компоненты магнитного поля
Таким образом, привлечение дополнительной информации в виде тензорных величин магнитного поля позволяет увеличить разрешающую способность магнитного метода технического контроля, а также качество получаемых магнитных образов дефектов. Эти преимущества позволяют производить анализ микроструктуры ферромагнитных материалов.
Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы (государственный контракт № 14.740.11.0830).
Литература:
- 1.Загидулин Р. В. Расчет остаточного магнитного поля дефекта сплошности в ферромагнитном изделии. I. Магнитное поле внутри ферромагнетика. // Дефектоскопия. – 1998. – № 10. – С. 21 – 32.
2.Загидулин Р.В. Некоторые особенности топографии магнитных полей дефектов сплошности // Дефектоскопия. – 1995. – №9. – С. 55-62.
3.Загидулин Р.В., Мужицкий В.Ф., Савенков Д.В. Влияние толщины пластины на магнитное поле дефекта сплошности // Дефектоскопия. – 1999. – №7. – С. 50-57.
4.Загидулин Р.В., Мужицкий В.Ф., Курозаев В.П. О разрешении дефектов сплошности по топографии магнитного поля // Дефектоскопия. – 2000. – № 5. – С. 46 – 56.
5.Янус Р. И. Некоторые вопросы теории магнитной дефектоскопии // ЖТФ. – 1945 – Т. 15. – № 1-2. С. 3 – 14.
6.Голубев А. А., Игнатьев В. К. Цифровой нанотеслометр // Известия ВУЗов. Приборостроение. – 2010. – Т. 53. – № 1. – С. 49 – 54.
7.Игнатьев В. К., Протопопов А. Г. Повышение разрешающей способности магнитометра на основе эффекта Холла // Известия ВУЗов. Приборостроение. – 2003. – Т. 46. – № 3. – С. 38 – 44.