Обработка диагностической информации при оценке технического состояния электроприводной арматуры АЭС
Аннотация
Когда применение контактных методов затруднительно, оценка состояния арматуры, снабженной электродвигателем, производится по сигналу тока двигателя. При анализе сигнала тока возникает задача выделения информативных составляющих на фоне помехи. В данной статье предлагается обработка диагностической информации, представленной в сигнале тока двигателя арматуры. Предлагаемые авторами методы обработки диагностической информации позволяют более точно установить состояние диагностируемого оборудования, чем применяемые в данной области штатные методы.
Ключевые слова: техническая диагностика, обработка сигналов, демодуляция, спектральный анализ, фазовый портрет.05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
При диагностировании роторного оборудования и, в частности, электроприводной арматуры (ЭПА), наиболее распространенным способом получения информации о техническом состоянии объекта является анализ виброакустического сигнала[1].
Источниками повышенной вибрационной активности являются колебания неисправных деталей редуктора. Данные колебания распространяются по кинематической цепочке редуктора, вызывая модуляцию вращения валов. Результирующее колебание зависит от характера неисправности[1,2]. Дефекты типа заклинивания, наиболее часто возникающие при неправильной сборке редуктора, характеризуется распространением крутильного колебания:
θ – угол поворота сечения; J – момент инерции, приложенные к валу; М(х,t) – крутящий момент; G – модуль сдвига вала; С – скорость распространения колебания; μ – коэффициент Пуассона. Дефекты, приводящие к усиленным соударениям в редукторе, возникающие при эксплуатационных дефектах подшипников и/или передач, проявляются как поперечные колебания:
![]() (2)
(2)
ξ – перемещение сечения вала вдоль координаты x; P(x, t) – внешние силы, приложенные к валу; Е – модуль Юнга; h –длинна вала.
Для анализа диагностических сигналов целесообразно использование графических методов. Наиболее распространенным в области технической диагностики способом обработки сигнала является разложение в ряд Фурье с последующим анализом спектра.
В соответствии с экспериментальными данными, в спектре сигнала исправной ЭПА могут наблюдаться первая гармоника вращения ротора fвр и сетевая гармоника fс, появление в спектре других гармоник свидетельствует о неисправности ЭПА. Так, в спектре виброакустического сигнала ЭПА с дефектом подшипника редуктора (рисунок 1) проявляются гармоники дефектного подшипника: 8,7; 32; 52; 91 - частоты сепаратора, тел качения, наружного и внутреннего колец соответственно.
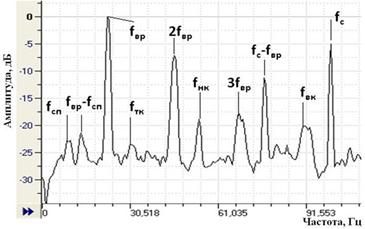
Рис. 1 Спектр виброакустического сигнала ЭПА с дефектом подшипника редуктора (fвр – частота вращения ротора, fс – вторая сетевая гармоника, fтк, fсп, fвк, fнк – частоты тел качения, сепаратора, внутреннего и наружного кольца подшипника).
I(t)=I0(1+I/p(t,Iz(t)))cos(we)
В данном сигнале номинальный рабочий ток двигателя I0, и сетевая гармоника ωe не несут диагностической информации. Функция перемещений ротора I/p(t,Iz(t)), которые определяются собственными и вынужденными колебаниями ротора Ip(t,Iz(t)) и вынуждающим воздействиям со стороны дефекта Iz(t), может содержать информацию о механических дефектах редуктора [2].
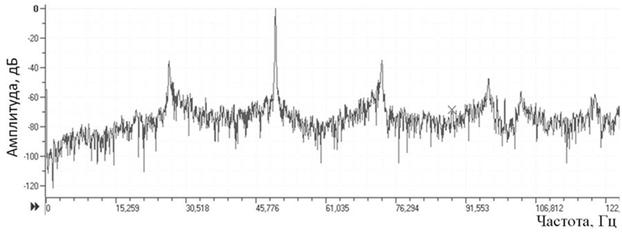
Рис. 2. Спектр сигнала тока двигателя ЭПА с дефектом подшипника редуктора.
Помехи сигнала I(t) затрудняют его анализ. Поэтому в спектре токового сигнала ЭПА (рисунок 2) отсутствуют информативные гармоники, которые обнаруживаются в спектре одновременно снятого виброакустического сигнала (рисунок 1).
Очевидно, сетевая гармоника может быть представлена систематической помехой и подлежит удалению. Штатная методика при обработке диагностических сигналов предполагает вычисление скользящего среднеквадратичного значения (СКЗ) сигнала. В результате усреднения происходит ослабление информативных компонент сигнала.
В ряде работ [1,2,5] в качестве преобразования для демодуляции сигнала, сохраняющей особенности модулирующих сигналов, предлагается фильтр на основе преобразования Гильберта. Преобразование Гильберта функции I(t) позволяет получить мнимую составляющую комплексного представления сигнала:
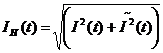 (5)
(5)
При анализе огибающей IH(t) определяются токово-временные параметры (время срабатывания, значение пускового тока, плавность хода и др.). Согласно штатной методике диагностирования, производится сравнение токово-временных параметров арматуры с соответствующими допусками[3]. Несоответствие параметров допускам идентифицируется системой диагностики, как признак неисправности ЭПА. Неравенство (4) соответствует сравнению рабочего тока IH(t) с допусками для данного параметра.
Неравенство выполняется при условии I/p(t,Iz(t))много больше 1. Невыполнение неравенства (4) свидетельствует о пульсации тока двигателя. Причиной пульсаций тока двигателя ЭПА, согласно опыту эксплуатации, являются колебания ротора при периодическом вынуждающем воздействии (1) или (2).
При анализе вынуждающих воздействий по сигналу IH(t) информацию о рабочем токеI0 можно рассматривать как систематическую помеху. Данную помеху необходимо исключить путем вычитания медианного среднего значения Ме:
I/p(t,Iz(t))= IH(t)- Ме (7)
СигналI/p(t,Iz(t)) при разложении в ряд Фурье можно представить суммой периодических функций (8):
![]() (8)
(8)
По спектрам (рисунки 1 и 3) можно видеть, что амплитуды частот ротора больше частот подшипника, то есть диагностический сигнал в значительной степени определяется гармониками, кратными частоте вращения ротора![]() (9)
(9)
Здесь N – число гармоник на частоте вращения ротора. Параметры Iрn, φрn, характеризующие гармоники статора, наведенные в результате вибраций ротора, вообще говоря, не постоянны. Определение динамики данных величин позволяет соотнести сигнал (8) с представлением (1) или (2), т.е. различить крутильные и поперечные колебания. Данная информация позволяет идентифицировать техническое состояние ЭПА в случаях, когда различные дефекты проявляются на одинаковых частотах.
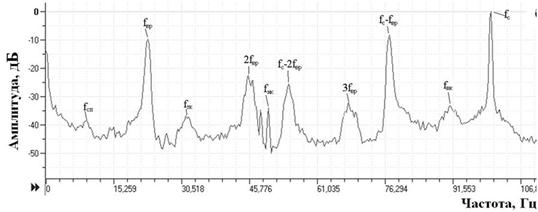
Рис. 3. Спектр сигнала тока двигателя ЭПА с дефектом подшипника редуктора после обработки.
Однако спектральный анализ, основанный представлении сигнала (8) в виде графиков bk(k) или φk(k), не предназначен для выявления данных особенностей. Получить комплексное представление сигнала (8) bk(k,φk) возможно с помощью фазового плоскостного метода (ФПМ)[6]. ФПМ позволяет находить графическое решение уравнений, в том числе уравнений (1) и (2).
Метод предполагает представление диагностического сигнала на комплексной плоскости в виде суммы проекций действительной части сигнала Ir и мнимой H(Ir). Конец результирующего вектора описывает совокупность траекторий, называемых фазовыми портретами (ФП). Формы ФП, соответствующих диагностическим сигналам ЭПА, близки к классу кривых, называемых эпициклоидами[7]. Данные кривые получаются как траектории движения точек, закрепленных на окружностях, катящихся внешним образом по другим окружностям. Вид фигуры зависит от соотношений радиусов окружностей и скоростей качения.
Формы портретов диагностических сигналов определяются соотношением величин, входящих в выражение (9). Если N=1, то портрет представляет собой окружность (рис. 4 а), если N=2, то кардиоиду (рис. 4 б), N=3 – нефроиду (рис. 4 в). При чем, соотношение между диаметрами «лепестков» характеризует соотношения между амплитудами гармоник k=Ip1: (Ip2+Ip3).
Поворот оси симметрии кардиоиды или нефроиды характеризует сдвиг фаз между гармониками φрn. Значение сдвига следует отсчитывать в положительную сторону от оси ординат. Определение данного параметра по спектру затруднительно, поскольку требует подстройки параметров спектра в каждом отдельном случае.
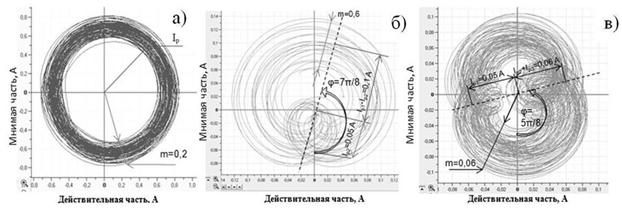
Рис. 4 Фазовые портреты сигналов тока двигателя ЭПА: а - без существенных дефектов; б – с дефектом зубчатой передачи редуктора; в – с дефектом редуктора двигателя.
Флуктуация амплитуд Ipn выражается в спиралеобразном характере очерчивающих линий. Возможна оценка коэффициента амплитудной модуляции m по толщине контура ФП. Отметим, что по ФП оценку коэффициента амплитудной модуляции производить проще, чем по спектру сигнала, поскольку возможна одновременная оценка модуляции всех тональностей и всех гармоник.
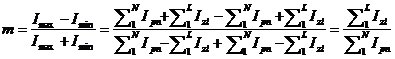
Если разности фаз φрn между гармониками на частоте ротора определяются фазовой модуляцией, то формы ФП соответствуют полярным розам [7](рисунок 5 а). Таким образом, различие амплитудной и амплитудно-фазовой модуляции по ФП очевидно. По виду спектра отличить фазовую модуляцию от многотональной амплитудной затруднительно.
В некоторых случаях (множественные дефекты ЭПА) при наличии выраженной амплитудной и фазовой модуляции на различных частотах можно наблюдать гибридные формы ФП (рисунок 5 б).
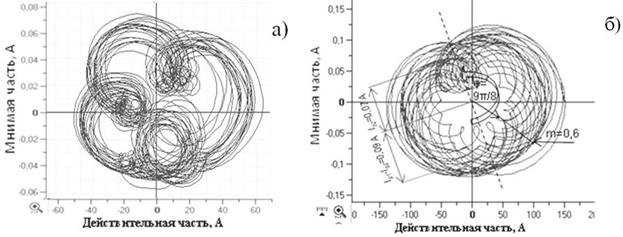
Рис. 5. Фазовые портреты сигналов тока двигателя ЭПА: а - с несоосностью валов редуктора; б – со множественными дефектами редуктора.
Итогом настоящей работы является представленная в Таблице методика, предполагающая поэтапную обработку сигнала с получением информационного комплекса на каждом этапе обработки.
Таблица. Обработка сигналов тока, потребляемого двигателем ЭПА
Этап обра-ботки |
Состав сигнала |
Обработка сигнала |
Информативность |
|
1 |
Сетевая составляющая, типовые характеристики, взаимодействие кинематических пар механизма, колебания ротора, шум. |
Демодуляция (фильтр Гильберта) |
Соответствие типовых характеристик уставкам |
|
2 |
Типовые характеристики, взаимодействие кинематических пар механизма, колебания ротора, шум. |
Выделение участка рабочего хода, централизация, Фурье-преобразование |
Частоты взаимодействия кинематических пар механизма. |
|
3 |
Взаимодействие кинематических пар механизма, колебания ротора, шум. |
Комплексное представление сигнала |
Особенности колебаний ротора |
Данная методика была опробована при диагностике ЭПА как в лабораторных, так и в промышленных условиях. На основании проведенных испытаний можно заключить, что предлагаемые авторами методы обработки диагностической информации позволяют более точно установить состояние диагностируемого оборудования, чем применяемые в данной области штатные методы.
Литература:
- 1.Методы автоматизированного исследования вибрации машин: справочник/ Добрынин С.А., Фельдман М.С., Фирсов Г.И. – М.: Машиностроение, 1987. – 224 с. с ил. – (Основы проектирования машин).
2.Барков А.В., Баркова Н.А., Азовцев А.Ю. Мониторинг и диагностика роторных машин по вибрации: СПб.: Изд.центр СПбГМТУ, 2000, 169 с.
3.Методика оценки технического состояния электроприводной арматуры РЦ и ТЦ энергоблока №1 по ее электрическим параметра. ЭМТД 66-019–06 ПМ, Никифоров В.Н., Пугачева О.Ю., Сиротин Д.В. 2006.
4.Пугачёв А.К., Пугачёва Е.А., Пугачёва О.Ю. «Моделирование дефектов электоприводной арматуры». Известия высших учебных заведений. Северо-Кавказский регион. Технические науки. Состояние и перспективы строительства и безопасной эксплуатации Волгодонской АЭС. Волгодонск 2007.
5.Гадзиковский В.И. Теоретические основы цифровой обработки сигналов. - М.: Радио и связь, 2004. 344 с.
6.Нафиков А.Ф., Закирничная М.М., Сабуров В.К. Использование теории детерминированного хаоса для диагностики роторного оборудования // 55-я научно-техническая конференция студентов, аспирантов и молодых ученых УГНТУ: Сб. тез. докл.– Уфа: УГНТУ, 2004. 218-219 c.
7. Яглом И.М. Комплексные числа и их применение в геомертии. - М.: Физматгиз, 1963 г., 192 с. с ил.