Параметрический метод измерения разности фаз квазигармоничиских сигналов
Аннотация
Дата поступления статьи: 05.07.2013Предложен цифровой параметрический метод измерения фазового сдвига сигналов с медленно меняющимися амплитудами одинаковыми медленно меняющимися мгновенными частотами. Проведено численное моделирование и эксперименты на разработанном аппаратно-программном комплексе. Погрешность измерения разности фаз гармонических сигналов в экспериментах составили не более 0,00001 рад. Метод может быть использован в задачах, где измеряемая величина выражена через разность фаз квазигармонических сигналов.
Ключевые слова: фазовый сдвиг, квазигармонический сигнал, измерения в реальном времени, аппаратно-программный комплекс
05.13.05 - Элементы и устройства вычислительной техники и систем управления
Необходимость точного измерения фазового сдвига возникает при решении задач радиолокации и радионавигации, неразрушающем контроле, радиофизике, радиоастрономии и во многих других прикладных областях [1 – 3]. Прецизионные фазометры используются в радиодальномерах и измерителях геометрических параметров объектов, а также в фазированных антенных решетках [4], однако измерение разности фаз с высокой точностью стандартными методами требует очень большого отношения сигнал/шум. Для повышения точности измерений разности фаз необходимо использовать дополнительную априорную информацию об исследуемых сигналах, а реализация фазометра в виде прибора, работающего в режиме реального времени, возможна только на основе современных цифровых параметрических методов.
Существующие методы измерения разности фаз – метод компенсации фазы, метод преобразования временного интервала в напряжение [1], метод с преобразованием частоты [1, 5], метод на основе преобразовании Фурье [5 – 8], цифровой метод подсчета импульсов [5, 8], ряд корреляционных методов [1, 5] предполагают постоянство частоты и огибающей сигналов на интервале измерения, а точность этих методов сильно зависит от уровня аддитивного шума. Предлагаемый метод может применяться для обработки зашумленных сигналов с существенно изменяющимися на интервале измерения параметрами.
Рассмотрим два гармонических сигнала с одинаковыми частотами, разными фазами и различными огибающими [9]:
![]()
и предположим, что параметры этих сигналов меняются медленно:
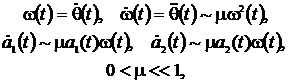
где a(t) – огибающая, ω(t) = ![]() – мгновенная частота.
– мгновенная частота.
Пусть D – некоторый временной интервал, такой, что w(t)D < π/2. При дискретизации сигнала с шагом Dt интервал D может содержать несколько интервалов Dt, то есть D = QDt. Возьмем значения сигналов в точках (t – iD), (i = 0, ..., 4) и разложим их в ряд около центральной точки (t – 2D) с шагом D и 2D:
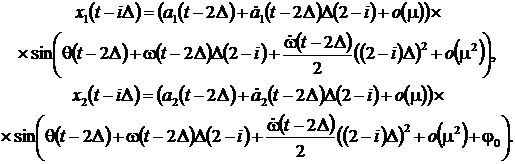
Для простоты введем обозначения:
a1(t – 2Δ) = a1, a2(t – 2Δ) = a2, θ(t – 2Δ) = θ, ω(t –2Δ) = ω.
Рассмотрим две комбинации отсчетов сигнала:
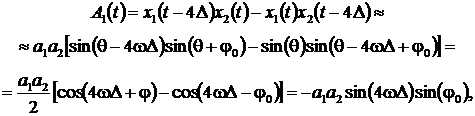 (1)
(1)
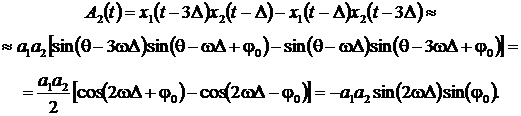 (2)
(2)
Отношение этих величин дает выражение для оценки частоты
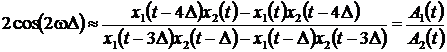 , (3)
, (3)
которая соответствует моменту времени (t – 2D).
Аналогично соотношениям (1) и (2), построим еще две функции
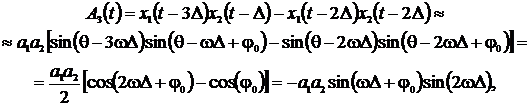 (4)
(4)
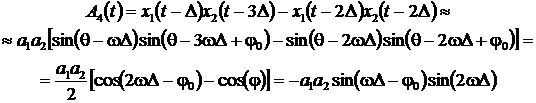 (5)
(5)
и рассмотрим отношение вида
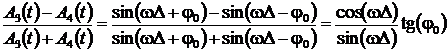 .
.
Отсюда следует выражение для оценки фазового сдвига:
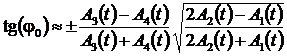 . (6)
. (6)
Перейдем к дискретному времени t = nDt, n = 0,..., N – 1, D = QDt. Тогда соотношения (1), (2), (4) и (5) примут вид
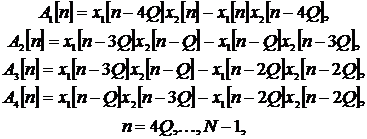 (7)
(7)
а tg(Φ0) может быть найден с помощью метода наименьших квадратов путем минимизации ошибки:
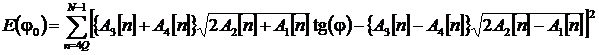 .
.
Выражение для оценки разности фаз примет вид:
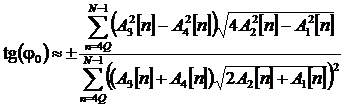 . (8)
. (8)
В этом выражении необходимо использовать знак «+», если сумма в числителе отрицательна, и «–» – если положительна.
Если известно, что частота сигналов на всем временном интервале [0, NDt] постоянна, можно воспользоваться выражением (3), записанным для дискретного времени:
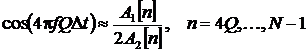 .
.
Применяя метод наименьших квадратов (МНК), получим выражение для оценки частоты:
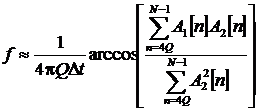 . (9)
. (9)
Для экспериментальной проверки данного метода были разработаны и изготовлены два устройства: двухканальный цифровой генератор (ДЦГ) и блок дискретизации сигналов (БДС) на основе отладочного модуля SK-9G45-OEM [10]. Особенностью ДЦГ является непрерывное генерирование гармонического сигнала с заданной частотой, фазой и модуляцией, причем значение фазы можно задавать не только в начальный момент времени, но и на протяжении генерации всего модельного сигнала. Это позволяет избежать применения управляемых фазовращателей, не обладающих необходимыми метрологическими характеристиками [11]. Структурная схема ДЦГ приведена на рис. 1.
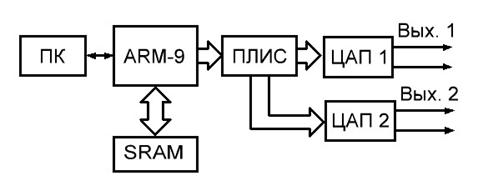
Рис. 1. Структурная схема генератора
Основой устройства является быстродействующий цифро-аналоговый преобразователь (ЦАП) и ARM-процессор AT91SAMG45 [12], работающий на частоте 400 МГц. Благодаря большему объему памяти SRAM, подключенной к процессору, можно создавать непрерывный сигнал, состоящий из более 8 млн. точек разрядностью 16 бит на один канал генератора.
Управление системой производится при помощи персонального компьютера (ПК) c помощью программы, написанной в среде программирования Borland C++ Builder v. 6.0. Программа выполняет несколько задач. В первую очередь настраивается соединение с ДЦГ, подключенным через преобразователь USB-UART, который построен на микросхеме CP2102 [13] и подключен через гальваническую развязку ISO7231 [14] к процессору. Она позволяет избавиться от сетевых наводок ПК, так как питание устройства осуществляется от аккумуляторных батарей. Затем задаются значения амплитуды, частоты и фазы для обоих каналов.
Далее ARM-процессором формируется непрерывная последовательность двух гармонических сигналов с заданными частотами и фазами, которые записываются в память. После окончания записи всей последовательности отсчетов по параллельной шине данных их значения поступают на программируемую логическую интегральную схему (ПЛИС) EPM3256 [15], а затем – на ЦАП. В устройстве используется высокоскоростной двухканальный ЦАП AD9747 [16], что позволяет минимизировать паразитную разность фаз между сигналами. Выходные напряжения генератора лежат в диапазоне, достаточном для наблюдения и оцифровки, поэтому на выходе не требуется устанавливать дополнительные усилители, которые также могут оказаться источниками дополнительной разности фаз.
Структурная схема БДС показана на рис. 2. Он представляет собой отдельное устройство с быстродействующими 16-разрядными аналого-цифровыми преобразователями, ARM-процессором и памятью, в качестве которой применяется SD-карта [17] объемом 2 Гб.
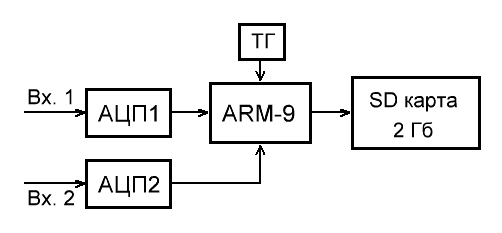
Рис. 2. Структурная схема БДС
Принцип работы устройства заключается в следующем – в первую очередь процессор проверяет наличие внешнего запоминающего устройства (SD), затем формирует на нем файловую систему FAT32 и создает файл для записи информации. Измеряемые сигналы, поступающие на входы АЦП, преобразуются в цифровой код, который затем поступает в память процессора и записывается в файл. Скорость записи на SD-носитель составляет примерно 8 Мб/с.
Измерения производились следующим образом: с помощью ДЦГ создавались два непрерывных гармонических сигнала частотой 104,1 кГц, амплитудой 1 В и заданным фазовым сдвигом между ними φ0. Частота сигналов подбиралась таким образом, чтобы шаг dt между отсчетами ДЦГ превышал шаг дискретизации Dt БДС не менее, чем в 3 раза. При частоте дискретизации, равной 1259,9959 кГц, измеренный сигнал содержал примерно 12 точек на период, а выдаваемый ДЦГ сигнал – 36 точек на период. Для сглаживания генерируемого сигнала к выходу генератора подключался пассивный RC-фильтр, настроенный на четверть частоты дискретизации ДЦГ.
Измерения проводились 30 раз с прерываниями 5 минут после прогрева установки в течение 60 минут. Длина выборки составляла 100000 точек, что соответствует примерно восьми тысячам периодов сигнала.
Предварительная фильтрация сигнала производилась с помощью цифрового полосового фильтра с заданными частотами среза fmin = 103 кГц и fmax = 105 кГц. Импульсная характеристика h[m] КИХ-фильтра с линейной ФЧХ рассчитана методом взвешивания [18] с заданным количеством отсчетов импульсной характеристики M = 1001 и выбранным временным окном w[m] [19]:
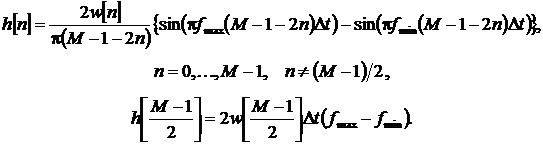
АЧХ такого фильтра считается аналитически:
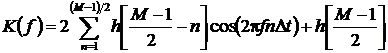 .
.
При исследовании метрологических характеристик разработанного фазометра на первом этапе измерено рассогласование каналов ДЦГ – оба канала формировали гармонические сигналы с одинаковой частотой, фазой и амплитудой. Среднее значение рассогласования <φрас> составило 0,00848224 рад, а среднеквадратичное отклонение (СКО) по 30 реализациям – σрас = 9,23872×10-7 рад. Таким образом, рассогласование каналов практически не меняется, и все дальнейшие результаты были получены с его учетом.
На втором этапе измерялись фиксированные значения фазового сдвига φ0. На рис. 3 показаны зависимости среднего отклонения оценки фазового сдвига <Δφ> и его СКО от задаваемого ДЦГ значения φ0 в пределах от –π/2 до π/2 для гармонических сигналов с частотой 104,1 кГц. Расчет производился по 30 реализациям при N = 100000. Как видно, ошибка отклонения фазового сдвига Δφ растет вблизи значения фазового сдвига –π/2 и π/2, что полностью соответствует результатам численного моделирования.
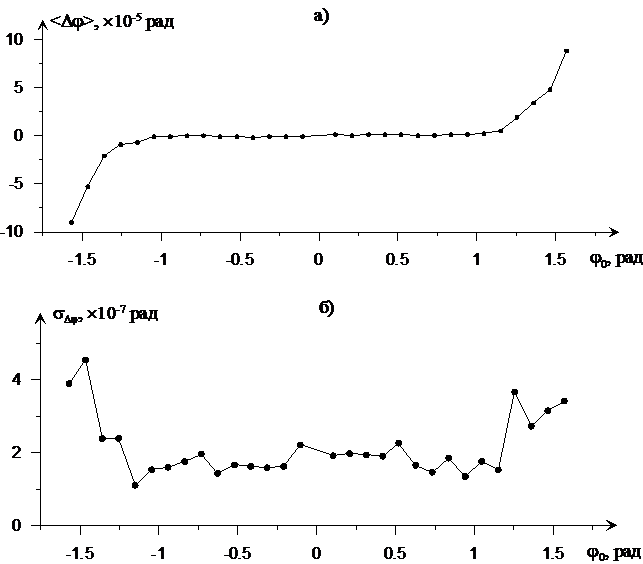
Рис. 3. Зависимость среднего отклонения (а) и СКО (б) оценки фазового сдвига от заданного значения φ0
На рис. 4 показана зависимость СКО оценки разности фаз от длины выборки, рассчитанная по 30 реализациям при заданном значении φ0 = 1. Из графика видно, какое число отсчетов необходимо выбрать для расчета, чтобы получить необходимую точность эксперимента.

Рис. 4. Зависимость СКО оценки разности фаз от длины выборки N
Таким образом, разработанный метод и фазометрическая установка позволяют оценить разность фаз двух сигналов частотой порядка 100 кГц с точностью 10-6 рад в диапазоне от –π/3 до π/3. Если необходимо проводить измерения вне этого диапазона без потери точности, необходимо применять искусственную задержку в одном из каналов, а затем учитывать ее при расчете фазового сдвига. Для этого можно использовать оценку частоты (9) – ее расчет не требует существенного увеличения времени измерения.
Полученные характеристики могут быть улучшены путем увеличения быстродействия и точности АЦП, например – с помощью динамической компенсации погрешностей [20], что позволит довести точность фазометрических систем ориентации до угловой секунды [21].
Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы (соглашения № 14.В37.21.0736 и № 14.В37.21.0284).
Литература:
1. Чмых М.К. Цифровая фазометрия. М.: Радио и связь. 1993. 184 с.
2. Кинкулькин И.Е., Рубцов В.Д., Фабрик М.А. Фазовый метод определения координат. М.: Сов. радио. 1979. 280 с.
3. Манжула В.Г., Крутчинский С.Г., Савенко А.В., Воронин В.В. Интерферометрический интерфейс системы определения относительных координат радиоизлучающих объектов // Инженерный вестник Дона [Электронный ресурс]. 2012. № 3. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2012/1027.
4. Сабиров Т.Р. О формировании излучающими элементами АФАР размещаемой на космическом аппарате эллиптической поляризации поля. Инженерный вестник Дона [Электронный ресурс]. 2013. № 2. Режим доступа: http://ivdon.ru/magazine/archive/n3y2013/1612.
5. Webster J. G. (Ed.) Electrical Measurement, Signal Processing, and Displays. Boca Raton – London – New York – Washington D.C.: CRC Press. 2004.
6. Mahmud S. M. High precision phase measurement using reduced sine and cosine tables // IEEE Transactions on instrumentation and measurement. 1990. 39. N 1. P. 56–60.
7. Гоноровский И.С. Радиотехнические цепи и сигналы. М.: Радио и связь. 1986. 512 с.
8. Метрология и радиоизмерения / Под ред. Нефедова В.И. М.: Высшая школа. 2006. 519 с.
9. Игнатьев В.К., Никитин А.В., Бернардо-Сапрыкин В.Х., Орлов А.А. Измерение разности фаз квазигармонических сигналов в реальном времени. Наука и образование [Электронный ресурс]. 2013. № 7. Режим доступа: http://technomag.edu.ru/doc/588392.html
10. Процессорный модуль SK-9G45-OEM. Инструкция пользователя при совместном использовании с платой SK-9G45-MB. [Электронный ресурс]. – Режим доступа: http://www.starterkit.ru/html/doc/Manual_SK-9G45-OEM_1A.pdf.
11. Зеленчук П.А., Евтушенко А.И. Разработка фазовращателей Ka-диапазона на основе гетероструктур MgO-BST с наноразмерными сегнетоэлектрическими пленками. Инженерный вестник Дона [Электронный ресурс]. 2010. № 4. Режим доступа: http://ivdon.ru/magazine/archive/n4y2010/290
12. Техническое описание микросхемы AT91SAMG45. [Электронный ресурс]. – Режим доступа: http://www.atmel.com/Images/doc6481.pdf.
13. Техническое описание микросхемы CP2102. [Электронный ресурс]. – Режим доступа: https://www.silabs.com/Support%20Documents/TechnicalDocs/ cp2102.pdf.
14. Техническое описание микросхемы ISO7230 [Электронный ресурс]. – Режим доступа: http://www.ti.com /lit/ds/symlink/iso7230a.pdf.
15. Техническое описание микросхемы EPM3256. [Электронный ресурс]. – Режим доступа: http://www.datasheetarchive.com/EPM3256-144-7-datasheet.html.
16. Техническое описание микросхемы AD9747. [Электронный ресурс]. – Режим доступа: http://www.analog.com/static/imported-files/data_sheets/AD9741_ 9743_9745_9746_ 9747.pdf.
17. SD/MMC карта памяти и микроконтроллер AVR (часть 3). Система FatFs [Электронный ресурс]. – Режим доступа: http://www.avrlab.com/node/231.
18. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. М.: Мир. 1978. 848 с.
19. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения. М.: Мир. 1990. 584 с.
20. Игнатьев В.К., Никитин А.В., Перченко С.В., Станкевич Д.А. Динамическая компенсация дополнительной погрешности прецизионного АЦП. Инженерный вестник Дона [Электронный ресурс]. 2012. № 2. Режим доступа: http://ivdon.ru/magazine/latest/n2y2012/771.
21. Коноплев Б.Г., Лысенко И.Е., Шерова Е.В. Интегральный сенсор угловых скоростей и линейных ускорений Инженерный вестник Дона [Электронный ресурс]. 2010. № 3. Режим доступа: http://ivdon.ru/magazine/archive/n3y2010/240.