Воздействие сосредоточенного усилия на анизотропную пороупругую плоскость
Аннотация
Дата поступления статьи: 04.09.2013Исследуется задача о динамике анизотропной пороупругой плоскости под действием сосредоточенного усилия в режиме установившихся колебаний. Построено аналитическое решение задачи в виде однократных интегралов по конечному промежутку. Проведены численные эксперименты по построению решений, полученные результаты сравнены с известными классическими решениями.
Ключевые слова: пороупругость, колебания, анизотропия
Введение
Исследованию пороупругих сред сегодня посвящено множество работ. Данный факт обусловлен тем, что большое число как природных, так и синтетических сред содержат в своей структуре поры, наличие же заполняющей эти поры жидкости вносит значительные поправки в поведение таких сред. Основной моделью для описания движения пороупругого тела является модель Био [1]. Исследованию динамики анизотропной пористой среды посвящена работа [2]. На сегодняшний день учет пористости составляющих задачи можно встретить в различных областях науки так, например, в работе [3] исследуется структура пористого заполнителя в составе бетона, исследованию нефтегазонасыщенного грунта посвящена работа [4], различные труды посвящены аспектам пороупругости в строительстве [5,6]. В представляемой работе речь идет о динамике пороупругой анизотропной плоскости под действием сосредоточенного усилия. Подходы, применяемы при построении решений аналогичны подходам, использованным в задачах термоэлектроупругости [7]
Постановка задачи
Рассмотрим установившиеся колебания трансверсально-изотропной пороупругой плоскости, возбуждаемые сосредоточенным усилием в точке ![]() . Для описания движения такой среды будем использовать модель движения пороупругого континуума, описываемого уравнениями Био [8]:
. Для описания движения такой среды будем использовать модель движения пороупругого континуума, описываемого уравнениями Био [8]:
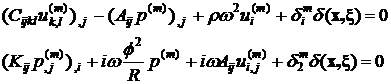
где ![]() -компоненты тензора модулей упругости,
-компоненты тензора модулей упругости, ![]() -компоненты тензора Био,
-компоненты тензора Био, ![]() - компоненты тензора проницаемости среды,
- компоненты тензора проницаемости среды, ![]() -плотность среды,
-плотность среды, ![]() -частота колебаний среды,
-частота колебаний среды, ![]() -компоненты вектора смещений среды,
-компоненты вектора смещений среды, ![]() -давление жидкости в порах,
-давление жидкости в порах, ![]() -пористость среды,
-пористость среды, ![]() -гидростатическая константа,
-гидростатическая константа, ![]() -символ Кронеккера,
-символ Кронеккера, ![]() -дельта функция Дирака, индекс
-дельта функция Дирака, индекс ![]() соответствует наличию слагаемого от действия сосредоточенной нагрузки в соответствующем уравнении.
соответствует наличию слагаемого от действия сосредоточенной нагрузки в соответствующем уравнении.
Построение решения
Применяя интегральное преобразование Фурье по обеим координатам получим систему линейных алгебраических уравнений, решение которой можно представить в виде:
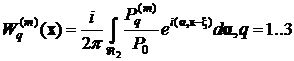
где ![]() - определитель матрицы системы ЛАУ,
- определитель матрицы системы ЛАУ, ![]() - определители матриц, полученных заменой соответствующего столбца основной матрицы на столбец правой части.
- определители матриц, полученных заменой соответствующего столбца основной матрицы на столбец правой части.
После перехода в полярную систему координат путем введения замен ![]() , решение (2) можно представить в виде:
, решение (2) можно представить в виде:
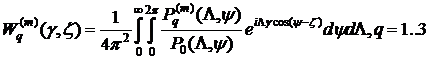
Представим подынтегральную функцию в виде разложения на простейшие дроби: 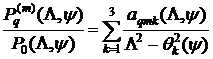 , где
, где ![]() - корни полинома
- корни полинома ![]() . Тогда с учетом периодичности тригонометрических функций, входящих в решение, выражение (3) представимо в виде:
. Тогда с учетом периодичности тригонометрических функций, входящих в решение, выражение (3) представимо в виде:
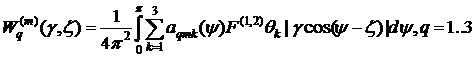
Функции ![]() имеют вид:
имеют вид:
- В случае, когда полином
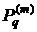 четной степени по
четной степени по 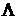 :
:
![]()
- В случае, когда полином
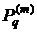 нечетной степени по
нечетной степени по 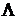 :
:
![]()
Где ![]() - интегральные синус и косинус соответственно.
- интегральные синус и косинус соответственно.
Таким образом решения задачи получены в виде однократных интегралов по конечному промежутку. Численное вычисление таких интегралов можно произвести при помощи различных квадратурных формул, например формулы Гаусса.
Сравним решение поставленной задачи с известным решением для упругой изотропной плоскости, задав изотропный материал и устремив параемтр Био к нулю, что соответствует развязанной задаче.
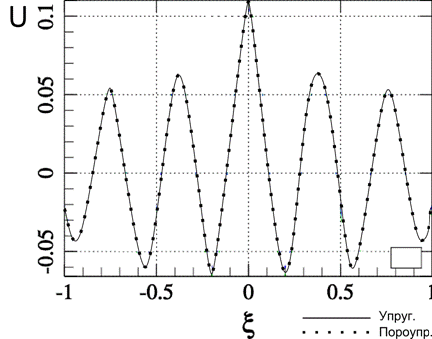
Рис. 1 – Функция смещений ![]() , модуль Био равен нулю.
, модуль Био равен нулю.
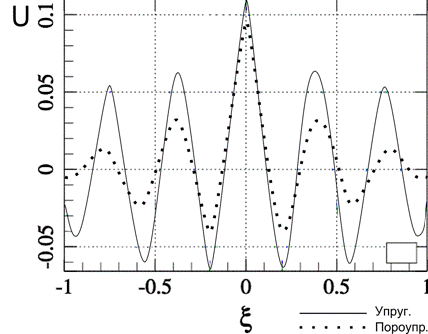
Рис. 2 – Функция смещений ![]() , модуль Био равен 0.6
, модуль Био равен 0.6
Как можно видеть из рис. 1 и рис. 2, наличие в среде жидкой фракции вносит значитльные изменения в характер динамического поведения. Полученные решения можно в дальнейшем использовать в методе граничных интегральных уравнений [9] и методе граничного элемента [10] для исследования задач с объектами произвольного контура или же содержащих в совей структуре полость либо неоднородность.
Работа выполнена при поддержке ФЦП "Научные и научно-педагогические кадры инновационной России" на 2009 – 2013 годы (госконтракты № 14.132.21.1360, 14.132.21.1358).
Литература:
- Biot M.A. Theory of propogation of elastic waves in a fluid-saturated porous solid // Journal of the Acoustical Society of America, - 1956. - V. 28. - № 2. - P. 168-178.
- Carcione J. M. Wave propagation in anisotropic, saturated porous media: Plane wave theory and numerical simulation // Journal of the Acoustical Society of America, - 1996, - № 99, - P. 2655–2666.
- Бычков М. В., Удодов С. А. Особенности разработки легких самоуплотняющихся бетонов на пористых заполнителях [Электронный ресурс] // «Инженерный вестник Дона», 2013, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2013/1774 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Гачаев А.М. О фрактальной структуре нефтегазовых месторождений заполнителях [Электронный ресурс] // «Инженерный вестник Дона», 2011, №1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2011/392 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Аменицкий А.В., Белов А.А., Игумнов Л.А., Гранично-элементный анализ динамической осадки пороупругой колонны // Проблемы прочности и пластичности. 2010 г.. № 72. С. 154-158
- Козин С.В., Ляпин А.А., Об идентификации характеристик неоднородной пороупругой колонны // Современные проблемы механики сплошной среды. Труды XVI международной конференции, г. Ростов-на-Дону, 2012 г., Ростов н/Д: Изд-во ЮФУ., 2012 г. С.134-136.
- Ватульян А.О., Кирютенко А.Ю., Наседкин А.В. Плоские волны и фундаментальные решения в линейной термоэлектроупругости // Прикладная механика и техническая физика, 1996 г. Т.37. № 5, С. 135-142.
- Маслов, Л.Б. Математическое моделирование колебаний пороупругих систем: монография / Л.Б. Маслов. - Иваново: ПресСто, 2010. – 264с.
- Аменицкий А.В., Белов А.А., Игумнов Л.А., Карелин И.С., Гранчиные интегральные уравнения для решения задач трехмерной теории пороупругости // Проблемы прочности и пластичности. 2009 г. № 71. С. 164-171
- Бенерджи, П., Батерфилд, Р. Метод граничных элементов в прикладных задачах / П. Бенерджи, Р. Батерфилд. - Мир, 1984, - 494с.