Развитие инструментария когнитивного моделирования для исследования сложных систем
Аннотация
Дата поступления статьи: 04.09.2013В статье описывается подход к моделированию и анализу функционирования сложных систем основанный на нечетких когнитивных картах. Предложена модель нечеткого импульсного процесса, основанная на нечетком пути. Приводятся описания решений отдельных задач когнитивного моделирования, выполненные с помощью инструментария нечетких орграфов 1-го рода.
Ключевые слова: сложная система, нечеткая модель, нечеткая когнитивная карта, нечеткий путь
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Введение
В последнее десятилетие ученые рассматривают проблему разработки методологии моделирования и исследования функционирования сложных систем с учетом развития новых информационных технологий. К классу таких систем, можно отнести социально-экономические системы (СЭС), геополитические и геоинформационные системы, автоматизированные производственные комплексы и т.д. При моделировании таких систем важнейшей проблемой является знание количественных и качественных закономерностей, присущих данным системам. Одной из важнейших особенностей слабоструктурированных систем является то, что их модель может быть построена только на основании дополнительной информации, получаемой от человека, участвующего в решении проблемы. При этом исчезает почва для построения беспристрастных объективных моделей. Непонимание этого обстоятельства явилось причиной неудач в применении многих "объективных" математических моделей. Классические методы прикладной математики не всегда пригодны для моделирования сложных систем, сегодня популярным становится использовать комплексы, например: теорию нечетких игр, нечеткие множества и логику, знаковые модели в рамках иерархических систем.
Теоретическая часть
На наш взгляд именно предлагаемый в данной статье подход позволит построить модель, которая объединит подсистемы различных показателей как по объекту исследования, так и по своей природе и позволит строить прогноз развития системы, как количественный, так и качественный.
Выбирая базовый аппарат для построения модели сложной системы, на примере СЭС, мы остановились на когнитивном подходе. Опишем семейство нечетких познавательных моделей, кратко их охарактеризуем и проанализируем.
Традиционное понятие когнитивной модели - Cognitive Maps (CM) введено и развивалось в виде знаковых ориентированных графов в работах Р. Аксельрода [1], прикладной характер подробно изложен в известном труде Робертса [2], в котором особое внимание уделяется описанию импульсных процессов для прогнозирования развития ситуаций по орграфу. Однако применять такие модели в сложных системах затруднительно в связи с требованием соответствия используемой информации теоремам об устойчивости.
Следующим шагом в развитии явились результаты научных изысканий Бартоломея Коско. Была исследована взаимосвязь нечеткой логики и теории нейронных сетей и доказана основополагающая FAT-теорема (Fuzzy Approximation Theorem), подтвердившая полноту нечеткой логики [3]. В своей знаменитой теореме Коско доказал, что любая математическая система может быть аппроксимирована системой, основанной на «нечеткой логике».
И наконец, в 80-х годах XX в. увидели свет изобретенные Б. Коско Fuzzy Cognitive Maps (FCMs) − нечеткие когнитивные карты (или модели), на которых базируется большинство современных систем динамического моделирования, в которых причинные связи (связи взаимовлияния), отражают «силу» влияния одного концепта на другой, и могут принимать значения из диапазона от 0 до 1, либо от –1 до +1. В настоящее время FCMs − это теоретическая основа описания поведения любых сложных систем в сфере: финансовые и политические анализы и прогнозы; социальные, биологические и экологические задачи; принятие стратегических решений на основе когнитивных карт и на нечетких моделях в четкой и нечеткой обстановке; ситуационное моделирование мировой политики и т.д.
На сегодняшний день семейство FCMs расширилось, опишем его, выделив основные классы.
Нечеткие когнитивные карты В. Силова [4], в них отношения между концептами рассматриваются как элементы нечеткой матрицы смежности для графа. А проблема обработки отрицательных влияний решается за счет удвоения мощности множества концептов и раздельной обработки положительных и отрицательных влияний.
Нечеткие продукционные когнитивные карты (Rules Based Fuzzy Cognitive Maps, RBFCMs) – это FCMs, основанные на правилах [5], для описания влияний между концептами используются нечеткие продукционные правила.
Обобщенные нечеткие продукционные когнитивные карты (Generalized Rules Based Fuzzy Cognitive Maps, BFCMs) [6], обобщают свойства нечетких продукционных когнитивных карт и реализуют расширенные возможности по анализу и моделированию сложных систем.
Нечеткие реляционные когнитивные карты (Relational Fuzzy Cognitive Maps, RFCMs) и FRM - Fuzzy Relational Maps [7], обеспечивают гибкость построения и анализа нечетких моделей слабоформализуемых систем и проблем за счет реляционного представления нечетких соотношений влияния между концептами.
Нейтрософские реляционные карты (NRMs - Neutrosophic Relational Maps) [8] в их основе которых лежит идея тройственности. Нейтрософской логика характеризует каждое логическое утверждение в 3D-нейтрософском пространстве, где каждое измерение пространства представляет соответственно истину (T), ложь (F) и неопределенность (I) рассматриваемого утверждения, а T, F, I соответственно являются стандартными или нестандартными вещественными подмножествами ![]() .
.
Динамические когнитивные сети (DCNs) [9] используют аппарат дифференциальных уравнений для описания модели.
Более подробный анализ и развитие DCNs в сторону нечетких нейронных сетей проведен в [10], где авторами предложена классификация способов интеграции нечетких и нейронных сетей.
FCMs, основанные на нечетких реляционных уравнениях описываются в [11], в частности предлагается решение задачи подстройки весов FCMs с помощью параллельной реализации генетического алгоритма обучения модели когнитивной карты, основанной на нейронной модели.
Когнитивные карты (СМ), нечеткие когнитивные карты (FCMs), и динамические когнитивные сети (DCNs) являются комплексным инструментарием, позволяющим моделировать познание людей и строить машинные выводы. FCMs расширяют СМ, а динамические в свою очередь, расширяют FCMs. Недостатком DCNs является высокая сложность, а CMs/FCMs не достаточно адекватно отображают объект исследования. В работе [12] описывается упрощенная распределенная вычислительная сеть (sDCN), которая расширяет возможность моделирования FCMs/CM, при этом сохраняя относительную простоту. В статье доказывается, что существует теоретическая эквивалентность среди моделей в семье когнитивных карт СМ, FCMs, и sDCNs. Например, каждому sDCN, может соответствовать FCMs или СМ, и наоборот; точно так же каждая FCMs может быть представлена СМ, и наоборот. Т.о. СМ, FCMs, и sDCNs – это семейство познавательных моделей, которое отличается от многих расширенных моделей. Известен конструктивный подход к преобразованию одной модели CM в другие модели семейства.
Описание инструментария
Подчеркивая плюсы и минусы вышеописанных моделей, мы остановились на идее, заложенной в FCMs Б. Коско, но предлагаем развитие аппарата построения когнитивных карт в виде нечетких ориентированных графов 1-го и 2-го рода.
Нечеткие модели оперируют такими понятиями, как нечеткая переменная, нечеткое множество, лингвистическая переменная. Как известно нечетким множеством А на множестве Х называется совокупность пар вида ![]() , где
, где ![]() – функция принадлежности, принимающая значения в интервале [0, 1], т.е.
– функция принадлежности, принимающая значения в интервале [0, 1], т.е. ![]() . Когда Х непрерывно, то нечеткое множество А может быть кратко описано как
. Когда Х непрерывно, то нечеткое множество А может быть кратко описано как ![]() . В случае дискретного Х, нечеткое множество А представляется как
. В случае дискретного Х, нечеткое множество А представляется как 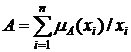 .
.
Введем понятие, FCMs –это нечеткий ориентированный граф (орграф) первого и/или второго рода. Нечетким ориентированным графом первого рода называется и через ![]() обозначается пара множеств, у которого
обозначается пара множеств, у которого ![]() – четкое множество вершин (или концептов), а
– четкое множество вершин (или концептов), а ![]() – это нечеткое множество ребер (или дуг), где
– это нечеткое множество ребер (или дуг), где ![]() , а
, а ![]() − это степень принадлежности ориентированного ребра
− это степень принадлежности ориентированного ребра ![]() нечеткому множеству ориентированных ребер
нечеткому множеству ориентированных ребер ![]() . Нечетким ориентированным графом второго рода называется граф
. Нечетким ориентированным графом второго рода называется граф ![]() , где
, где ![]() − множество вершин (или концептов) является нечетким множеством в некотором универсальном множестве A, т.е.
− множество вершин (или концептов) является нечетким множеством в некотором универсальном множестве A, т.е. ![]() ,
, ![]() − нечеткое множество ориентированных ребер (или дуг) определяется как
− нечеткое множество ориентированных ребер (или дуг) определяется как ![]() ,
, ![]() , где X – носитель нечеткого множества
, где X – носитель нечеткого множества ![]() [13].
[13].
Отметим, что нечеткий ориентированный граф 2-го рода при необходимости можно однозначно преобразовать в нечеткий ориентированный граф 1-го рода , как и наоборот, в последнем случае мы получим бесконечно много нечетких графов второго рода, что не оптимально.
Нечеткий орграф первого рода удобно задавать в виде ![]() , где
, где ![]() , а
, а ![]() - нечеткое многозначное отображение множества вершин X в себя, т.е.
- нечеткое многозначное отображение множества вершин X в себя, т.е. ![]() , задаваемое в виде системы нечетких образов элементов
, задаваемое в виде системы нечетких образов элементов ![]() при этом отображении, т.е.
при этом отображении, т.е. ![]() , здесь
, здесь ![]() – четкое множество образов вершины
– четкое множество образов вершины ![]() .
.
Нечеткий ориентированный путь из вершины xi в вершину xm есть ![]() и это направленная последовательность нечетких дуг, ведущая из вершины xi в вершину xm, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей дуги:
и это направленная последовательность нечетких дуг, ведущая из вершины xi в вершину xm, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей дуги:
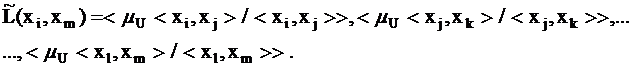 (1).
(1).
Для пути ![]() определим его конъюнктивную прочность следующим образом:
определим его конъюнктивную прочность следующим образом: ![]() [14].
[14].
В приведенных выше выражениях операции конъюнкции − & и дизъюнкции − v могут интерпретироваться в различных нечетких базисах, в дальнейшем будем под этими операциями подразумевать операции минимума и максимума соответственно.
Путем с минимальной прочностью ![]() будем называть ориентированный нечеткий путь между вершинами xi и xm, для которого величина
будем называть ориентированный нечеткий путь между вершинами xi и xm, для которого величина ![]() минимальна. Естественно, что аналогичные определения могут быть даны с использованием выражений
минимальна. Естественно, что аналогичные определения могут быть даны с использованием выражений ![]() ,
, ![]() и для нахождения путей с максимальной прочностью.
и для нахождения путей с максимальной прочностью.
Из вышеизложенного и предметных областей, которые представляются нечеткими ориентированными графами 1-го и 2-го рода, ясно, что при определении путей и их прочностей возможны самые различные комбинации нечетких операций и их интерпретаций в различных нечетких базисах. Предлагается в дальнейшем использовать минимаксный базис и конъюнктивную прочность пути, которую будем обозначать ![]() .
.
Моделирование на графовой модели проводится шагами, которые называют импульсами или элементарными возмущениями. Суть этого процесса заключается в следующем: одной из вершин задается возмущение, которое влечет за собой изменение показателей на всех остальных вершинах по цепочке, причем усиливаясь или затухая. Значения в вершинах будут меняться через каждый шаг имитации t. Подробно этот подход с иллюстративным примером изложен в [15].
Обозначая вершины орграфа совокупностью u1, u2, ..., un, введем обозначения: ![]() − вектор исходных значений вершин;
− вектор исходных значений вершин; ![]() − вектор начальных импульсов;
− вектор начальных импульсов; ![]() − вектор значений вершин в момент времени t, тогда:
− вектор значений вершин в момент времени t, тогда: ![]() , где
, где ![]() − вес дуги из вершины uj в вершину ui, принимающий значения -1, 0 или +1; pj(t) − изменение в вершине uj в момент времени t. Для модели CM известна следующая формула развития импульсного процесса:
− вес дуги из вершины uj в вершину ui, принимающий значения -1, 0 или +1; pj(t) − изменение в вершине uj в момент времени t. Для модели CM известна следующая формула развития импульсного процесса: ![]() .
.
Для модели FCMs данный подход не работоспособен в виду природы нечеткого графа. Предлагается следующая интерпретация импульсного моделирования, вместо четких весов ![]() вводим в формулу нечеткий путь
вводим в формулу нечеткий путь ![]() , описанный моделью (1), тогда:
, описанный моделью (1), тогда:
![]() (2)
(2)
Применение инструментария для решения задач
На сегодняшний день сложился стандартный перечень задач когнитивного моделирования, некоторые из них решены предложенным подходом.
В [14] описаны следующие задачи: анализ путей и циклов; определение путей и их прочности между концептами FCMs; анализ связности и сложности системы; определение степени связности графа.
В работе [13] адаптирован метод анализа нечеткой базы и антибазы к решению задачи установления похожести (аналогии) социально-экономических систем, моделируемых различными нечеткими графами.
В работе [16] предложен подход, использующий нечеткие множества для моделирования силы управляющего воздействия при разных типах связей между предшествующей и последующей целями функционирования на различных слоях FCMs.
Как известно выбор управленческого решения в сложной системе с помощью метода анализа иерархий всегда сопровождается неопределенностью, которая в свою очередь может быть выражена в следующем виде:
1) точечные оценки с функциями распределения вероятностей,
2) интервальные оценки без вероятностного распределения,
3) нечеткие оценки в виде нечетких чисел
Один из видов нечеткости в графах как раз и предполагает, что вес над дугой определяется функцией принадлежности. Но в этом случае мы имеем, хоть и множество значений с достаточно большой степенью детализации, но все же единственное число, что возвращает нас к четким CM. Поэтому в качестве веса над дугой и более того, степени значимости вершины предлагается использовать нечеткие интервалы.
Для поиска решений в нечеткой иерархической системе управления, где отдельные вершины представлены нечеткими интервалами с границами на разных шкалах, неприменим подход, основывающийся на определении степени нечеткого равенства нечетких чисел. Поэтому предлагается применять подход, основанный на сравнении нечетких интервалов.
В [17] описывается применение аппарата нечеткой логики и нечетких множеств. Предложен способ нахождения переходов между эталонными ситуациями в многоуровневых сложных системах, основанный на сравнении нечетких интервалов, подробно изложен алгоритм сравнения нечетких множеств на единичном интервале.
В работе [18] используются нечеткие динамические графы для решения задачи нахождения максимального потока минимальной стоимости в нечеткой динамической системе. Особое внимание уделяется учету нечеткого характера основных параметров системы.
В [19] предлагается использование нечетких графов для моделирования и анализа функционирования сложных систем. Рассматриваются вопросы анализа сложной системы как нахождение живучести нечеткого ориентированного графа в случае, когда под живучестью понимается степень его сильной связности.
Заключение
С учетом современных тенденций, рассматривая любую сложную систему необходимо учитывать то, что главным действующим лицом ее является человек, поэтому неточность и субъективность в этой системе присутствует по природе. Вот почему, выбран нечеткий подход в виде FCMs, построенных как нечеткий орграф 1-го рода, к моделированию поведения динамических систем. С помощью предложенной модели (2) возможно построение прогнозных сценариев развития сложной системы, с учетом реакции на внешние воздействия.
Литература:
- Axelrod Robert M. Structure of decision: The Cognitive Maps of Political Elites [Text] / R. Axelrod – Princeton, NJ, Princeton University Press, 1976, 404 p.
- Робертс Ф.С. Дискретные математические модели с приложением к социальным, биологическим и экологическим задачам [Текст] / Ф.С. Робертс – М.: Наука, 1986. – 496 с.
- Kosko B. Fuzzy Thinking: The New Science of Fuzzy Logic [Text] / B. Kosko // Hyperion, Disney Books 1993, − 336 p.
- Силов В.Б. Принятие стратегических решений в нечеткой обстановке [Текст] / В.Б. Силов − М.: ИНПРО-РЕС, 1995. − 228 с.
- Carvalho J.P. Rule-based fuzzy cognitive maps and fuzzy cognitive maps - a comparative study [Text] // In Proceedings of the 18th international conference of the North American fuzzy information, 1999, by NAFIPS, p.115 – 119.
- Федулов А.С., Борисов В.В. Обобщенные нечеткие когнитивные карты [Текст] // Нейрокомпьютеры: разработка, применение. – 2004. – № 4. – С. 3–21.
- Федулов А.С. Нечеткие реляционные когнитивные карты [Текст] // Известия РАН. Теория и системы управления. – 2005. – № 1. – С. 120–133.
- Смарандаке Ф. Сущность нейтрософии [Текст] / Ф. Смарандаке − США, Аризона: HEXIS Publishers, 2006. − 34 с.
- Y. Miao, ChunYan Miao, XueHong Tao, ZhiQi Shen, ZhiQiang Liu. Transformation of cognitive maps [Text] // IEEE Transactions on Fuzzy Systems. Volume 18 Issue 1, February 2010 p.114-124.
- Борисов В.В., Федулов А.С. Способы интеграции нейронных и нечетких сетей [Текст] // Нейрокомпьютеры: разработка, применение. – 2007. – № 1. – С. 5–11.
- Аверкин А.Н., Паринов А.А. Параллельная реализация генетического алгоритма обучения нечетких когнитивных карт [Текст] // Труды 13-ой национальной конференции по искусственному интеллекту с международным участием КИИ-2012: Труды конференции. Т.2.- Белгород: Изд-во БГТУ, 2012. С.323-329.
- Y. Miao, ChunYan Miao, XueHong Tao, ZhiQi Shen, ZhiQiang Liu. Transformation of cognitive maps [Text] // IEEE Transactions on Fuzzy Systems. Volume 18 Issue 1, February 2010 p.114-124.
- Боженюк А.В., Гинис Л.А. Об использовании нечетких баз и антибаз при анализе нечетких когнитивных карт [Текст] − Украина, Донецк, ИПИИ «Наука i освiта», 2004. – №4 – С. 276-285.
- Боженюк А.В., Гинис Л.А. О нахождении нечетких путей и компонент сильной связности между слоями иерархических познавательных карт [Текст]. − Донецк, ИПИИ, «Наука i освiта», 2005г. – №3 – С. 336-347.
- Горелова Г.В., Рябцев В.Н. Когнитивный подход к исследованию геополитических процессов в мировых регионах и когнитивное моделирование их развития (на примере Черноморско-Каспийского региона) [Электронный ресурс] // «Инженерный вестник Дона». – 2012. № 4-2 (Том 23) − Режим доступа: http://ivdon.ru/magazine/archive/n4p2y2012/1407 (доступ свободный) − Загл. с экрана. – Яз. рус.
- Vovk S.P., Ginis L.А. Modelling and forecasting of transitions between levels of hierarchies in Difficult formalized systems [Text] // European Researcher. − 2012, − Vol. (20), − №5-1, − с.541-545.
- Вовк С.П., Гинис Л.А. Моделирование переходов между эталонными ситуациями в сложных системах в условиях неопределенности [Текст] // Известия ЮФУ. Технические науки. − Таганрог: Изд-во ТИ ЮФУ, 2013. №2 (139). – 260 с. С. 116-122.
- Боженюк А.В., Герасименко Е.М. Разработка алгоритма нахождения максимального потока минимальной стоимости в нечеткой динамической транспортной сети [Электронный ресурс] // «Инженерный вестник Дона». – 2013. № 1 (Том 24).. − Режим доступа: http://ivdon.ru/magazine/archive/n1y2013/1583 (доступ свободный) − Загл. с экрана. – Яз. рус.
- Боженюк А.В., Гинис Л.А. Применение нечетких моделей для анализа сложных систем [Текст] // Системы управления и информационные технологии. – Москва – Воронеж: Изд-во «Научная книга», 2013. № 1.1(51). – С.122-126.