Методика определения коэффициента зернограничной диффузии примеси в металлах на основе численного решения по модели Фишера
Аннотация
Дата поступления статьи: 18.10.2013Предлагается методика оценки величины коэффициента зернограничной диффузии атомов примеси в металлах путем построения графика зависимости отношения глубин объемной и зернограничной диффузий от отношения коэффициентов диффузии атомов примеси в них. Для этого используется численное решение диффузионной задачи Фишера, свободное от упрощений в моделировании процесса ЗГ диффузии, что позволяет применять методику в экспериментах с широким варьированием параметров диффузионного отжига. Приведены примеры использования методики для оценки величин коэффициента зернограничной диффузии меди в поликристаллическом никеле и отношения максимальных глубин диффузии серебра в зерне и межзеренной областях в субмикрокристаллической меди.
Ключевые слова: металлы, субмикрокристаллические и наноструктурированные материалы, зернограничная диффузия, коэффициент диффузии
Диффузионные процессы существенным образом определяют эксплуатационные свойства материалов. Особенное влияние имеет зернограничная (ЗГ) диффузия - диффузия в твердых поликристаллических телах, сосредоточенная в узких зонах на границах зерен с различной кристаллографической ориентацией. Благодаря высокой концентрации дефектов на этих границах, диффузионный перенос по ним протекает значительно быстрее, чем в их объемах. Исследования ЗГ диффузии ведутся очень давно [1], но в настоящее время наблюдается новый всплеск интереса по этой тематике. Это обусловлено разработкой и широким внедрением технологий субмикро- и нанокристаллических и наноструктурированных материалов [2,3] с применением различных обработок. Практически все авторы экспериментальных работ отмечают большой разброс не только значений, но и порядков величин коэффициентов ЗГ диффузии атомов примеси в металлах одного типа, но различающихся по структуре (например, поликристаллический и наноструктурированный никель). Причиной разброса наряду с фактором неравновесного состояния границ зерен в таких материалах, в том числе, может быть некорректный выбор способа определения коэффициента ЗГ диффузии.
Общепризнано считается [4-6], что основной моделью процесса зернограничной диффузии, является модель Фишера [1]. В этой модели граница рассматривается в виде однородной изотропной пластины шириной d, расположенной перпендикулярно поверхности, между двумя полубесконечными зернами, коэффициент диффузии атомов в которой D' отличается от коэффициента диффузии в объеме D (рис.1).
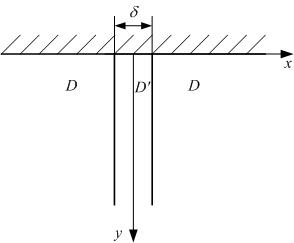
Рис.1. – Модель границы зерен по Фишеру
Математической основой модели процесса диффузии является дифференциальное уравнение, представляющего собой 2-й закон Фика для двумерного случая, с соответствующими начальными и граничными условиями, а также условием баланса вещества в границе. Концентрационный профиль, получаемый в результате решения, имеет вид так называемого «диффузионного клина» [4]. Для экспериментального определения величины D', как правило, используют линейную аппроксимацию концентрации примеси от координаты и определяют тангенс угла ее наклона (в некоторых случаях, непосредственно угол наклона диффузионного клина), величина которого связана с коэффициентом D, временем диффузионного процесса t, и произведением δD' [4,5]. Чтобы обеспечить нормальную точность определения D', необходимы адекватный выбор условий эксперимента и метода математического описания результатов эксперимента по модели Фишера. Последний, как правило, строится на основе аналитического решения диффузионной задачи Фишера с использованием ряда упрощений и допущений, что приводит к классификации режимов ЗГ диффузии [6]. Как минимум, выделяют два параметра λ и β и условия для них:
![]() и
и ![]() (1)
(1)
Как правило, эти условия соответствую низким температурным отжигам в малом диапазоне (Т=0,5Тпл ÷ 0,7Тпл), малым временам диффузии, большим отношениям и узким диффузионным клиньям. В случае если условия эксперимента приводят к искажению экспоненциальной формы диффузионного клина, применение линеаризуемых форм для обработки результатов эксперимента, как отмечают в [4], является “незаконным”. В этом случае необходимо использовать численное решение рассматриваемой задачи.
Выполнение численного решения задачи Фишера, как показано в [7,8], позволяет значительно расширить ее применение для ряда практически важных задач.
В настоящей работе излагается методика оценки величины коэффициента ЗГ диффузии в металлах, которой можно воспользоваться, не заботясь о выполнении условий (1).
Согласно предлагаемой методике для вычисления D' атомов какой-либо примеси в металле необходимо, во-первых: получить информацию о значении коэффициента диффузии атомов этой примеси в объеме зерна при данной температуре. Это можно сделать двумя способами: либо рассчитать по закону Аррениуса, либо определить экспериментально одним из известных способов [9]. Затем из результатов эксперимента диффузионного отжига следует определить глубины максимального проникновения атомов примеси в объем зерна L и межзеренную область L' для одного и того же значения концентрации примеси. Наиболее подходящими в данном случае являются авторадиографические методы и методы электронной микроскопии. Далее, используя численное решение задачи Фишера [8], необходимо провести серию вычислительных экспериментов, целью которых является построение теоретической зависимости отношения глубин от отношений для заданных значений D и t. На установленной зависимости остается отыскать точку, соответствующую экспериментально определенному отношению , и произвести вычисление D'.
Приведем пример расчета по предлагаемой методике. Для этого воспользуемся условиями и результатами эксперимента из работы [10]. На рис. 2 приведены результаты численного расчета по задаче Фишера, представляющие собой линии равной концентрации атомов меди в поликристаллическом никеле с δ = 100Å. Температура диффузии Т = 1073К, время t=5 часов. Для удобства обозначения параметров L и L', приведены графики изоконцентрационных линий, соответствующие значению =10.
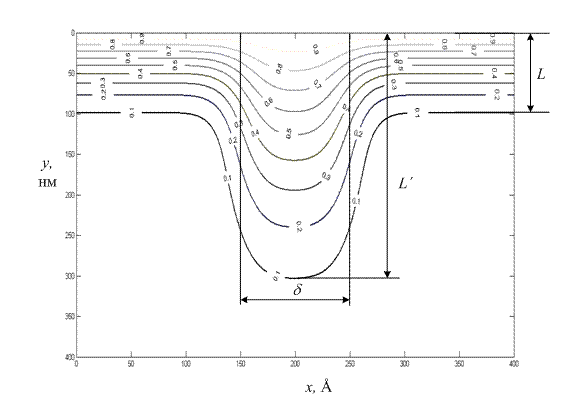
Рис. 2. – Изолинии меди в никеле в процессе ЗГ диффузии
Важно отметить заметное влияние на распределение концентрации атомов примеси так называемой боковой диффузии, которая существенна даже при выбранном времени, но которой зачастую пренебрегают в расчетах D', что является одним из источников погрешности в определении коэффициента ЗГ диффузии.
На рис. 3 прямой сплошной линией изображена рассчитанная зависимость отношения глубин от для изоконцентрационной линии со значением 0,1 (значение коэффициента диффузии меди в объеме зерна поликристаллического никеля при указанной температуре взято из [10] и составляет D=2∙10-17м/с2). На ней отметим точку, соответствующую экспериментальному значению![]() ≈600. Как видно этому отношению удовлетворяет =6∙105, из чего заключаем, что D'=1,2∙10-11м/с2.
≈600. Как видно этому отношению удовлетворяет =6∙105, из чего заключаем, что D'=1,2∙10-11м/с2.
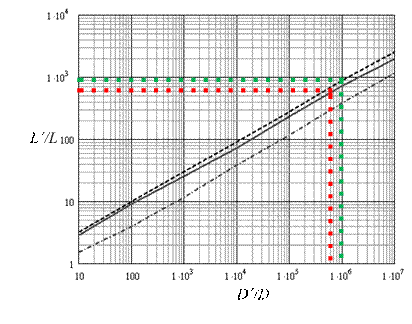
Рис. 3. – Графики для примера расчетов D' и ![]()
Полученное значение совпадает в пределах погрешности вычислений с D', приводимым в работе [11], рассчитанным авторами с использованием метода линейной аппроксимации координатной зависимости концентрации атомов, как было сказано выше, что подтверждает корректность предлагаемой методики. Кроме того, на рис. 3 пунктирной и штрихпунктирной линиями показаны рассчитанные графики зависимостей отношений глубин и коэффициентов диффузии для значений D=2∙10-20м/с2 и D=2∙10-25м/с2 соответственно.
Возможно решение и обратной задачи, когда по известным значениям D, D' можно оценить величину максимальной глубины ускоренной диффузии примеси по границе зерен L' или отношение . Например, теоретический расчет с использованием графика на рис. 3 позволяет утверждать, что при диффузии серебра в сумбмикрокристаллическую медь с размером зерна 300 нм, обработанную воздействием интенсивной пластической деформации, при температуре 423 К, отношении коэффициентов =106 и D = 2∙10-20м/с2 [3] глубина ЗГ диффузии будет в 900 раз превышать объемную. Такое использование численного решения задачи Фишера целесообразно при оптимизации толщин металлических и других покрытий, применяемых, например, в производстве проводов [12] или сенсорной техники [13].
Разработанная методика оценки величины коэффициента ЗГ диффузии примеси в металлах не требует исследования послойной активности или распределения концентрации в границе зерен, как при использовании металлографических методов. Кроме того, расчет D' не сопровождается упрощениями или допущениями в моделировании физического процесса ЗГ диффузии. Таким образом, методику можно рекомендовать для использования в теоретических исследованиях роли примесей в диффузионно-контролируемых процессах в металлах и экспериментах с широким варьированием параметров диффузионного отжига.
Литература:
1. Fisher J.C. Calculation of diffusion penetration curves for surface and grain boundary diffusion // J.Appl. Phys. – 1951. – Vol. 22, no. 1. – P. 7477.
2. О.Е. Положенцев, В.В. Шаповалов и др. Динамика наноразмерной атомной структуры новых наноструктурированных конденсированных материалов для возобновляемых источников тока на основе нанокомпозита V2O5/Fe/LiF в цикле зарядка-разрядка [Электронный ресурс] // «Инженерный вестник Дона», 2012, № 4. Часть 2 – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1465 (доступ свободный) – Загл. с экрана. – Яз. рус.
3. Колобов Ю.Р., Липницкий А.Г. и др. Роль диффузионно-конролируемых процессов в формировании структуры и свойств металлических наноматериалов [Текст] // Композиты и наноструктуры, 2009. – №2. – С. 5–24.
4. Бокштейн Б.С., Копецкий Ч.В., Швиндлерман Л.С. Термодинамика и кинетика границ зерен в металлах [Текст]: Монография / Б.С. Бокштейн. – М.: Металлургия, 1986. – 224 с.
5. Любов, Б.Я. Диффузионные процессы в неоднородных твердых средах [Текст] / Б.Я. Любов. – М.: Наука, 1981. – 296 с.
6. Kaur. I., Mishin Yu., and Gust W. Fundamentals of Grain and Interphase Boundary Diffusion. – Chichester, New York, Toronto: John Wiley & Sons Ltd, 1995. – 512 p.
7. Какурин Ю.Б., Захаров А.Г., Котов В.Н. Моделирование массопереноса в неоднородных полупроводниковых структурах [Текст] // Нано- и микросистемная техника. – 2008. – №6. – С. 22 – 25.
8. Какурин Ю.Б., Захаров А.Г., Филипенко Н.А. Моделирование процессов массопереноса в неоднородных твердых телах с учетом электродиффузии [Текст] // Известия вузов. Северо-Кавказский регион. – 2009. – № 2. – С. 35 –37.
9. Бокштейн Б.С. Диффузия в металлах [Текст]: Монография / Б.С. Бокштейн. – М.: Металлургия, 1978. – 312 с.
10. Миколайчук М.А., Князева А.Г., Грабовецкая Г.П., Мишин И.П. Изучение влияния механических напряжений на диффузию в пластине с покрытием [Текст]. //Вестник ПНИПУ. Механика, 2012. – №3. С. 120 – 134.
11. Сравнительные исследования зернограничной диффузии меди в субмикро-и крупнокристаллическом никеле / Г.П. Грабовецкая, И.В. Раточка и др. // Физика металлов и металловедение. –1997. – Т. 83, № 3. – С. 112–116.
12. Чайко В.Ю. Диффузия в тонких металлических покрытиях на медной проволоке [Текст] //Наука и Техника, 2006. – № 5. С. 3– 9.
13. Моисеева Т.А., Мясоедова Т.Н. и др. Разработка газочувствительного элемента на основе пленок оксидов меди для датчика аммиака [Электронный ресурс] // «Инженерный вестник Дона», 2012, № 4. Часть 1 – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1465 (доступ свободный) – Загл. с экрана. – Яз. рус.