Аппаратно-программный комплекс для параметрического анализа сигналов в задачах технической диагностики
Аннотация
Дата поступления статьи: 20.09.2013В работе описан аппартно-программный комплекс параметрического оценивания сигналов, с его помощью экспериментально удалось достигнуть точности измерения разности фаз между двумя квазигармоническими сигналами на уровне 10 мкрад.
Ключевые слова: параметрический анализ, техническая диагностика, разность фаз
В наиболее общей постановке процесс диагностики может рассматриваться как идентификация нестационарной системы, искомыми параметрами которой являются медленно меняющиеся в пространстве и времени измеряемые физические величины, содержащие максимально возможную информацию о системе [1]. В задачах медицинской и промышленной диагностики целевой эффект операции определяется сочетанием объема полученной информации и временных затрат. Издержки материальных средств, существенные в понятии экономической эффективности, в данном случае малозначимы в сравнении с требованием высокой точности обработки данных в режиме реального времени, поскольку убытки от катастроф из-за неверного или несвоевременного диагноза могут намного превысить стоимость диагностического комплекса [2].
Наиболее информативным методом диагностики в настоящее время является радиоволновое дистанционное зондирование, используемое в задачах аэрокосмического мониторинга атмосферы и геопространственных данных, ЯМР томографии, мониторинге технического состояния зданий и сооружений, неразрушающего контроля и технической диагностики. В рамках этих задач изменение динамических параметров объекта проявляется в изменении частоты, фазы и огибающей излучаемой или отраженной волны [3 – 9]. При этом часть параметров нестационарной системы, например частоты зондирующих сигналов и координаты передатчиков и приемников, могут полагаться известными [10]. Частота гармонического сигнала в настоящее время определяется с наивысшей точностью, поэтому преобразование в частоту обеспечивает максимально достижимую точность измерения контролируемых параметров. Фаза как истинный скаляр является релятивистским инвариантом, фазовые измерения обеспечивают максимальную помехозащищенность и информативность. Огибающая определяет энергию квазигармонического процесса и входит в уравнения движения нестационарной системы как обобщенная координата [11]. Поэтому применение радиоволновых параметрических методов обеспечивает существенное повышение эффективности диагностических комплексов.
Поскольку показатель эффективности обработки сигнала в диагностических комплексах определяется объемом полученной в режиме реального времени информации, требование сохранения общей размерности массивов обрабатываемых данных, ключевое для концепции многоскоростной обработки, следует заменить требованием сохранения объема информации, содержащихся в обрабатываемых данных. Сама концепция многоскоростной обработки при этом переходит в концепцию параметрической обработки, когда выходной поток представляет собой многомерную последовательность медленно меняющихся параметров, дискретизированную с частотой, существенно меньшей частоты дискретизации входного потока, но сохраняющую всю информацию, в нем содержащуюся. При этом входной поток рассматривается как не аддитивная, а мультипликативная композиция быстрых и медленных составляющих, разделение происходит не предварительно, а в ходе обработки, что существенно изменяет алгоритмы этой обработки.
Широкое распространение параметрических методов в настоящее время в первую очередь связано с растущей вычислительной мощности современных процессоров, а также с их невысокой стоимостью. Эти факторы в совокупности с появлением современных высокоскоростных интерфейсов приема-передачи данных, таких как USB 3.0, Thunderbolt, PCI-Express и др., позволяют использовать ПК в технической диагностике, как высокоэффективный инструмент анализа и визуализации диагностической информации.
Разработанный аппаратно-программный комплекс предназначен для анализа разности фаз двух квазигармонических сигналов по методу, описанному в работе [12]. Комплекс состоит из двух прецизионных 16-битных АЦП, микроконтроллера CYUSB3014 [13] и ПК с поддержкой интерфейса USB 3.0. Частота дискретизации сигнала ограничивается только максимальной частотой работы 32-х разрядного порта GPIF II микроконтроллера [13], и при использовании соответствующих АЦП, например LTM9002, может быть увеличена до 100 МГц.
Оценка собственных погрешностей прибора проведена для различных источников входного сигнала и тактирующих сигналов АЦП. В первой серии экспериментов в качестве тактового генератора установки использовался термостатированный кварцевый генератор MORION MV89A с частотой 10 МГц. Оценка фазы производилась по малой выборке из 4·106 отсчетов сигнала с частотой 1 МГц по формуле
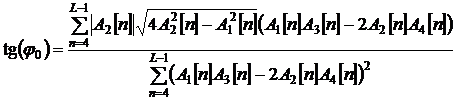 ,
,
где обозначено
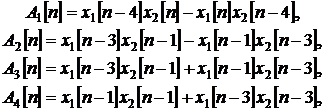
x1, x2 – отсчеты первого и второго сигнала соответственно, L – длина окна. Оцифрованные сигналы перед обработкой предварительно пропускались через цифровой полосовой КИХ фильтр с полосой 20 кГц.
После часового прогрева на оба входа установки подавался один сигнал от прецизионного генератора Г3-122. Динамика отклонения разности фаз от среднего значения, построенная по окну L = 100001, приведена на рис. 1. Дисперсия отклонения разности фаз от среднего значения составила 1,2∙10–4 рад.
Также для формирования входного сигнала использовался генератор прямого цифрового синтеза (DDS) с отдельным опорным генератором MORION MV89A. В этом эксперименте СКО разности фаз от среднего значения составила 1,7∙10–4 рад., динамика разности фаз приведена на рис. 2.
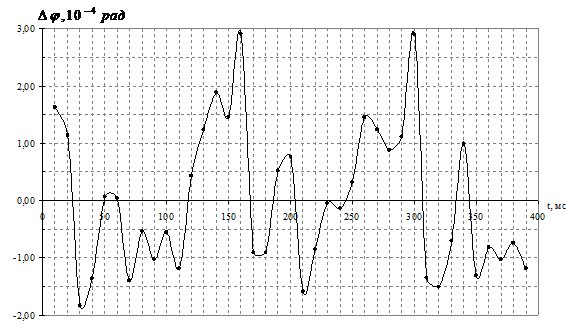
Рис. 1. – Динамика отклонения разности фаз от среднего в эксперименте с Г3-122 (L = 100001)
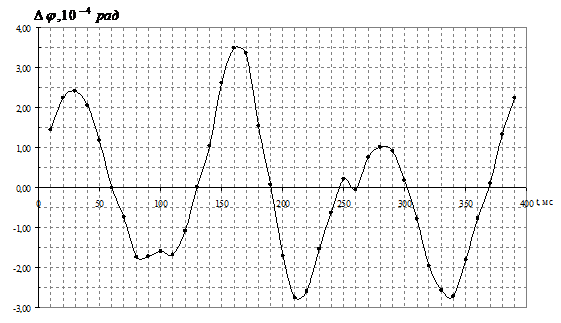
Рис. 2. – Динамика отклонения разности фаз от среднего в эксперименте с DDS с тактированием от разных источников (L = 100001)
В случае, когда и экспериментальная установка, и DDS-генератор тактировались от одного опорного кварцевого генератора, СКО разности фаз составило 3,3∙10–5 рад. Динамика отклонения разности фаз представлена на рис. 3. Проводился аналогичный эксперимент, но в качестве опорного генератора для DDS и установки использовался рубидиевый стандарт частоты 10 МГц FE-5680. В этом случае СКО разности фаз σΔφ = 2,0∙10–5 рад при L = 100001 и σΔφ = 3,7∙10–6 рад. при L = 500001. Динамика разности фаз в этом случае носит практически шумовой характер (рис. 4).
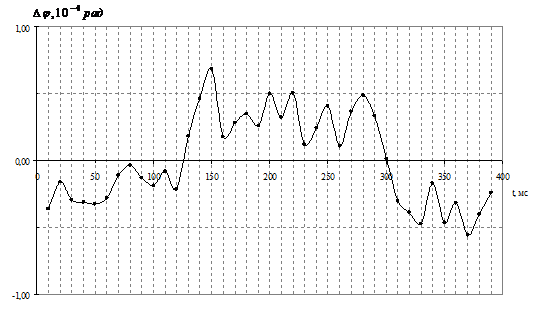
Рис. 3. – Динамика отклонения разности фаз от среднего в эксперименте с DDS с тактированием от одного кварцевого генератора (L = 100001)
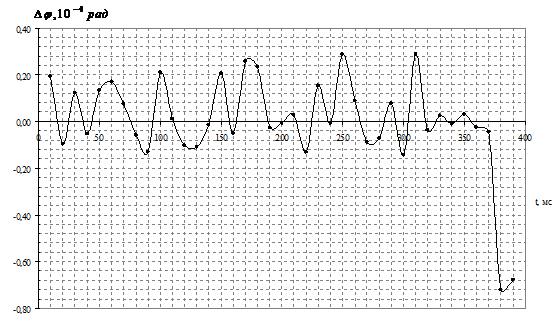
Рис. 4. – Динамика отклонения разности фаз от среднего в эксперименте с DDS с тактированием от одного рубидиевого стандарта (L = 100001)
В эксперименте, в котором тактирование установки и DDS-генератора осуществлялось от двух независимых рубидиевых стандартов, получено СКО разности фаз σΔφ = 1,9∙10–5 рад (L = 100001) и σΔφ = 6,5∙10–6 рад при L = 500001. Динамика разности фаз в этом случае также носит шумовой характер (рис. 5).
Экспериментально были исследованы сигналы имитатора фазового сдвига, принципиальная схема которого приведена на рис. 6. Он представляет собой две RC-цепочки C1C2R1R2, номиналы которых подобраны таким образом, чтобы разность фаз была около π/2. В схеме также установлен геркон SA1, при замыкании которого можно оценить разность фаз усилительного звена имитатора.
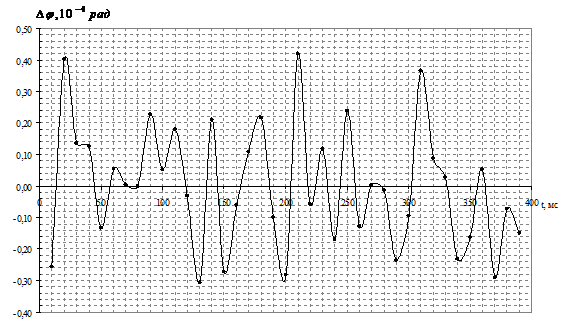
Рис. 5. – Динамика отклонения разности фаз от среднего в эксперименте с DDS с тактированием от разных рубидиевых стандартов (L = 100001)
В эксперименте на имитатор фазового сдвига подавался сигнал частотой 5 МГц от DDS-генератора, его опорным генератором являлся рубидиевый стандарт, а экспериментальная установка тактировалась частотой 25 МГц от генератора АКИП-4113/6. Средняя разность фаз составила <Δφ> = 1,595561 рад, СКО при усреднении по окну длиной L = 100001 в этом эксперименте составила фаз σΔφ = 3,5∙10–4 рад и σΔφ = 6,9∙10–5 рад при L = 500001. Динамика разности фаз приведена на рис. 7. При замыкании геркона получена разность фаз <Δφ> = 0,01896 рад, а СКО σΔφ = 3,9∙10–4 рад (L = 100001) и σΔφ = 6,0∙10–5 рад (L = 500001). Увеличение погрешности экспериментов с имитатором фазового сдвига в первую очередь связано с низкой стабильностью частоты генератора АКИП-4113/6.
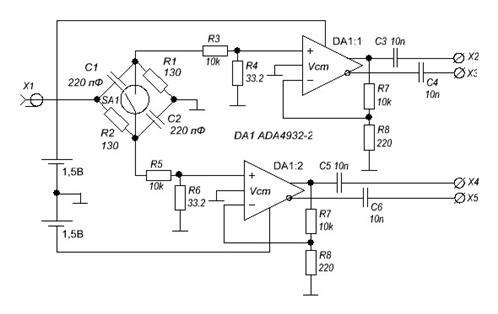
Рис. 6. – Принципиальная схема имитатора фазового сдвига
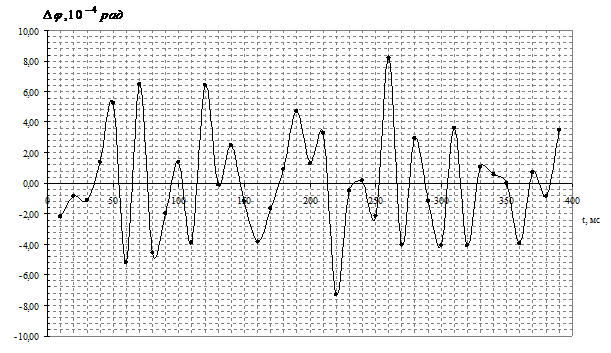
Рис. 7. – Динамика отклонения разности фаз от среднего в эксперименте с имитатором фазового сдвига (L = 100001)
Экспериментальные исследования методов показали, что в лабораторных условиях удается достичь точности измерения фазового сдвига порядка 10–5 рад., на несколько порядков превосходящей Государственную поверочную схему для разности фаз. Также установлено, что ошибка оценивания разности фаз существенно зависит от стабильности опорного генератора. Скорее всего, это связано с фазовым шумом частоты дискретизации, однако этот вопрос требует дальнейших исследований.
Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы (государственные контракты № 14.В37.21.0284, № 14.В37.21.0736).
Литература:
- Popper K. The Logic of Scientific Discovery. London, Hutchinson, 1959. 479 p.
- Безопасность России. Безопасность строительного комплекса./ Н.А. Махмутов, О.И. Лобов, К.И. Еремин. М.: МГОФ "Знание", 2012. 798 с.
- Игнатьев В. К., Никитин А. В., Юшанов С. В. Параметрический анализ колебаний с медленно меняющейся частотой // Известия вузов. Радиофизика. 2010. Т. LIII. № 2. C. 145 – 159.
- Игнатьев В.К., Никитин А.В. Метод медленно меняющейся частоты в радиоволновых измерениях // Журнал радиоэлектроники. 2011. № 11. 20 c. [Электронный ресурс]. Режим доступа http://jre.cplire.ru/jre/nov11/17/text.pdf.
- Боровков В.И., Игнатьев В.К., Никитин А.В., Юшанов С.В. Однозначное определение огибающей и мгновенной частоты электромеханических колебаний // Известия вузов. Электромеханика. 2012. № 1. С. 16 – 20.
- Игнатьев В.К., Невзоров А.А., Орлов А.А. Цифровой протонный магнитометр для измерения геомагнитного поля // Инженерный вестник Дона [Электронный ресурс]. 2013. Т. 24. № 1. С. 92. Режим доступа: http://www.ivdon.ru/uploads/article/pdf/IVD_101_Ignatjev.pdf_1575.pdf, свободный. Загл. с экрана.
- Игнатьев В.К., Козин Д.А., Орлов А.А., Станкевич Д.А. Микромагнитный метод микроструктурного анализа ферромагнитных цилиндрических образцов // Физические основы приборостроения. 2012. № 4. С. 44 – 57.
- Ignatjev V.K., Orlov A.A., Stankevich D.A. Magnetostatics of Cylindrical Ferromagnetic Samples // Physics and Mechanics of New Materials and Their Applications. Brooklyn Polytechnic University, New York, 2013, chapter 7, 450 p.
- Игнатьев В.К. Станкевич Д.А. Дефектоскопия стальной проволоки методом тензорной магнитной топологии [Электронный ресурс] // «Инженерный вестник Дона», 2012. № 2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2012/786 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Шовенгердт Р.А. Дистанционное зондирование. Методы и средства обработки изображений. М.: Техносфера, 2010. 560 с.
- Островский Л.А., Потапов А.И. Введение в теорию модулированных волн. М.: Физматлит, 2003. 400 с.
- Игнатьев В.К., Никитин А.В., Бернардо-Сапрыкин В.Х., Орлов А.А. Измерение разности фаз квазигармонических сигналов в реальном времени // Наука и образование. 2013. № 7. Режим доступа: http://technomag.edu.ru/file/out/608930, свободный. Загл. с экрана.
- Техническая документация на микросхему CYUSB3014 [Электронный ресурс]. Режим доступа: http://www.cypress.com/?docID=44322. Дата обращения 15.09.2013.