Моделирование ab initio электронной структуры слоистых алюмосиликатов

Аннотация

А.С. Каспржицкий, Г.И. Лазоренко, В.А. Явна

Дата поступления статьи: 25.09.2013

Данная работа посвящена исследованию атомной и электронной структуры образцов каолинита (Глуховецкое месторождение) и монтмориллонита (Миллеровское месторождение) методом теории функционала плотности. Проведен анализ применимости существующих обменно-корреляционных потенциалов в приближении локальной плотности (LDA) и обобщенном градиентном приближении (GGA) для адекватного описания физических свойств слоистых алюмосиликатов .Проведено экспериментальное и теоретическое исследование ИК-спектров минералов, а также идентификация наиболее интенсивных полос поглощения, выполненным в приближении ТФП с использованием обменно-корреляционного потенциала PW91. Проведен анализ зонной структуры указанный минералов, который показал, что данные соединения являются прямозонными диэлектриками.

Ключевые слова: ТФП, глины, глинистые минералы, слоистые силикаты, атомная и электронная структура, кристаллические системы, ИК-спектр, зонная струкутра, электронная плотность

01.04.07 - Физика конденсированного состояния

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Слоистые алюмосиликаты являются самыми распространенными на Земле. К ним в первую очередь относятся, в том числе, глинистые минералы, находящие широкое применение в различных сферах строительства, производства и добычи полезных ископаемых. Особенности химического  составаи структуры слоистых минералов позволяют модификацию их физико-механических свойствразличными методами [1-3], что предполагает изучение их физических свойств экспериментальными и теоретическими методами.
В работе представлены результаты abinitoисследования наиболее распространенных глинистых минералов методом теории функционала плотности (ТФП или DFT в английской аббревиатуре) [4,5]. Исследованы образцы глинистого минерала каолинит (Глуховецкое месторождение) и монтмориллонит (Миллеровское месторождение) структура кристаллической ячейки которых приведена нарис.1. Параметры элементарной ячейки каолинита были определены в работе [6], монтмориллонита - [7].
Моделирование электронной структуры выполнено в программном пакете Wien2k [8] в ТФПКона-Шэма. Данное приближение основано на построении электронной плотности ρ(r) системы электронов с использованием спин-орбиталей , полученных в результате решения уравнений вида:
    (1)
с локальным эффективным потенциалом
,
где  кулоновский потенциал (потенциал Хатри), внешний потенциал и  обменно-корреляционный потенциал. 

 

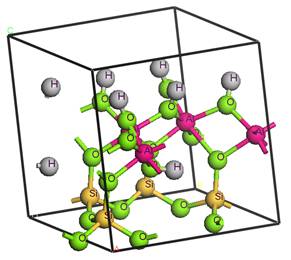
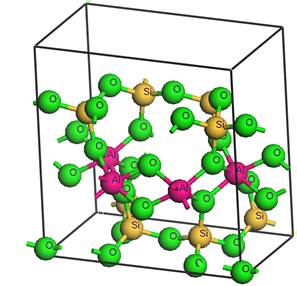
Рис. 1. Кристаллическая структура каолинита (а) и монтмориллонита (б)

Для применения ТФП в расчетах реальных систем важным является используемое приближение для аппроксимации неизвестного обменно-корреляционного функционала (приближение локальнойплотности, градиентное приближение, комбинированные подходы).С вычислительной точки зрения определениеэлектронной структуры в рамках ТФП могут быть существеннооблегчены путем введения в модель псевдопотенциалов. Данные псевдопотенциалы учитывают тот факт, что электроны, находящиеся на сильно связанных заполненных электронных оболочках атомов, практически не изменяют свое состояние при взаимодействиис другими атомами (при образовании и разрыве химических связей и т.п.) Таким образом, при построении моделей возможно разделение электронов на валентные, волновые функций Кона-Шэма которых определяются в ходе расчета, и остовные, описываемые эффективным псевдопотенциалом. При конструировании псевдопотенциалов обычно накладывается условие соответствия волновых функций валентных электронов атома в полноэлектронном и псевдопотенциальном представлении.
В работе проведен анализ применимости существующих обменно-корреляционных потенциалов в приближении локальной плотности (LDA) и

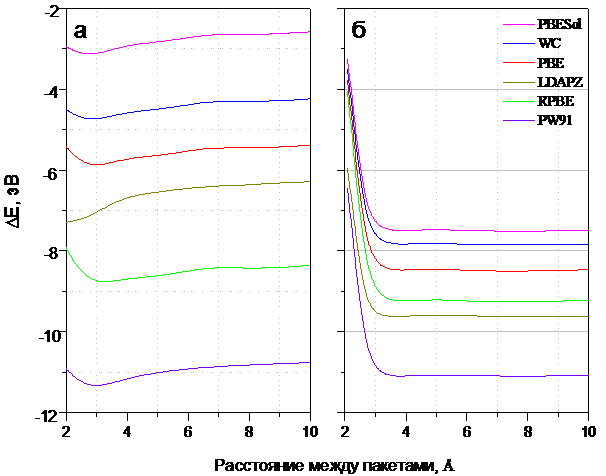
Рис. 2. Зависимость полной энергии кристалла  (в расчете на одну элементарную ячейку) от величины межпакетного пространства для каолинита (а) и монтмориллонита (б).

обобщенном градиентном приближении(GGA): CA-PZ,PBE, RPBE, PW91, WC, PBESOL [9-14] для изучения электронной структуры алюмосиликатов.Для анализа проведен расчет в котором потенциалы ядер и остовных электронов атомов учитывались через предварительно сгенерированные атомные псевдопотенциалы, сохраняющие норму. Блоховские функции электронов в кристалле ищутся в виде разложения по базису плоских волн с энергией отсечки равной 350 эВ. Для генерацииk-точек был использован метод Монкхорста-Пака [15] с сеткой размерностью 3х1x1.Условием сходимости самосогласованных вычислений являлась неизменность полной энергии системы с точностью до 10-5эВ.
Результаты расчета представлены на рис. 2.Анализ потенциальных
кривых показывает, что для обоих типов выбранных минералов полная энергия системы наилучшим образом описывается обменно-корреляционным потенциалом PW91. Дальнейшие исследования свойств минералов выполнены в указанном обменно-корреляционном потенциале.  
На рис. 3 приведена зонная структура каолинита, рассчитанная вдоль высокосимметричных направлений зонной диаграммы E(k), отмеченных точками: G(0,0,0), F (0, 0.5, 0), Q(0, 0.5, 0.5), Z(0, 0, 0.5). Расчет зонной структуры для каолинита показывает, что данный минерал является прямозонным диэлектриком с потолком валентной зоны и дном зоны проводимости в точке G и шириной запрещенной зоны равной 5.2 эВ, что  находится  в  согласии  с данными работы [16]. На этом же рисунке проведены результаты расчетаполных и парциальных плотностей электронных состояний для каолинита (рис.3).
Результаты аналогичных расчетов для монтмориллонита приведены на рис. 4. Расчет зонной структуры выполнен вдоль высокосимметричных направлений, отмеченных точками: L(-0.5,0,0.5), M (-0.5, 0.5, 0.5), A(-0.5, 0, 0), G(0, 0, 0), Z( 0, -0.5, 0.5 ),V( 0, 0, 0.5 ). Анализ результатов расчетов позволяет сделать вывод о том, что данный минерал также является прямозонным диэлектриком с потолком валентной зоны в точке L и дном зоны проводимости в точке G и шириной запрещенной зоны равной 3.7 эВ, что  находится  в  согласии  с данными работы [17]. На этом же рисунке проведены результаты расчета полных и парциальных плотностей электронных состояний для монтмориллонита.
Использованный подход позволил рассчитать  колебательные спектры методом [18]. Для этого выполнен расчет матрицы вторых производных полной энергии системы по координатам, так называемого Гессиана системы:
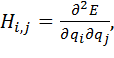(2)
где декартовая координата i – атома системы из Nатомов.

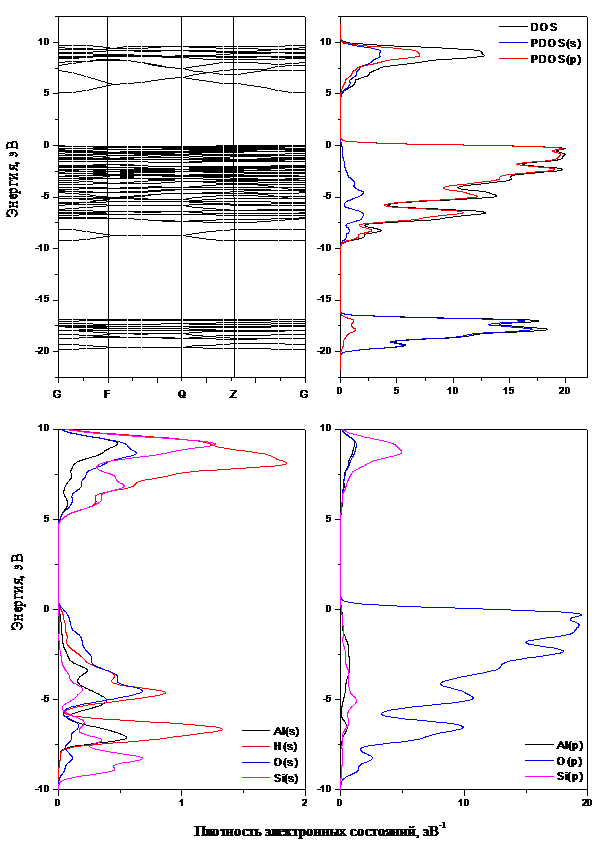
Рис. 3. Зонная диаграмма, зона Бриллюэна с выделенными точками симметрии, а также полная и парциальная плотности электронных состояний для элементарной ячейки каолинита.

Рис. 4. Зонная диаграмма, зона Бриллюэна с выделенными точками симметрии, а также полная и парциальная плотности электронных состояний для элементарной ячейки монтмориллонита.

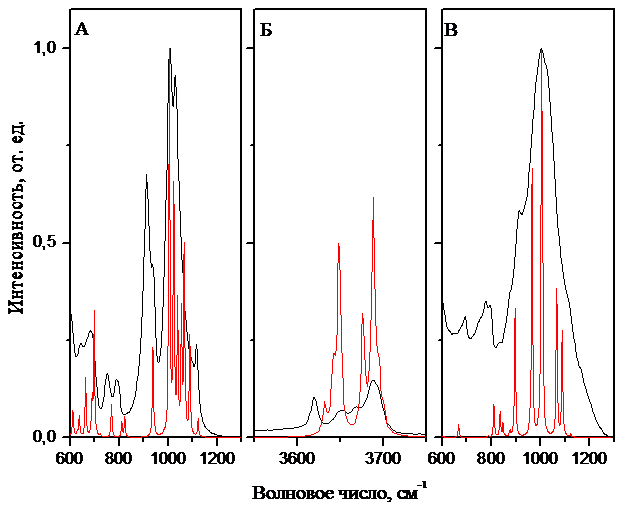
Рис. 5 ИК-спектры каолинита (А, Б) и монтмориллонита (В). Черной линией обозначен экспериментально полученный ИК-спектр, красной линией – результат расчета.  

         Расчет выполнен в обобщенном градиентном приближении(GGA)с потенциалом PW91 с разложением блоховских функции электронов по базису плоских волн с энергией отсечки равной 350 эВ. Для генерации k-точек был использован метод Монкхорста-Пака с сеткой размерностью 3х1x1.
Исследование колебательных спектров в данной работе  экспериментально выполнено с  помощью ИК-Фурье  спектрометра  ALPHA фирмы  BrukerOptics  (BrukerOptikGmbH, Germany) .  Измерение проводили  в  среднем  инфракрасном  диапазоне  от  600  до  4000  см^–1  с  использованием  программного  обеспечения  OPUS.  Образцы  снимались  методом нарушенного полного внутреннего отражения.
Результаты исследований представлены на рис.5. Теоретический расчет находится в хорошем согласии с экспериментом. Анализ спектра частот для каолинита (рис. 5 А) показывает, что появления полос поглощения в  области  1000—1200  см^–1 обусловлено   валентными  колебаниями  связей Si-O и деформационными колебаниями связей О-Н гиббситовогослоя, к ним можно отнести наиболее интенсивные полосы с частотами 1007 и 1029 см^–1.Поглощение в области  900 – 960 см^–1обусловлено деформационными  колебания  ОН-групп  алюмокислородных  октаэдров  каолинита.Группа  пиков  поглощения в  интервале  между  3600  и  3750  см^–1(рис.5 Б) обусловлена  валентными  связямиО-Нгиббситового  слоя в каолините, к ним относятся поглощения на частотах 3618, 3649, 3673 и 3688 см^–1.  Анализ спектра частот для монтмориллонита (рис. 5 В) показал, что наблюдаемая широкая полоса с максимумом 1004 см^-1 обусловлена валентными и деформационными колебаниями  связей Si-O, Al-O. В  частности  полосы  в  области  890 – 970 см^–1  относятся к валентным колебаниям связей Si–OиAl-O, в остальной области до 1200  см^–1присутствуют деформационные колебания связей Si-O. Полученные результаты исследования   ИК-спектроскопии хорошо согласуются с данными работы [19].
В заключение сформулируем основные результаты исследования:
а) в работе методами ТФП изучена атомная и электронная структура наиболее распространённых глинистых минералов каолинита и монтмориллонита;
б) проведен анализ применимости существующих обменно-корреляционных потенциалов в приближении локальной плотности (LDA) и обобщенном градиентном приближении(GGA). Установлено, что для адекватного описания физических свойств указанных алюмосиликатов применим обменно-корреляционный потенциал PW91;
в) анализ зонных диаграмм каолинита и монтмориллонита показывает, что данные соединения являются прямозонными диэлектриками с шириной запрещенной щели 5.2 и 3.7 эВсоответственно, полученные результаты согласуются с существующими данными;
г) методами ИК-спектроскопии проведено исследование каолинита и монтмориллонита. Результаты экспериментального исследования находятся в хорошем согласии с теоретическим расчетомИК-спектра, выполненным в приближении ТФП с использованием обменно-корреляционный потенциал PW91. Проведена идентификация наиболее интенсивных полос поглощения ИК-спектров каолинита и монтмориллонита.

Работа выполнена с использованием ресурсов суперкомпьютерного комплекса МГУ имени М.В. Ломоносова [20] и при поддержке Министерства образования и науки Российской Федерации, соглашение №14.132.21.1666 от 01.10.2012«Информационные и когнитивные технологии определения физико-механических свойств слоистых минералов с наноразмерными добавками».

Литература:

1. Лазоренко, Г.И.Теоретическое исследование влияния нанодобавок на физические свойства монтмориллонитовых глин[Электронный ресурс]// «Инженерный вестник Дона», 2011, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4y2011/523(доступ свободный) – Загл. с экрана. – Яз.рус.
2. Gonsalves К.Е., Chen X.   Inorganic nanostructured materials [Текст]//Nanostructured materials», 1996. – V.5. – P. 3256-3262.
3. Mark J.E. Ceramic reinforced polymers and polymer-modified ceramics[Текст]//Polym. Eng. Sci.,1996. –  №36. – P. 2905-2920.
4. Hohenberg P., Kohn W. Inhomogeneous Electron Gas [Текст]// Phys. Rev. B.,1964. – V.136. – P. 864 – 871.
5. Kohn W.,Sham L. J. Self–Consistent Equations Including Exchange and Correlation Effects [Текст] // Phys.Rev. A.,1965. – V.140. – P. 1133 – 1138.
6. Каспржицкий А.С., Лазоренко Г.И., Морозов А.В., Явна В.А.Идентификация структурных особенностей слоистых минералов методом рентгеновскойдифрактометрии[Электронный ресурс]  // «Инженерный вестник Дона», 2012, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1406(доступ свободный) – Загл. с экрана. – Яз.рус.
7. Kasprzhitsky A., Lazorenko G., Yavna V., Talpa B. Mineralogical characterization of bentonite clay from Millerovo field [Текст] // Proceedings of the 2nd International Conference Clays, Clay Minerals and Layered Materials – CMLM2013 St Petersburg, 11-15 September, 2013
8. Blaha P., Schwarz K., Sorantin P. Full-potential, linearized augmented plane wave programs for crystalline systems [Текст]// Computer Physics Communications, 1990. –  V. 2., – p.399-415.
9. Ceperley D. M., Alder B. J. Ground State of the Electron Gas by a Stochastic Method [Текст]// Phys. Rev. Lett., 1980. –  V.45, – P.566-569.
10. Perdew J.P., Burke K.,ErnzerhofM. Generalized Gradient Approximation Made Simple [Текст]// Phys. Rev. Lett., 1996. –  V.77, – P.3865-3868.
11. Hammer B., Hansen L. B., Norskov J. K.  Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhoffunctionals [Текст] //  Phys. Rev. B, 1999.–  V.59, – P.7413-7421.
12. Perdew J. P.,Chevary J. A.,VoskoS. H., Jackson K. A., Pederson M. R., Singh D. J.,Fiolhais C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation [Текст]//  Phys. Rev. B, 1992. – V.46, – P.6671-6687.
13. Wu Z., CohenR. E. More accurate generalized gradient approximation for solids [Текст]//  Phys. Rev. B, 2006. –  V. 73 (235116) – P. 1-6.
14. PerdewJ. P., Ruzsinszky A., Csonka G. I., Vydrov O.A., Scuseria   G. E., Constantin L. A., Zhou X., Burke K.Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces [Текст]// Phys. Rev. Lett., 2008. –  V. 100 (136406), – P.1-4.
15. Monkhorst H. J., Pack J. D. Special points for Brillouin-zone integrations [Текст]// Phys. Rev. B., 1976. – V. 13. – P. 5188–5192.
16. Zhao Q.-j., Yang Q.-f., Chen Q.-y., Yin Z.-l., Wu Z.-p., Yin Z.-g. Behavior of silicon-containing minerals during Bayer digestion [Текст] // Trans. Nonferrous Met.Soc. China, 2010. –P. s1–s9.
17. He M.-C., Fang Z.-J., Zhang Ping Atomic and electronic structures of montmorillonite in soft rock [Текст] // Chinese Physics B, 2009. –V.18 –P. 2933–2937.
18. Wilson, E. B. Molecular Vibrations [Текст]: Монография/ E. B.Wilson,  J. C. Decius, P. C.  Cross – New York: Dover, 1955. –  388 p.
19. Etienne B., Saitta A.M., Mauri F., Calas G. First-principles modeling of the infrared spectrum of kaolinite [Текст] // American Mineralogist, 2001. –V.86 –P. 1321–1330.
20. ВоеводинВл.В., Жуматий С.А., Соболев С.И., Антонов А.С., Брызгалов П.А., Никитенко Д.А., Стефанов К.С., Воеводин Вад. В. Практика суперкомпьютера «Ломоносов» [Текст]// Открытые системы. - Москва: Издательский дом «Открытые системы», 2012. –  №1. – С.31-36.