Алгоритм расчта отражений на основе геометрической модели

Н.В. Благородова; А.А. Замятин; В.В. Сухомлинова

Алгоритм расчёта отражений на основе геометрической модели

Аннотация

Н.В. Благородова, А.А. Замятин, В.В. Сухомлинова

Предложен алгоритм построения отражений от экранов сложной формы. Геометрическое моделирование на основе предложенного алгоритма позволяет проводить экспресс-оценку противопожарных расстояний между зданиями сложной геометрии, а также между технологическим оборудованием, которое характеризуется выделением тепла. Приведены аналитические зависимости, описывающий процесс построения отражений, программные алгоритмы и примеры вычислений.

Ключевые слова: геометрическое моделирование, геометрическая оптика, геометрическая акустика, законы отражения

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Размер минимальных противопожарных расстояний между зданиями городской и промышленной застройки, а также безопасные разрывы между технологическим оборудованием, излучающим тепло, назначаются действующими нормами проектирования в области пожарной и промышленной безопасности. Рекомендуемые нормативные расстояния справедливы на 100% для расположенных строго параллельно элементов простой геометрической формы. При определении рекомендуемых нормами размеров минимальных противопожарных расстояний между зданиями используется классическая теория передачи тепла излучением. При этом учитывается только действие лучистой энергии. Распространение пожара от теплоты, передаваемой конвекцией, от горящих конструктивных элементов и искр, перебрасываемых ветром и нагретым воздухом, не учитывается. Это объясняется тем, что количество теплоты, передаваемое конвекцией, составляет небольшой процент по сравнению с теплотой, передаваемой излучением.

В расчетах лучистой энергии, на наш взгляд, значительный вклад в общую картину вносят первые отражения. На практике, при решении задач, связанных с расчётами лучистой энергии, целесообразно применять геометрическую модель. Эта модель даёт хорошие результаты в тех случаях, когда можно пренебречь волновыми свойствами излучения. В данной модели не рассматриваются явления интерференции, дифракции и др., связанные с волновыми свойствами излучения [1].

Как известно, падающий и отражённый лучи лежат в одной плоскости с нормалью к поверхности, построенной в точке падения, и составляют с ней равные углы. Рассмотрим алгоритм построения отражённого луча при данных источнике и точке падения на отражающей поверхности.

Пусть задана поверхность  уравнением 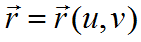. В пределах рассматриваемого отсека поверхность не имеет особых точек. На поверхности задана точка А, её радиус-вектор равен 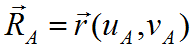, задан источник излучения, находящийся в точке I (рис.1). Вектор нормали к поверхности  в точке А определим по формуле

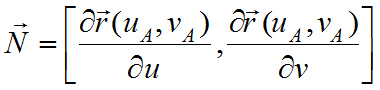. (1)

Как уже отмечалось, падающий, отражённый лучи и нормаль к поверхности лежат в одной плоскости. Обозначим эту плоскость через П_l (рис. 1) и будем называть лучевой плоскостью. Вектор нормали лучевой плоскости

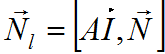. (2)

Сделаем такое преобразование координат, чтобы лучевая плоскость П_l в новой системе координат стала фронтальной плоскостью уровня [2].

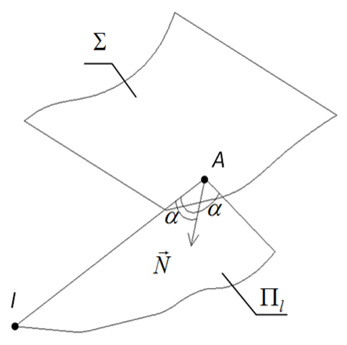
Рис. 1. Геометрическая модель отражения

Определим угол, составляемый горизонтальной проекцией вектора нормали П_l с осью Oy – угол γ:

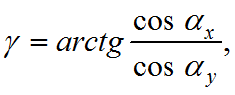(3)

где cos _x и cos _y направляющие косинусы вектора 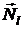по осям Ox и Oy, равные

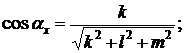
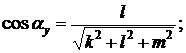
k, l, m – координаты вектора .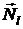

Определим угол, составляемый 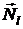с плоскостью xOy:

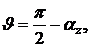(4)

где _z – угол, составляемый 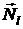с осью Oz, равный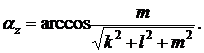

Повернем систему координат вокруг оси Oz на угол γ (рис.2). В новой системе координат вектор нормали плоскости П_l будет лежать в координатной плоскости yOz. Матрица данного преобразования имеет вид:

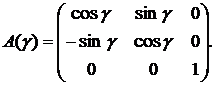(5)

Повернем систему координат вокруг оси Ox на угол ϑ (рис.2).

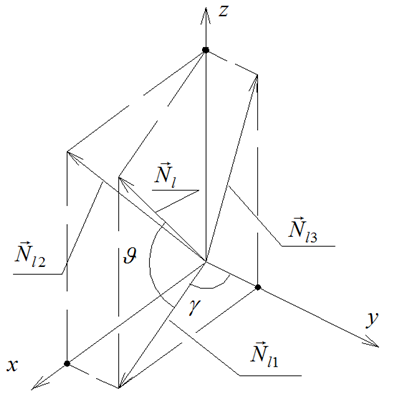
Рис. 2. Углы, составляемые вектором нормали лучевой плоскости с осями и плоскостями проекций

В новой системе координат вектор нормали П_l параллелен оси Oy. Следовательно, в этой системе координат П_l является фронтальной плоскостью уровня. Матрица этого преобразования имеет вид:

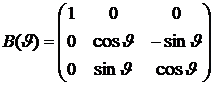. (6)

Получим матрицу суммарного преобразования, умножив A(γ) (5) на B(ϑ) (6)

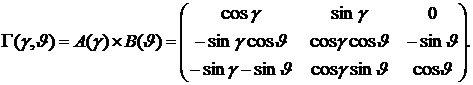(7)

Найдем координаты точек I, A и вектора 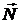в системе координат, в которой П_l является плоскостью уровня. Координаты найдем по соотношению

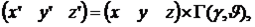(8)

где x, y, z – координаты соответствующей точки в исходной системе координат, x’, y’, z’ – ее координаты в новой системе координат. Т.к. П_l, после преобразования, является фронтальной плоскости уровня, то все ее точки имеют y’=const и трехмерная задача сводится к двумерной.

Сдвинем начало системы координат в точку A. Координаты точек определим по соотношению

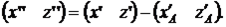, (9)

Где x’_A, z’_A координаты точки A. Повернем систему координат таким образом, чтобы ось O’’’z’’’ совпала с вектором .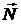

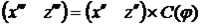, (10)

где 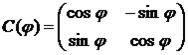– матрица преобразования, ,

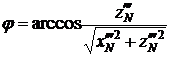x’’’_N ,z’’’_N – координаты вектора .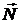

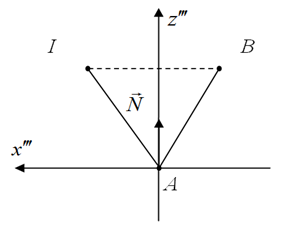
Рис. 3. Построение отраженного луча

В новой системе координат найдем координаты точки B, которая будет определять, совместно с точкой A, отраженный луч. Её координаты равны (рис. 3)

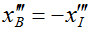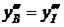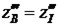, , . (11)

Выполним обратные преобразования, чтобы определить координаты точки B в исходной системе координат

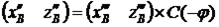; (12)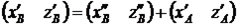; (12)

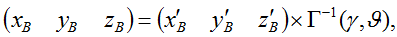(13)

где Г^-1(γ , ϑ)– матрица обратного преобразования по отношению к (7), равная

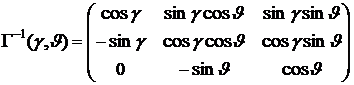Программный алгоритм построения отраженного луча имеет линейную структуру, которая заключается в последовательности выполнении вычислений и преобразований, описанных выше. Программное обеспечение разрабатывалось в среде ObjectARX в среде AutoCAD [3]. Отражающие поверхности аппроксимировались методом Фергюсона [4,5]. Пример вычислений приведен на рис. 4. На рис. 4 показаны отраженные от поверхности Ω лучи, исходящие из источника, расположенного в точке I.

Данный алгоритм может быть использован в качестве модуля различных автоматизированных систем, для расчетов вклада первых отраженных лучей в суммарную энергию излучения, в том случае, если допускается применение геометрической модели для описания процессов отражения.

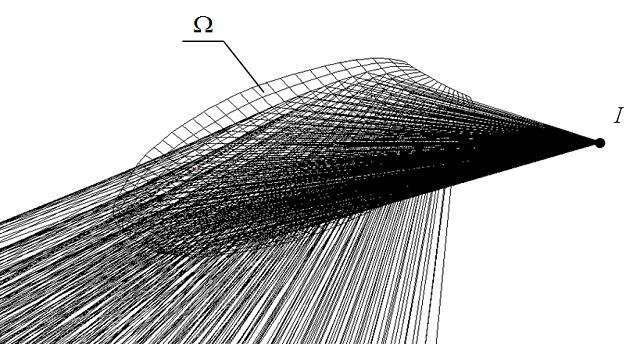Рис. 4. Пример расчета

Библиографический список

Ландсберг Г.С. Оптика / Г.С. Ландсберг. – Москва: Наука, 2003. – 848 с.
Замятин А.В. Алгоритм построения точек пересечения нелинейчатых поверхностей. Электронный журнал №3 2010. Электрон. ресурс. Режим доступа: http://www.ivdon.ru/ (дата обращения 29 апреля 2012).
Полищук Н.Н. AutoCAD: разработка приложений, настройка и адаптация / Н.Н. Полищук. – Санкт-Петербург: БХВ – Петербург, 2006. – 992 с.
Роджерс Д., Адамс Дж. Математические основы машинной графики / Д. Роджерс, Дж. Адамс. – Москва: Мир, 2001. – 604 с.
5. Замятин А.В., Сухомлинова В.В. Аппроксимация порции поверхности по методу Фергюсона / Известия вузов. Северо-Кавказский регион. Технические науки. Приложение №2, 2006г.