Модификация метода Прони при приеме сигналов векторно-скалярной антенной
Аннотация
Приводится алгоритм, позволяющий применять метод Прони для оценки параметров шумящих источников с использованием векторно-скалярной приемной антенны. Помехоустойчивость предложенного алгоритма достаточно высока, так как измеренные компоненты акустического поля не содержат шумовой составляющей.
Ключевые слова: метод Прони, векторно-скалярная антенна, динамический шум моря, ковариация, поток мощности
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Модификация метода Прони при приеме сигналов векторно-скалярной антенной
Т.Н. Ларина, Г.М. Глебова , Е.В. Винник
, Е.В. Винник
Ростовский государственный строительный университет,
 Научно-исследовательский институт физики Южного федерального университета,
Научно-исследовательский институт физики Южного федерального университета,
г. Ростов-на-Дону
Хорошо известный параметрический метод Прони является методом восстановления квазиполинома по конечному числу его значений на равномерной сетке временных или пространственных отсчетов [1-3]. Метод Прони использует представление наблюдаемого процесса в виде комплексного экспоненциального ряда. Метод позволяет по отсчетам сигнала найти параметры этих комплексных экспонент, что, в свою очередь, дает возможность записать выражение для спектральной или пространственной плотности исследуемого сигнала. Широкое применение метода Прони стало возможным только в последнее время, поскольку он существенно не линеен и требует больших вычислительных затрат. В прикладных задачах гидроакустики метод применяется как для оценки спектра принимаемых сигналов, так и для определения угловых координат сигналов от локальных источников. Модификация метода для определения параметров коррелированных сигналов или нормальных волн, образующих акустическое поле источника в волноводе предложена в работе [4].
В данной работе предлагается модификация метода для оценки угловых координат источника с использованием векторно-скалярной антенны. Актуальность такого похода связана с техническими достижениями в области конструирования и создания векторных приемников, измеряющих колебательную скорость частиц. Кроме того имеется еще одно обстоятельство, которое определяет необходимость разработки и исследования алгоритмов для векторно-скалярных антенн, работающих на фоне шумов моря, а именно, среднее значение потока мощности шума в горизонтальной плоскости равно нулю. Таким образом, алгоритмы обработки для векторно-скалярных антенн, использующие в своей основе поток мощности, должны обладать повышенной помехоустойчивостью.
В данной работе рассматривается линейная эквидистантная векторно-скалярная антенна, каждый модуль которой содержит приемник давления и два приемника колебательной скорости, оси которых расположены в горизонтальной плоскости. Принимаемые сигналы на 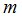 -ом модуле ВСА можно представить в виде:
-ом модуле ВСА можно представить в виде:
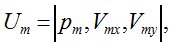
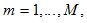 (1)
(1)
здесь 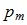 ,
, 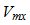 , и
, и 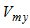 - звуковое давление и проекции колебательной скорости по направлениям
- звуковое давление и проекции колебательной скорости по направлениям 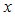 и
и 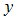 измеряемые
измеряемые 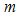 -ым приемным модулем. Размерность вектора
-ым приемным модулем. Размерность вектора 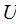 равна
равна 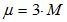 , т.е. величина
, т.е. величина 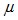 фактически определяет число приемных элементов в антенне. Для источника, давление которого на
фактически определяет число приемных элементов в антенне. Для источника, давление которого на 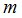 -ом модуле равно
-ом модуле равно
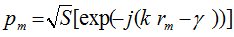 , (2)
, (2)
с использованием направляющих косинусов, как весов для компонент колебательной скорости, вектор измеряемых величин 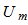 можно представить в виде
можно представить в виде
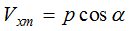 ,
,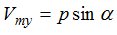 ,
, 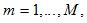 (3)
(3)
здесь 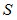 - мощность сигнала на приемнике давления,
- мощность сигнала на приемнике давления,  - волновое число, -
- волновое число, -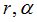 - координаты источника в полярной системе координат,
- координаты источника в полярной системе координат, 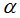 - пеленг источника отсчитывается от оси Х. В работе [5] теоретически и экспериментально показано, что представление сигналов в виде (3) справедливо как при распространении сигналов в свободном пространстве, так и в волноводе.
- пеленг источника отсчитывается от оси Х. В работе [5] теоретически и экспериментально показано, что представление сигналов в виде (3) справедливо как при распространении сигналов в свободном пространстве, так и в волноводе.
Для гауссовых сигналов и шумов с нулевым математическим ожиданием статистика измерений полностью определяется матрицей ковариаций, которая рассчитывается для заданной модели сигналов и помех как K=U∙U* , символ «*» означает эрмитово сопряжение. Матрица К размером 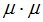 имеет блочно-диагональный вид:
имеет блочно-диагональный вид:
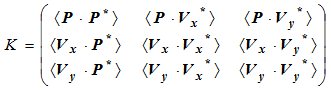 , (4)
, (4)
и представляет собой сумму сигнальной матрицы - 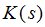 и матрицы помех -
и матрицы помех - 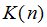
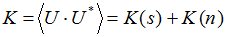 . (5)
. (5)
Каждый из трех диагональных блоков этой матрицы описывает ковариационные зависимости между одноименными компонентами векторно-скалярного поля, а недиагональные блоки – их взаимную ковариацию.
Метод Прони является «быстрым» методом решения системы уравнений следующего вида:
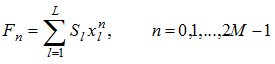 , (6)
, (6)
где 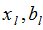 — неизвестные комплексные величины (2∙L<M). Неизвестные
— неизвестные комплексные величины (2∙L<M). Неизвестные 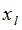 находятся как корни полинома
находятся как корни полинома
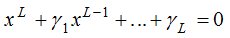 , (7)
, (7)
коэффициенты которого удовлетворяют системе линейных уравнений
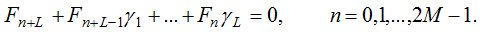 (8)
(8)
После нахождения величин 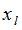 ; значения их подставляют в (6) и решают полученную линейную систему уравнений относительно
; значения их подставляют в (6) и решают полученную линейную систему уравнений относительно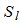 .
.
Применительно к скалярной антенне измеряемые величины 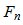 - это элементы ковариационной матрицы (4), соответствующие верхнему диагональному блоку
- это элементы ковариационной матрицы (4), соответствующие верхнему диагональному блоку 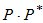 матрицы К, значение величины
матрицы К, значение величины 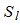 соответствует мощности l-ого локального источника,
соответствует мощности l-ого локального источника, 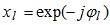 , где
, где 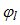 — разность фаз сигнала от l-ого локального источника в двух соседних приемных элементах. Угол
— разность фаз сигнала от l-ого локального источника в двух соседних приемных элементах. Угол 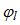 связан с пространственным углом прихода сигнала от l-ого локального источника соотношением
связан с пространственным углом прихода сигнала от l-ого локального источника соотношением 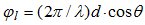 , где
, где 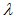 — длина волны,
— длина волны, 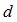 — расстояние между соседними элементами эквидистантной приемной антенны.
— расстояние между соседними элементами эквидистантной приемной антенны.
Рассмотрим возможность модификации метода Прони при приеме сигналов векторно-скалярной антенной. В качестве измеренных величин возьмем элементы двух подматриц матрицы 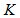 :
: 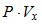 и
и 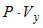 , элементы которых обозначим
, элементы которых обозначим 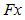 и
и 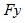 , соответственно. Выражение (6) преобразуется к виду
, соответственно. Выражение (6) преобразуется к виду
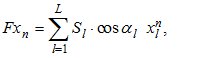
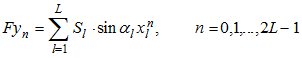 . (9)
. (9)
Введем обозначения:
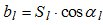 и
и 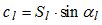
тогда (9) можно представить в виде, идентичном (7), для которого применима схема нахождения неизвестных параметров сигналов по методу Прони
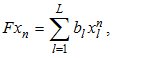
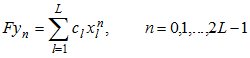 . (10)
. (10)
Поскольку значения коэффициентов 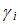 , можно определить как из системы уравнений для
, можно определить как из системы уравнений для 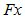 так и для
так и для 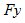 , то в общем случае для определения
, то в общем случае для определения 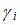 целесообразно составить совместную переопределенную систему уравнений, которую решают методом наименьших квадратов. Совместное использование измерений повышает точность определения коэффициентов
целесообразно составить совместную переопределенную систему уравнений, которую решают методом наименьших квадратов. Совместное использование измерений повышает точность определения коэффициентов 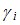 при работе в реальных условиях, характеризующихся наличием шумов, конечным временем наблюдения и ограниченными размерами приемной антенны. По коэффициентам
при работе в реальных условиях, характеризующихся наличием шумов, конечным временем наблюдения и ограниченными размерами приемной антенны. По коэффициентам 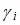 , составляют полином (7) и находят корни
, составляют полином (7) и находят корни 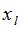 . Значения
. Значения 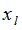 подставляют в системы уравнений (9) и определяют
подставляют в системы уравнений (9) и определяют 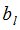 и
и 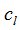 . А затем по найденным значениям
. А затем по найденным значениям 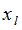 ,
, 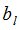 и
и 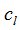 оценивают искомые параметры сигналов от локальных источников: фазовые углы
оценивают искомые параметры сигналов от локальных источников: фазовые углы 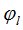 и мощность сигналов
и мощность сигналов 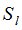
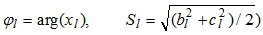 . (11)
. (11)
Преимущество использования подматриц, измеряющих поток мощности в горизонтальной плоскости очевидно, так как среднее значение потока мощности динамического шума моря в данном случае равно нулю. В то время как для матриц вида 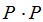 ,
, 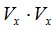 и
и 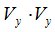 шум присутствует как на диагональных элементах матрицы, так и недиагональных, поскольку эти компоненты поля коррелированны по пространству. В дальнейшем необходимо детально исследовать данный метод с точки зрения оптимальности его математической реализации, а также потенциальной устойчивости к флуктуациям шумов моря и пространственной неоднородности, обусловленной дальним судоходством, ветровым волнением, береговым прибоем и прочими факторами.
шум присутствует как на диагональных элементах матрицы, так и недиагональных, поскольку эти компоненты поля коррелированны по пространству. В дальнейшем необходимо детально исследовать данный метод с точки зрения оптимальности его математической реализации, а также потенциальной устойчивости к флуктуациям шумов моря и пространственной неоднородности, обусловленной дальним судоходством, ветровым волнением, береговым прибоем и прочими факторами.
Литература
1. Prony G.R.B. Essai experemenal et analytique: sur les lois de la dilitabilite de fluids elastques et sur celles de la force expanslve de la vapeure de l’eau et la vapeure de l’alkool, a differentes temperatures. //J. de L’Ecole Polytechnique. –1795. – T.1. –24-76.
2. Марпл С.П. Цифровой спектральный анализ и его приложения. –М. –Мир. –1990.
3. Backer H.P. Cjmparison of FFT and Prony algorithm for bearing estimation of narrow-band signals in a realistic ocean environment. // – JASA. – Mar. – 1977. – V.61. – P. 756-762.
4. Гительсон В.С., Глебова Г.М., Кузнецов Г.Н. Определение параметров коррелированных сигналов с использованием метода Прони. // Фкустический журнал. – 1988. – Т.XXXIV. – 1. – 170-172/
5. Гордиенко В.А. Векторно-фазовые методы в акустике. –М.: –ФИЗМАТЛИТ, –2007. – 480 с.