Причины возникновения интервальных значений в математических моделях исследования робастной устойчивости систем управления
Аннотация
Рассматриваются исторически сложившиеся этапы в развитии теории исследования систем управления с неопределенностями, причины их возникновения в математической модели, что находит отражение в возникновении интервальных значений в передаточной функции объекта управления. Предлагается алгоритм получения экспериментальным путем этих интервальных значений.
Ключевые слова: интервальные значения, робастная устойчивость, передаточная функция, параметрическая неопределенность, математическая модель, системы управления
05.13.18 - Математическое моделирование, численные методы и комплексы программ
В настоящее время в центре внимания специалистов теории автоматического управления находятся проблемы исследования динамических свойств не полностью определенных объектов.
Проблема неопределенности, возникающая на всех этапах жизни систем управления (СУ) начиная от момента её проектирования и заканчивая этапом эксплуатации, вносит различные неучтенные факторы, влияющие на условия функционирования данной системы. Известное определение неопределенности описывает её как признак, имеющий несформированность величинных характеристик, в которых отсутствуют точные значения. Появление неопределенности может быть обусловлено несколькими причинами, среди которых можно назвать незнание истинных значений параметров объекта управления, их непредсказуемое изменение во времени или наличие неконтролируемых возмущений, осуществляющих воздействие на систему управления.
В исторической ретроспективе можно выделить ключевые этапы, которые отражают определенные вехи в развитии теории для исследования СУ с неопределенностями, среди которых можно выделить следующие:
1. Предложена одна из первых моделей неопределенности (нелинейная), отраженная в работах А.И. Лурье [1], М.А. Айзермана [2], Ф.Р. Гантмахера [2].
2. Предложены И. Горовицем [3] и А.М. Мейлахсом [4] модели линейных систем с параметрической неопределенностью.
3. Осуществлен анализ неопределенности, связанных с моделью неизвестных, но ограниченных возмущений А.Б. Куржанским [5] и Ф. Л. Черноусько [6].
4. Разработаны вероятностный подход к исследованию робастности [7], а также модели частотной неопределенности [8], интенсивно изучаемые еще с 80 –х годов.
5. Впервые рассмотрена S. Faedo [9] задача об устойчивости интервального семейства полиномов, обосновавшего достаточные условия робастной устойчивости, используя интервальный аналог алгоритма Рауса.
6. Затронута Л. Заде и Ч. Дезоером [10] проблема робастной устойчивости линейных систем.
7. Опубликована работа В.Л. Харитонова [11], сформулировавшего критерий устойчивости интервального семейства полиномов.
8. Осуществлено доказательство реберной теоремы, A.C. Барлетом, C.В. Холотом и Х. Лином [12].
9. Опубликован графический критерий робастной устойчивости полиномов, доказанный Б.Т.Поляком и Я.З.Цыпкиным [13].
Для исследования нелинейных и нестационарных систем управления с неопределенностями, разработаны методы адаптивного, робастного управления, нечеткой логики или нейросетевых регуляторов [14,15]. В последнее время широкое распространение получили методы исследования робастной устойчивости динамических объектов [16], что позволяет, на этапе проектирования, определить, является ли устойчивым весь класс рассматриваемых систем.
Среди причин возникновения неопределенностей, которые приводят к нарушению условий эксплуатации объектов управления и возникновения интервальных коэффициентов в математической модели можно назвать следующие:
1. Неточность моделей, возникающих из-за линеаризации, дискретизации, погрешностей при выводе уравнений ввиду большой сложности исследуемого или проектируемого объекта.
2. Недостаточная степень учета особенности эксплуатации СУ и проявляющиеся при этом изменения отдельных параметров.
3. Ошибки, возникающие в различного рода датчиках, приводящие к погрешностям и задержкам прохождения сигналов.
4. Различные непредвиденные воздействия на СУ.
Обычно при исследовании СУ рассматриваются непараметрическая неопределенность, вызванная неполнотой знания аналитической структуры уравнений модели объекта, и параметрическая неопределенность, обусловленная неточным знанием значений некоторых параметров СУ. Параметрическая неопределенность является наиболее хорошо изученной и для неё разработаны большое количество методов исследования СУ, причем данная неопределенность как раз позволяет получить интервальные значения в коэффициентах числителя и знаменателя передаточной функции при составлении математической модели.
Таким образом, ошибки, возникающие при моделировании, содержат:
- ошибки модели;
- ошибки численного метода;
- ошибки в исходных данных.
Известно процентное соотношение, приведенных ошибок, которое проявляется из-за неточности модели и составляет 14-15%, из-за неточности численного метода – 2-3% и из-за неточности исходных данных – 82-84%.
Так как, неточности исходных данных составляют подавляющее большинство неопределенности, то необходимо для исследования робастной устойчивости СУ с таким видом неопределенности, использовать интервальные методы.
Поэтому возникает необходимость решения следующих задач:
1. Разработки методик получения интервальных математических моделей, позволяющих обеспечить синтез законов регулирования (управления).
2. Оценки адекватности полученной интервальной модели, гарантирующей существование решения задачи управления в условиях неопределенности.
Для получения коэффициентов интервальных значений полиномов в числителе и знаменателе предлагается следующий алгоритм, представленный на рис. 1.
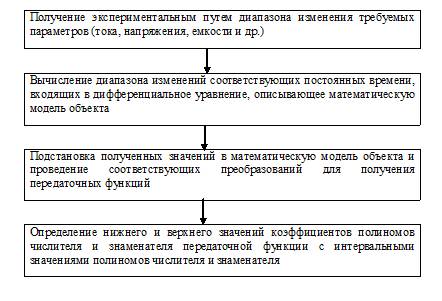
Рис.1. Алгоритм получения передаточной функции с интервальными значениями коэффициентов
Приведенный алгоритм позволяет получить интервальные значения коэффициентов полиномов числителя и знаменателя передаточной функции, как для одного изменяемого параметра, так и для нескольких параметров, изменяющихся одновременно.
Таким образом, использование предложенного алгоритма получения передаточной функции с интервальными значениями коэффициентов и разработка соответствующих методик исследования интервальных математических моделей, позволит решить задачу робастной устойчивости объекта управления.
Литература
1. Лурье, А.П. Некоторые нелинейные задачи теории автоматического регулирования [Текст]:Монография / А.П. Лурье. – М.: Гостехиздат. 1951.
2. Айзерман М. А.,Гантмахер Ф. Р. Абсолютная устойчивость регулируемых систем. [Текст]: Монография / М. А. Айзерман, Ф.Р. Гантмахер — М.: АН СССР, 1963.
3. Горовиц И. Синтез систем с обратной связью. [Текст]: Монография / И. Горовиц. – М.: Советское радио, 1970.
4. Мейлахс, А. М. О существовании функции Ляпунова для параметрических возмущенных линейных систем / Сложные системы управления. [Текст]: Монография / А. М. Мейлахс. — Киев: ИК АН УССР, 1980.
5. Куржанский, А.Б. Управление и наблюдение в условиях неопределенности. [Текст]: Монография / А.Б. Куржанский. — М., Наука, 1977.
6. Черноусько Ф. Л., Колмановский В. Б. Оптимальное управление при случайных возмущениях. [Текст]: Монография / Ф. Л. Черноусько, В. Б. Колмановский. — М.: Физматлит, 1978.
7. Хьюбер, П. Робастность в статистике. [Текст]: Монография / П. Хьюбер. М.: Мир, 1984.
8. Гелиг А.Х., Леонов Г.А., Якубович В.А. Устойчивость нелинейных систем с неединственным положением равновесия. [Текст]: Монография / А.Х. Гелиг, Г.А. Леонов, В.А. Якубович. М.: Наука, 1978.
9. Faedo S. Un nuova problema di stabilita per le equazione algebriche a coefficienti reali // Ann. ScuolaNorm. Super. Piza, Ser. sci. fis. e mat. 1953. V. 7, No. 1 -2. P. 53 63.
10. Заде Л., Дезоер Ч. Теория линейных систем. [Текст]: Монография / Л. Заде, Ч. Дезоер. М.: Наука, 1970.
11. Харитонов В.Л. Асимптотическая устойчивость семейства систем линейных дифференциальных уравнений. [Текст] // Дифференц. уравнения. 1978. Т. 14. №11.
12. Bartlett A.C., Hollot C.V., Lin H. Root location of an entire polytope polynomials: it suffices to check the edges // Proc. Amer. Contr. Conf. − Minneapolis: MN, 1987.
13. Поляк Б. Т., Цыпкин Я. 3. Частотные критерии робастной устойчивости и апериодичности линейных систем. [Текст] // Автоматика и телемеханика, 1990, № 9. С. 91–104.
14. Методы робастного, нейро-нечеткого и адаптивного управления. Под редакцией Н.Д. Егупова. [Текст]: Монография / Изд. МГТУ им. Н.Э. Баумана. 2002.
15. Никифоров, В.О. Адаптивное и робастное управление с компенсацией возмущений. [Текст]: Монография / В.О. Никифоров. СПб.: Наука, 2003.
16. Целигоров Н.А., Целигорова Е.Н. Алгебраические аспекты исследования робастной абсолютной устойчивости многомерных систем управления. [Текст] Материалы Четвертой научной конференции «Системный синтез и прикладная синергетика». – Таганрог: Изд-во ТТИ ЮФУ, 2011, 348-357с.