Определение углов полной рефракции при больших зенитных расстояниях
Аннотация
Получена формула для определения углов полной рефракции при больших зенитных расстояниях. Выполнено исследование точности определения углов полной рефракции по полученной формуле для зенитных расстояний 890 и 900 для условий стандартной атмосферы ГОСТ 4401-81.
Ключевые слова: Геодезия, Рефракция, Атмосфера
Обычно при получении формул углов рефракции полагают, что атмосфера является сферической, и слои газовой среды или воздуха одинакового коэффициента преломления (изодиоптрические слои) являются сферами с центром, совпадающим с центром Земли. Полагаемое для такой модели дифференциальное уравнение угла полной рефракции имеет вид:
 (1)
(1)
где φ – угол между радиусом сферы и направлением оптического луча в текущей точке; n – коэффициент преломления газовой среды или воздуха, ρ” = 206265” [1].
Недостатком этого уравнение является то, что при φ = 900 dφ = ∞, хотя известно, что в горизонте угол астрономической рефракции равен не бесконечности, а примерно 35’. Поэтому выражение (1) используют обычно при углах φ, отличающихся от 900. Кроме того, при статическом состоянии атмосферы изодиоптрические поверхности обычно совпадают с уровенными, положение которых в пространстве более точно аппроксимируется поверхностями, параллельными поверхности Земного эллипсоида. Поэтому при определении углов рефракции необходимо учитывать и это обстоятельство.
Для больших зенитных расстояний целесообразно получить дифференциальное уравнение рефракции, свободное от этих недостатков. В первую очередь получим выражение, которое позволяло бы определять углы рефракции при любых зенитных расстояниях, включая и 900.
В инварианте Снеллиуса
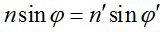 (2)
(2)
примем 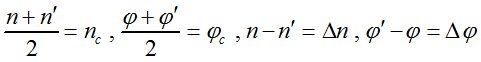 .
.
Тогда
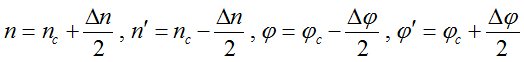 .
.
С учетом этих значений инвариант Снеллиуса примет вид
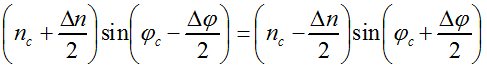 .
.
После преобразований имеем
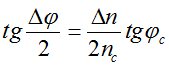 . (3)
. (3)
Полученная формула является строгой и ее можно использовать при любых значениях φ. Учитывая малое значение Δφ, можно принять 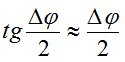 . Тогда, принимая во внимание
. Тогда, принимая во внимание 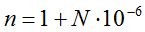 , где N – индекс преломления,
, где N – индекс преломления,
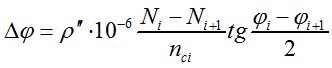 .
.
Угол полной рефракции
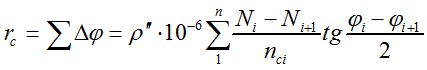 , (4)
, (4)
где 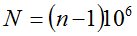 - индекс преломления.
- индекс преломления.
Для определения входящих в формулу (4) углов φi , φi+1 в сферической модели атмосферы используют известный инвариант 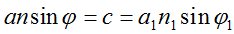 , откуда
, откуда
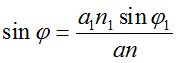 , (5)
, (5)
где а1 – расстояние от центра Земли до начальной точки траектории оптических волн, аi – до текущей точки i; n1, n – коэффициенты преломления в начальной и текущей точках соответственно; φ1 , φ – углы между нормалью к изодиоптрической поверхности и траекторией луча в начальной и текущей точках.
Более строго атмосферные слои целесообразно аппроксимировать эллипсоидами вращения, изодиоптрические слои которых параллельны поверхности Земного эллипсоида, т.е. слои эллипсоидальной атмосферы совпадают с уровенными поверхностями. Для эллипсоидальной атмосферы необходимо учитывать следующее обстоятельство. Радиус кривизны нормального сечения определяют по формуле
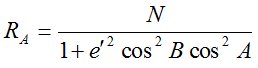 , (6)
, (6)
где радиус кривизны первого вертикала
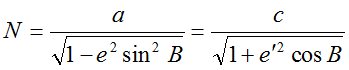 . (7)
. (7)
В формулах (6), (7) е2 и е’2 – квадраты первого и второго эксцентриситетов эллипса; а, с – радиус кривизны экватора и полярный радиус кривизны; В – геодезическая широта; А – азимут нормального сечения.
Значения RA, вычисленные по формуле (6) для различных значений широты В и азимута А, показали, что максимальная разность RA достигает 64,146 км в плоскости меридиана. Выясним, на каком расстоянии от пункта наблюдения оптический луч будет выходить из атмосферы. Известно, что на высоте 30 км в стандартной атмосфере ГОСТ 4401-81 давление р = 1,93 гПа, Т = 226,509 К. На уровне моря р0 = 1013,25 гПа, Т0 = 288,15 К, N0 = 278,24. С учетом этих значений 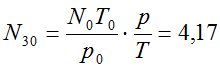 . На высоте 40 км р = 0,287 гПа, Т = 250,350 К, а значение N40 = 0,091.
. На высоте 40 км р = 0,287 гПа, Т = 250,350 К, а значение N40 = 0,091.
Следовательно, на высотах более 30 км атмосфера является разреженной и определение углов рефракции в слое 30 – 100 км можно принимать сферическую модель атмосферы с радиусом кривизны RA на высоте 30 км. Для слоев одинакового коэффициента преломления, параллельных поверхности с изменяющимся радиусом кривизны целесообразно получить формулу, позволяющую определять углы φ между нормалью к этой поверхности и направлением оптического луча. Положим, что для элементарного участка трассы электромагнитных волн атмосфера является сферической. Тогда для участка трассы имеем
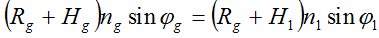 ,
,
для отрезка 1 – 2 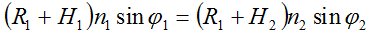 ,
,
для отрезка 2 – А 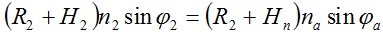 .
.
Подставляя из последнего выражения 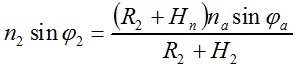 во второе, получим
во второе, получим
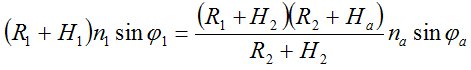 .
.
Подставляя из полученного выражения 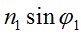 в первое, находим
в первое, находим
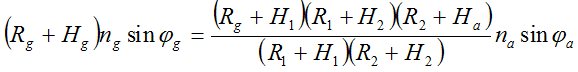 .
.
Или 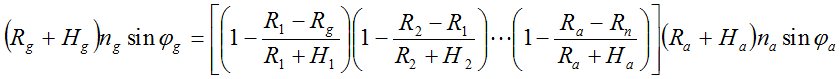 .
.
После небольших преобразований с учетом величин первого порядка малости имеем
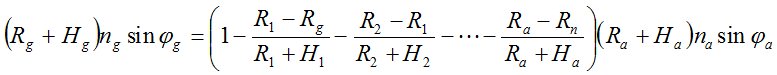 .
.
Учитывая бесконечно малые отрезки трассы электромагнитных волн G – 1, 1 – 2, …,n – A, получим
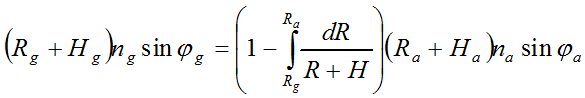 . (8)
. (8)
Используя при интегрировании теорему о среднем значении, находим
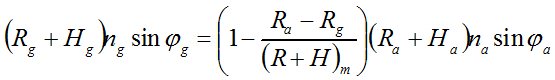 . (9)
. (9)
Значения N для изотермической атмосферы, в которой температура с высотой изменяется по линейному закону, вычисляют по формуле
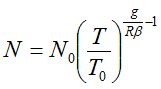 .
.
Сравнение значений rc, вычисленных по формуле (4) для φg = 890 и φg = 900 и условий стандартной атмосферы ГОСТ 4401-81 численным интегрированием с шагом по высоте 0,25 км и путем удвоения шага (0,50 км) показало, что разности значений rc не превышают для φg = 890 0,15”, а для φg = 900 при Н через 0,1 км и для Н через 0,2 км, практически дают одинаковые результаты (разности не превышают 0,07”), что свидетельствует о высокой точности полученной формулы и ее возможности определять углы rc при любых значениях φg, включая и φg = 900. т.е. точность определения углов rc является достаточно высокой.
Литература
-
В.И. Куштин. Учет влияния атмосферы на результаты измерения длин радиоэлектронными системами. Монография. Москва, МИИГАиК, 2003, 179с.
-
Атмосфера стандартная. Параметры ГОСТ 4401-81.-М.: Издательство стандартов, 1981, 280с.