Сравнение результатов вычислений астрономической рефракции вблизи горизонта различными способами

Н.Н. Редичкин; И.Н. Редичкин

Сравнение результатов вычислений астрономической рефракции вблизи горизонта различными способами

Аннотация

Н.Н. Редичкин, И.Н. Редичкин

Выполнены вычисления углов астрономической рефракции различными способами и произведен сравнительный анализ результатов вычислений. Приведены рекомендации по использованию того или иного способа в различных условиях.

Ключевые слова: Астрономическая рефракция, Часовой угол, Зенитное расстояние, Атмосфера, Пулковские таблицы.

25.00.32 - Геодезия

В настоящее время существуют численный и измерительный методы определения углов астрономической рефракции (r_a), каждый из которых имеет несколько способов. Чтобы понять, какой способ эффективнее применять и в каких случаях, необходимо выполнить их сравнительный анализ.

В 1981 году научной экспедицией кафедры инженерной геодезии РГСУ на горе Шитжатмаз вблизи г. Кисловодска были выполнены наблюдения звезды α Vir, и получены следующие данные [1]:

Журнал наблюдений Таблица 1

Дата: 29-30 июля 1981 г.			Звезда: α Vir		α =13^h24^m12,055^s
Пункт: Гаошид			m=1,21		u₁=-19,729^s;
φ =43⁰45^’00^”			N по AE — 326		в T₁=18^h20^m23,0^s
λ=2^h50^m42,25^s			δ=-11⁰03^’47,87^”		ω=-0,144^s.
Инструмент: ОТ-02М №10563; Mz=13,6^”; уровень  контактный
№ п/п	Круг	Отсчеты
		Вертикальный круг 0 ‘ “		Хронометр (х) h m s		t ⁰C	p, мм. рт. ст.
1	L	47,0 91 37 47,4		18 23 30,5		+17,5	597,8
2	L	11,2 91 23 11,6		18 26 28,5		16,8	597,8
3	L	30,2 91 11 29,8		18 28 51,0		16,6	597,8
4	R	40,7 89 03 40,5		18 31 53,5		16,4	597,8
5	R	37,2 89 13 37,6		18 33 58,5		16,2	597,8

После использования этих данных и алгоритма вычислений r_a методом численного интегрирования, приведенного в работе [2], получены результаты, отраженные в табл. 5. Параметры атмосферы в пункте наблюдений приняты по данным работы [2]; в промежуточных точках траектории светового луча на высоте от 3-х до 30км с шагом 1км по данным аэрологического зондирования атмосферы, выполненного на метеостанции г.Минеральные Воды (ближайшая к пункту наблюдений); параметры атмосферы на высотах от 30 до 60 км по таблицам летней модели атмосферы [2].

После использования данных табл. 1 и алгоритма вычислений r_a способом «часового угла» измерительного метода, приведенного в работе [3], получены следующие результаты:

Таблица 2

Вычисление рефракции методом «часового угла»

№ п/п	s	z	ζ	r_a
1	18,38632^h	86⁰ 54’ 49,1^”	86⁰ 44’ 39,2^”	609,9^”
2	18,43576	87 25 20,5	87 13 50,8	689,7
3	18,47534	87 49 50,6	87 37 13,6	757,0
4	18,52603	88 21 18,2	88 07 07,6	850,6
5	18,56076	88 42 54,7	88 27 01,2	953,5

После использования данных табл. 1 и алгоритма вычислений r_a азимутальным способом измерительного метода, приведенного в работе [3], получены следующие результаты:

- - - - Таблица 3

Вычисление рефракции азимутальным способом

Инструмент: ОТ-02М №10563. Дата: 29/30 июня 1981 г.; M_N=+1.7^”; τ=2,5”
№ п/п	Круг	Отсчеты		Вычисления
№ п/п	Круг	Горизонтальный круг 0 ‘ “	Уровень	А	z	ζ	r_a
1	L	38,1 71 28 38,0	13-27	71⁰ 28’ 36,3^”	86⁰ 54’ 40,5^”	86⁰ 44’ 39,2^”	601,3^”
2	L	10,0 72 00 10,1	14-28	72 00 08,3	87 25 27,4	87 13 50,8	696,6
3	L	08,7 72 25 08,3	13-27	72 25 08,6	87 49 58,4	87 37 13,6	764,8
4	R	02,0 107 03 02,1	28-14	72 56 56,3	88 21 23,2	88 07 07,6	855,6
5	R	11,1 106 41 11,3	27-13	73 18 47,1	88 42 03,5	88 27 01,2	962,3

Для данных табл. 1 выполним определения r_a методом «однородной атмосферы» [4] и по Пулковским таблицам рефракции (пятое издание 1985г.). В таблицах этого издания (составлены на основе современных результатов изучения физических и оптических свойств земной атмосферы) сохранена традиционная логарифмическая форма представления рефракции [5].

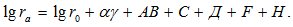(1).

Результаты вычислений r_a по формуле (1) представлены в табл. 4.

Таблица 4

Вычисление рефракции по Пулковским таблицам

е=20 гПа; р=797 гПа; φ=43⁰45’; Н=2056,1 м; Спектр: В₂
№ п/п	ζ	t, ⁰C	lgr₀	λ γ	AB	C	Д	F	H	Lgr_a	r_a
1	84⁰ 44’ 39,2^”	17,5	2,90117	-478	-10627	-291	25	-3	-190	2,78553	610,3
2	87 13 50,8	16,8	2,94693	-360	-10665	-301	25	-4	-232	2,83156	678,5
3	87 37 13,6	16,6	2,98628	-336	-10703	-309	26	-4	-268	2,87034	741,9
4	88 07 07,6	16,4	3,04055	-317	-10763	-334	27	-5	-525	2,92138	834,4
5	88 27 01,2	16,2	3,07936	-289	-10826	-383	28	-6	-1139	2,95321	879,9

Для анализа результатов определений r_a различными способами сделаем сводную таблицу (табл. 5).

Таблица 5

Сравнение результатов вычислений рефракции различными способами

№ п/п	Измеренное зенитное расстояние (звезда α Vir)	Вычисленные значения углов r_a
		Измеренный метод		Расчетный метод
		r_a^А	r_a^t	Численное интегрирование	Однородная атмосфера		Пулковские таблицы
		r_a^А	r_a^t	Численное интегрирование	(1)	(2)	Пулковские таблицы
1	2	3	4	5	6	7	8
1	86⁰ 44’ 39,2”	601,3”	609,9”	619,6”	619,2”	612,4”	610,3”
2	87 13 50,8	696,6	689,7	687,6	687,0	681,5	678,5
3	87 37 13,6	764,8	757,0	752,1	751,3	745,9	741,9
4	88 07 07,6	855,6	850,6	850,8	848,4	843,9	834,4
5	88 27 01,2	962,3	953,5	929,1	927,5	923,5	897,9

Анализируя результаты вычислений r_a , приведенные в табл. 5, можно сделать вывод, что наиболее точным расчетным способом определения r_a является способ решения интеграла рефракции методом численного интегрирования. Этот способ можно использовать для расчетов на ЭВМ, например, при составлении таблиц рефракции по моделям атмосферы или при определении r_a по данным аэрологического зондирования атмосферы.

Наиболее простым способом расчетного метода определения r_a является алгоритм решения с использованием формул для однородной атмосферы. Однако этот способ не является высокоточным, из-за приближенных значений коэффициента k , определяющего высоту преломления.

Углы рефракции, полученные различными способами и приведенные в табл. 5 позволяют считать, что углы r_a^t, полученные измерительным методом, по абсолютной величине в среднем ближе к вычисленным по данным аэрологического зондирования, чем по Пулковским таблицам.

Расчетные способы: численного интегрирования (с использованием данных аэрологического зондирования атмосферы) и однородной атмосферы, практически совпадают до зенитных расстоянийζ=87⁰. На ζ>87⁰ расхождения в пределах ошибок измерений, т.е. ±2-3.

Измерительные способы: азимутальный (r_a^А) и часового угла (r_a^t) не совпадают примерно на 7, независимо от зенитного расстояния, что можно объяснить влиянием неучтенных систематических погрешностей.

Эти выводы позволяют считать, что при выполнении исследований астрономической рефракции на больших зенитных расстояниях углы r_a необходимо определять измерительным методом, а для вычисления аномалий (Δr_a=r_a^изм - r_a^теор) в качестве теоретических значений использовать не Пулковские таблицы, а формулы метода численного интегрирования.

Этот вывод соответствует выводу директора Пулковской обсерватории В.К. Абалакина, сделанному им в предисловии к Пулковским таблицам, где сказано, что «… при экстремальных значениях параметров (например, для наблюдений на большой высоте Н и больших зенитных расстояниях ) Пулковские таблицы рефракции утрачивают свою точность» [5].

Сравнение углов r_a, полученных измерительным методом, с углами, вычисленными по Пулковским таблицам, позволяет считать, что для учета рефракции вблизи горизонта измерительный метод на 1-2 порядка точнее, чем по Пулковским таблицам.

Литература

1. Редичкин И.Н. Вычисление углов астрономической рефракции вблизи горизонта различными способами и сравнение результатов.- В сб.: Прикладная геодезия. Изд-во РГСУ, Ростов-на-Дону, 1999.- с.93-102. Деп. ВИНИТИ 7.04.99 №1058-699.

2. Алексеев А.В., Дробязко Д.Л., Кабанов М.В., Куштин И.Ф. Оптическая рефракция в земной атмосфере (рефракционные модели атмосферы). - Новосибирск: Наука, 1987.- 104с.

3. Куштин И.Ф. Методы определения углов рефракции и поправок в дальность.- В сб.: Геодезия и фотограмметрия, изд. РИСИ, Ростов-на-Дону, 1986.- с.3-15.

4. Куштин И.Ф. Определения углов рефракции методом однородной атмосферы.- В кн.: Рефракция оптических волн в атмосфере (сборник статей).- Томск, 1982.- с.28-43.

5. Таблицы рефракции Пулковской обсерватории.- Л.: Наука, 1985.- 49с.