Задача о статическом внедрении конического индентора в область с радиальными начальными напряжениями
Аннотация
Рассматривается задача о вдавливании конического индентора в предварительно сжатую радиальными усилиями упругопластическую среду. Оценивается влияние начальных напряжений на параметры вдавливания.
Ключевые слова: Диагностика, ресурс, работоспособность, механические характеристики, прочность, пластичность, твердость, вязкость, неразрушающий контроль, разрушающий контроль, метод конечных элементов, ANSYS
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Наиболее важными задачами в строительстве и машиностроении являются: повышение качества зданий, сооружений, машин и механизмов, обеспечение их надежности и работоспособности в течение всего срока эксплуатации. В последние годы участились аварии магистральных нефте- и газопроводов, водоводов, обострилась проблема обеспечения надежности металлоконструкций на предприятиях нефтехимической и энергетической промышленности. Следует также отметить, что после прекращения деятельности многих предприятий, здания и сооружения остались некоторое время без ухода и обслуживания. Особенно этот вопрос актуален в случае реконструкции после неблагоприятных внешних воздействий [ 1, 2, 3].
Основными методами оценки механических характеристик материалов являются разрушающие методы, тем не менее, особенно в последнее время, приобретают популярность неразрушающие методы контроля. Одним из таких методов является известный метод вдавливания инденторов (определение твердости). Если говорить об измерениях непосредственно на объекте, то большой практический интерес представляет оценка влияния напряжений, уже присутствующих в конструкции на параметры вдавливания.
Для оценки этого влияния была решена задача о статическом вдавливании конического индентора в предварительно нагруженное упругопластическое пространство. Для решения этой задачи был использован известный метод конечных элементов (МКЭ). Моделирование производилось с использованием программного продукта ANSYS. Была разработана конечноэлементная модель в осесимметричной постановке (рис. 1, а). Для моделирования полубесконечного пространства использовали четырехузловые изопараметрические четырехугольные элементы, число которых варьировалось от 250 до 1000. Общее число узлов также выбиралось от 300 до 2000. С целью лучшего предсказания реакции материала полупространства, области контакта, распределения контактных напряжений, полей напряжений и деформаций потребовалось более частое разбиение сетки в области контакта. Горизонтальное и вертикальное разбиение в контактной зоне сразу под индентором составляло от 0,02 до 0,05 мм при размерах окончательной зоны контакта не более R=1,5 мм. Для моделирования индентора использовали треугольные шестиузловые элементы. В связи с тем, что в качестве материала инденторов обычно используют либо алмаз, либо твердые сплавы (ВК6, ВК8), при моделировании его свойства были заданы только упругими константами.
Для определения зоны контакта между поверхностью полупространства и коническим индентором применялось несколько десятков контактных элементов типа поверхность-поверхность, причем одна из контактных поверхностей (targe) принадлежит рабочей поверхности индентора, как наиболее твердой, а другая (conta) – поверхности полупространства (рис. 1, а). Такая система применяются для идентификации контакта и разделения узловых точек контактируемых тел во время деформации. Контактный узел, попавший на мишень, может скользить вдоль линии с коэффициентом трения и вызывает силы в нормальном и тангенциальном направлениях.
Если в процессе деформации зазор в контактном элементе оказывается меньше допускаемого значения, то, значит, произошел контакт и прикладывается соответствующее контактное давление в узловых точках.
Для моделирования упругопластических свойств материала полупространства применяли мультилинейную модель с кинематическим упрочнением, при которой нелинейная зависимость между напряжениями и деформацией заменяется кусочно-линейной кривой.
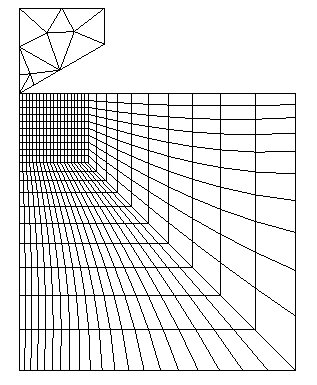
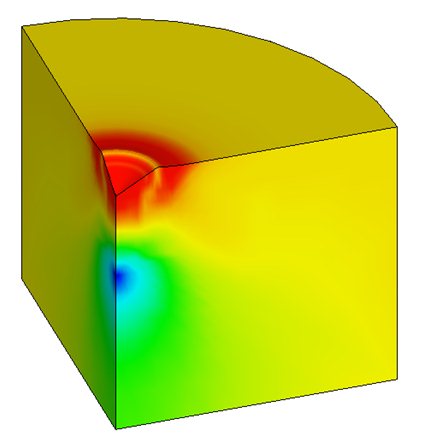

а) б)
Рис. 1. – Сетка конечных элементов и поля эквивалентных напряжений в упругопластической области
Нагрузка при решении задачи была приложена смещением верхних узлов индентора (рис. 1, а). Для улучшения сходимости решения итеративный процесс продолжался до выполнения условия снижения параметра сходимости до значений 10-4 (0,01%). Назначенное вертикальное смещение штампа выбирали из условия выполнения сходимости решения в пределах 5 итераций.
Решение упругопластических задач методом конечных элементов позволяет нам учесть по возможности максимальное количество факторов, оказывающих влияние на процесс вдавливания.
Задачу решали при следующих граничных условиях:
-
все точки упругопластической области с координатой z=-h закреплены в вертикальном направлении (Uz=0), где h – высота упругопластической области;
-
все точки, лежащие на оси симметрии закреплены в радиальном направлении (Ur=0);
-
давление конуса на образец моделировали последовательным смещением верхней части конуса;
-
на удалении R на упругопластическую область действует распределенная нагрузка q, величину которой выбираем в зависимости от требуемой величины начального напряжения.
Условие текучести материала базировалось на критерии Мизеса:
f = J2 – k2=0,
где k - константа материала; J2 - второй инвариант тензора девиатора напряжений (1).
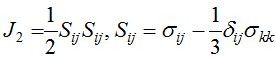 . (1)
. (1)
Если ввести эквивалентные напряжения Мизеса М , то условие текучести может быть представлено в виде:
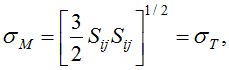
где Т - предел текучести при одноосном растяжении.
В результате решения задачи получили распределение полей смещений, деформаций, напряжений. На рис. 1, а показаны поля эквивалентных напряжений Мизеса (в Паскалях) для уровня начальных напряжений 1,25Т. На рисунке имеется зона разгрузки на глубине примерно 2a по оси симметрии, где a – радиус отпечатка. Такое напряженно-деформированное состояние характеризуется низким уровнем (или полным отсутствием) касательных напряжений и близко к гидростатическому сжатию.
а) б)
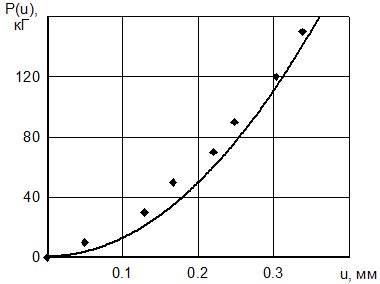
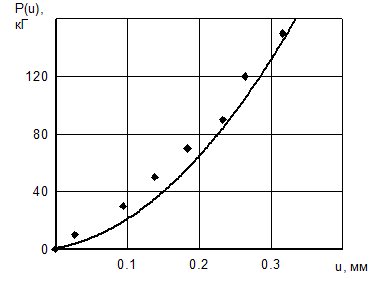
Рис. 2. – Зависимости усилия от углубления для стали 20 и конуса 1200
а) и б) – без преднапряжения и преднапряжения на уровне текучести;
– – МКЭ; • – эксперимент
На рис. 2 представлены зависимости нагрузки на инденторе от глубины его внедрения. На графиках видно, что эксперимент показывает более высокие значения усилия, чем дает моделирование. Это объясняется наличием некоторого радиуса в вершине конического индентора.
Анализ результатов показывает увеличение нагрузки на инденторе при увеличении уровня начальных напряжений. Однако, стоит отметить, что более существенно (около 16% и выше по результатам численного анализа) это увеличение проявляется лишь при уровнях этих напряжений, превышающих предел текучести для рассматриваемого упругопластического материала.
Литература
-
Вернези Н.Л., Веремеенко А.А., Веремеенко Е.Г. Диагностика прочности металлических конструкций. // Новые технологии НБ МГТУ, вып. 4, 2012.
-
В. В. Литвинов, Б. М. Языев, А. Н. Бескопыльный Устойчивость круговой цилиндрической оболочки при равномерном внешнем давлении // Инженерный вестник Дона, вып 4, 2011
-
А. Н. Бескопыльный, М. И. Кадомцев, А. А. Ляпин Методика исследования динамических воздействий на перекрытия пешеходного перехода при проезде транспорта // Инженерный вестник Дона, вып. 4, 2011