Снижение сварочных деформаций тонкостенных панелей теплообменных аппаратов путём регулирования податливости кромок при выполнении круговых швов
Аннотация
Выполнение круговых угловых швов на тонкостенных панелях теплообменных аппаратов вызывает деформации и перемещения, обусловленные потерей устойчивости тонкостенного элемента, что является следствием действия усадочных сил в плоскости пластины. Выполнение отбортовки кромки отверстия панели в месте расположения кругового шва на расчетно-обоснованную величину позволяет увеличить податливость соединяемых кромок и вынести действие усадочных сил из плоскости панели, благодаря чему появилась возможность снизить временные и остаточные деформации тонкостенного элемента до уровня, позволяющего применять для сварки неадаптивные автоматы или роботы.
Ключевые слова: тонкостенная панель, круговой шов, деформация, перемещения, потеря устойчивости, торцовый шов, отбортовка, податливость, роботизация.
Основное направление развития современного машиностроения- это автоматизация производства. Для сварочного производства высшей степенью автоматизации является роботизация. Роботизация изготовления простых и жёстких конструкций, как правило,приводит к получению продукции высокого качества. Однако среди всего многообразия металлоконструкций, изготавливаемых с применением дуговой сварки, особое место занимает большая группа изделий, для которых характерна малая жёсткость и наличие большого количества близко расположенных круговых швов. В работе в качестве примера рассматривается теплообменник – узел бытового газового обогревателя (см. рис.1.). Процесс дуговой сварки указанных конструкций, в силу неравномерности нагрева изделия, сопровождается появлением временных и остаточных деформаций. Это значительно осложняет внедрение неадаптивных роботов и автоматов в сварочное производство маложестких конструкций с близкорасположенными круговыми швами.
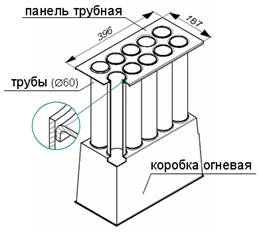
Рис.1. Теплообменник.
При выполнении ручной дуговой или механизированной сварки, временные перемещения, как правило, не осложняют процесса сварки, так как сварщик ориентируется на действительное положение кромок и позиционирование электрода относительно стыка не вызывает затруднений. При сварке конструкций с близким расположением швов, деформации и перемещения, возникающие после выполнения части швов, могут изменять первоначально заданное расположение ещё не сваренных элементов, т.е. приводить к отклонению положения стыка от запрограммированной траектории движения электрода. Поэтому, при сварке с использованием неадаптивных сварочных роботов или автоматов, позиционирование свариваемых кромок и конца электрода для каждого очередного шва требует учёта как временных, так и остаточных перемещений. Это в некоторых случаях ставит под сомнение принципиальную возможность применения неадаптивных роботов для сварки подобных конструкций.
Экспериментально показано [1], что при выполнении круговых швов в тонких панелях образуются деформации в плоскости и из плоскости, а так же потеря устойчивости (рис.2.).

Рис.2. Панель трубная после сварки.
Деформации являются результатом двух одновременно протекающих физических процессов - теплового расширения металла и силового взаимодействия соседних неодинаково нагретых зон. По литературным данным [2, 3] установлено, что после сварки кругового соединения в результате продольной и поперечной усадки сварного шва в шве и зоне пластической деформации возникает усадочная сила, которая действует в плоскости панели (рис.3.а.). Поэтому в шве и около шва действуют напряжения растяжения. За пределами зоны пластических деформаций возникают в радиальном направлении напряжения растяжения, а в тангенциальном напряжения сжатия. Такое состояние приводит к появлению деформаций в плоскости и перемещений из плоскости пластины. Если напряжения сжатия превышают критическое значение sкр, то происходит потеря устойчивости и пластина с круговым швом теряет свою первоначальную плоскую форму.
![]() ,
,
где Е - модуль упругости, m - коэффициент Пуассона, S - толщина пластины, R - радиус шва.
При близком расположении сварных круговых швов происходит наложение полей деформаций и напряжений, что приводит к изменениям формы, практически не поддающимся заранее какому либо расчёту [4].
Выявленные виды сварочных деформаций и перемещений приводят к практической невозможности внедрения неадаптивных роботов в производство маложёстких конструкций содержащих близкорасположенные круговые сварные швы.
В работе высказана гипотеза о возможности регулирования величины деформаций в пластине путём выноса усадочной силы за пределы её плоскости. В связи, с чем предложен и исследован конструктивно-технологический метод снижения сварочных деформаций и перемещений при выполнении круговых швов на тонкостенных панелях. Предложено заменить круговой угловой шов (рис.3.а) на торцовый шов, выполняемый по отбортовке (рис.3.б). Благодаря данному методу конструкция в районе расположения сварного шва становится более податливой. Это уменьшает влияние усадочных сил, возникающих в шве, на тонкостенную панель. При определённой высоте отбортовки сварной круговой шов, имеет возможность уменьшаться в диаметре, практически не влияя на тонкостенную панель, что снижает временные и остаточные деформации панели до уровня, позволяющего применять сварку неадаптивными автоматами или роботами.
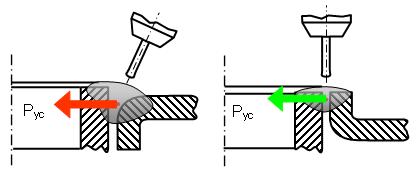
а) б)
Рис.3. Конструктивное оформление кругового шва
а) угловое соединение; б) соединение торцевое по отбортовке
Исследования перемещений в зависимости от конструктивных параметров соединения т.е. высоты отбортовки, диаметра кругового шва и толщины пластины, выполнены МКЭ в программном комплексе АNSYS. На рис.4. представлена расчётная модель соединения «Труба + Пластина». Она строилась, как осесимметричная в плоской постановке, при поведении материала в упругой области. В исследуемой зоне размер сетки конечных элементов сгущался до размера 0,5 мм. Перемещения узлов элементов по линии нижнего торца трубы и углы их поворота равны 0, т.е. моделируется условие жёсткой заделки. Такие же условия накладываются и на свободный край пластины. На внутреннем ободе трубы высотой 2 мм (по глубине проплавления) прикладывали равномерно-распределённую нагрузку, которая является аналогом фиктивной усадочной силы. Величина нагрузки 250 МПа, что по данным [2] соответствует остаточным напряжениям в сварном шве.
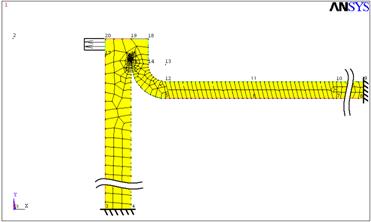
Рис.4. Расчётная модель сварки трубы с пластиной по отбортовке.
Результаты исследований представлены на рис.5. Видно, что с увеличением высоты отбортовки перемещения в плоскости пластины уменьшаются (рис.5.а). Даже при величине отбортовки 3 мм они составляют не более 0,04 мм.
На перемещения из плоскости пластины конструктивные параметры соединения влияют следующим образом:
- с увеличением высоты отбортовки перемещения из плоскости пластины уменьшаются;
- с увеличением толщины пластины перемещения из плоскости пластины уменьшаются;
- с уменьшением диаметра кругового шва перемещения из плоскости пластины уменьшаются.
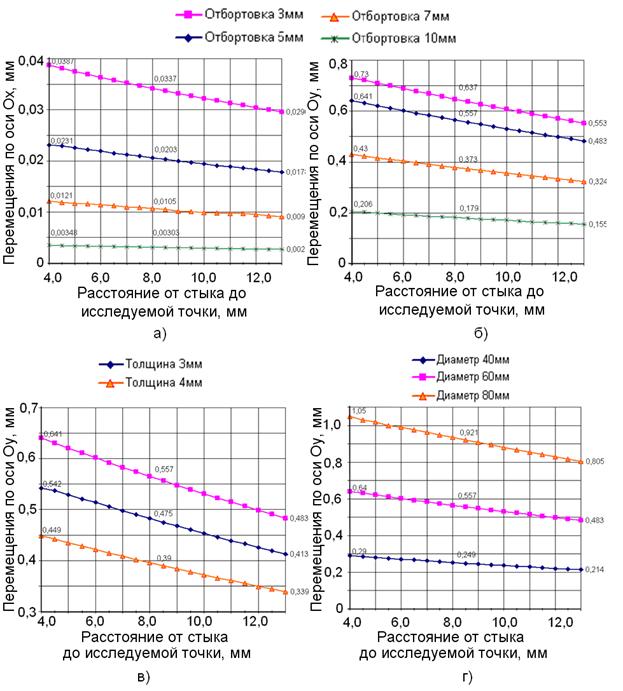
Рис.5. Влияние конструктивных параметров соединения пластины на перемещения узловых точек:
а) влияние высоты отбортовки на перемещения в плоскости;
б) влияние высоты отбортовки на перемещения из плоскости;
в) влияние толщины пластины на перемещения из плоскости;
г) влияние диаметра отверстия на перемещения из плоскости
Оценка МКЭ совместного влияния всех параметров сварного соединения на деформации, возникающие в пластине, при выполнении кругового шва, довольно трудоёмкий процесс т.к. каждый раз необходимо переделывать расчётную модель.
Для определения совместного влияние всех параметров соединения «труба-пластина» на деформации и перемещения был разработан аналитический метод расчёта. Аналитический расчет позволяет находить величину прогиба пластины, в зависимости от совокупного влияния всех конструктивных параметров сварного соединения. При этом с целью упрощения расчета модель принималась осесимметричной и решалась в упругой постановке. Рассматриваемый материал считали однородным, изотропным. Расчётная модель показана на рис.6. Методами строительной механики определялся прогиб, возникающий в пластине. Для чего сварное соединение представлялось в виде модели «короткая оболочка – кольцевая пластина». Теория осесимметричных цилиндрических коротких оболочек, опирается на гипотезы Кирхгофа-Лява:
- гипотеза неизменности нормалей;
- гипотеза о ненадавливании одного слоя на другой.
Указанные гипотезы выполняются достаточно удовлетворительно при условии, что толщина листа мала по сравнению с радиусом цилиндра, что перемещения точек срединной поверхности, малы по сравнению с толщиной.
Введены обозначения:
r1 – радиус цилиндра (оболочки); h1 – толщина стенки цилиндра; h2 – толщина пластины; x – координата, отсчитываемая от торца в направлении оси цилиндра; l – высота цилиндра (оболочки); W – перемещения произвольной точки срединной поверхности (прогиб).; υ =υ (r) – угол поворота нормали срединной поверхности пластины.
Сварное соединение представляется в виде модели «пластина – короткая оболочка» (см. рис.6.).
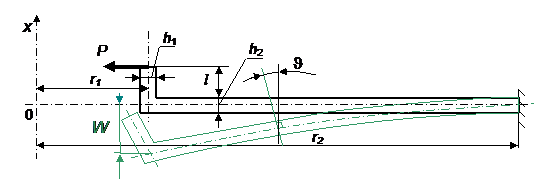
Рис. 6. Модель «Пластина – короткая оболочка»
Механическая постановка задачи: конструкция разбивается на 2 части.
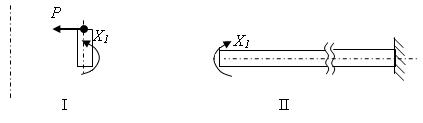
I –Моделирует цилиндрическую оболочку, при этом если bl2 £ 3, то такая
оболочка считается короткой, где 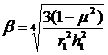 .
.
II – Моделирует кольцевую пластину с отверстием.
Математически эта задача сводится к дифференциальным уравнениям. Составляется уравнения оболочки и пластины, а так же уравнения краевых условий (условия на границе и уравнения совместности деформаций).
Дифференциальное уравнение осесимметричной деформации цилиндрической оболочки согласно строительной механике[5, 6]:
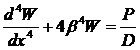 , (1)
, (1)
где W=W(x) - радиальное смещение срединной оси
оболочки, 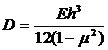 - цилиндрическая жёсткость
- цилиндрическая жёсткость
Граничные условия:
Момент на границе в точке 1: |
|
|
(2) |
|
Приложенная нагрузка в точке 1: |
|
|
(3) |
|
Момент на границе в точке 2: |
|
|
(4) |
|
Перемещения точке 2: |
|
|
(5) |
Получаем математическую постановку из уравнения (1) и граничных условий (2)-(5).
Решение уравнения (1) имеет вид:
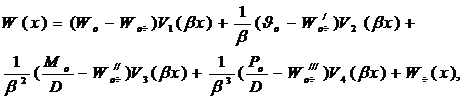 |
(6) |
где: Wo – начальное смещение (при x=0);
υo– начальный угол поворота (при x=0);
Мo– приложенный момент (при x=0);
Po – приложенная фиктивная усадочная сила (при x=0);
V1, V2, V3, V4 – функции Крылова;
Woч, W’oч,W’’oч,W’’’oч– значение частного решения и его производных при х=0.
Далее Wч = 0 т.к. на оболочку не действует распределённое давление р=0, М0 = 0.
Функции Крылова [5] определяются следующими выражениями:
V1(βx)=ch(bx)cos(βx);
V2(βx)=1/2[ch(βx)sin(βx)+sh(βx)cos(βx)];
V3(βx)=1/2sh(βx)sin(βx);
V4(βx)=1/4[ch(βx)sin(βx)-sh(βx)cos(βx)].
Далее рассматривается II участок конструкции – плоский диск с отверстием.
Дифференциальное уравнение пластины [3,4]:
 ® ® |
|
(7) |
Q=0 – поперечная нагрузка в произвольном сечении.
J=J (r) – угол поворота нормали срединной поверхности
P = 0 (Для точки 4)
Решение уравнения (7) имеет вид:
J=с1r+с2/r, (8)
где с1, с2 константы интегрирования.
Граничные условия:
Момент на границе в точке 3: |
|
(9) |
|
Угол поворота нормали в точке 4: |
|
(10) |
где 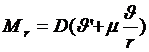 - радиальный момент
- радиальный момент
Условие совместности деформаций: 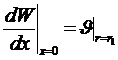 ; (11)
; (11)
Подставляя в условия (2)-(5), (9)-(11) решение (6) и (8) получаем систему пяти уравнений (2), (3), (9), (10), (11) с пятью неизвестными: X1, Р0, J0, с1, с2.
Тогда величина прогиба будет определятся выражением:
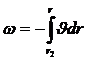 (12).
(12).
С помощью компьютерной программы символьных математических расчётов, выполняется расчёт величины прогиба в зависимости от высоты отбортовки, диаметра шва, толщины пластины и приложенной нагрузки, являющейся аналогом фиктивной усадочной силы P.
В результате решения общий характер полученных перемещений возникающих в пластине оказался такой же, как и при решении МКЭ. На рис. 7. приведено сравнение полученных результатов влияния высоты отбортовки на изгиб возникающий в пластине по МКЭ и предложенном аналитическом расчёте.
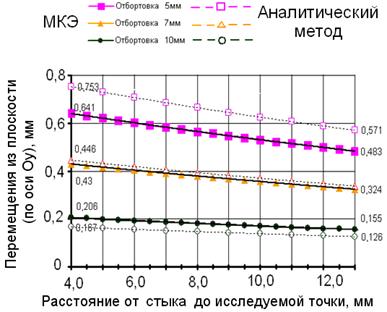
Рис. 7. Влияние высоты отбортовки на перемещения пластины в результате сварки, полученные МКЭ и Аналитическим расчётом.
Таким образом, численным (МКЭ) и аналитическим методами показано, что для уменьшения деформаций пластины в плоскости и из плоскости сварку кругового шва целесообразно выполнять по отбортовке кромок, требуемая высота которой зависит от толщины пластины, диаметра круговых швов, и расстояния между ними.
С увеличением высоты отбортовки и уменьшением диаметра кругового шва, при сохранении расстояния между центрами круговых швов, деформации уменьшаются как в плоскости, так и из плоскости пластины.
С целью подтверждения эффективности предложенного конструктивно-технологического метода была вновь сварена трубная панель, по отбортовке кромок рис.8.
Рис.8. Сварка «трубной панели» торцевым швом
по отбортовке кромок
В результате сварки панель сохранила свою первоначальную плоскую форму. Высказанная гипотеза о возможности предотвращении возникновения сварочных перемещений, деформаций и потери устойчивости путём регулирования податливости сварного шва, за счёт сварки по отбортовке кромок тонкостенной панели получила экспериментальное подтверждение.
Таким образом, разработанный конструктивно-технологический способ выполнения круговых сварных соединений на тонкостенных панелях позволил успешно решить большой комплекс вопросов, связанных не только с уменьшением деформаций и перемещений в зоне круговых швов, но и обеспечил возможность автоматизации сварочного процесса, уменьшения ручного труда, снижения трудоёмкости и повышения качества сварных швов и конструкции в целом.
Список литературы
1. Грицына А.Н. Конструктивно-технологическое проектирование тонкостенных конструкций с учётом их сварки на роботизированных комплексах / А.Н. Грицына, С.В. Тихонов, А.Г. Артёменко // Сварочное производство: сб. тр. молодых учёных/ Изд-во ДГТУ. - г. Ростов н/Д, 2008. – С. 97-103.
2. Винокуров В.А. Сварочные деформации и напряжения / В.А. Винокуров. – М.: Изд-во «Машиностроение», 1968. – 236 с.
3. Неровного В.М. Теория сварочных процессов: учеб. для вузов / В.М. Неровного. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2007. – 752 с.
4. Сагалевич В.М. Методы устранения сварочных напряжений и деформаций / В.М. Сагалевич – М.: Изд-во «Машиностроение», 1974. - 248 с.
5. Бояршиков С.В. Основы строительной механики машин: учеб. для вузов / С.В. Бояршиков. - М.: Изд-во «Машиностроение», 1973. - 456 с.
6. Виноградов С.Н. Конструирование и расчёт элементов тонкостенных сосудов: учеб. пособие / С.Н. Виноградов, К.В. Таранцев. – Пенза: Изд-во Пенз. гос. ун-та, 2004. – 136 с.
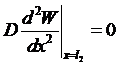

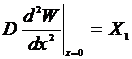
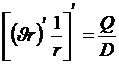 ;
;