Согласование интересов в иерархических системах

Аннотация

Н.К. Жуковская

Рассмотрены особенности согласованного взаимодействия элементов организационной системы (ОС) при наличии  иерархии целей и неопределенности исходной информации. Предложена двухуровневая модель ОС, поясняющая принципы согласования стратегий поведения элементов на основе игрового подхода и нечеткой логики. Первый уровень основан на понятии нечеткой компромиссной игры, позволяющей Исполнителям строить общую стратегию распределения ресурсов между собой на основе переговоров. На втором уровне поставлена задача согласования интересов Центра и Исполнителей на основе равновесных по Нэшу ситуаций.
Ключевые слова: распределение ресурсов, согласование интересов, иерархическая игра, равновесные стратегии, компромисс.

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Введение.
На сегодняшний день используемые методы распределения ресурсов, ориентированные, в основном, на функциональность и рациональность поведения потребителей ресурсов, перестали отвечать современным требованиям к качеству управления. Это определяется, в первую очередь, изменением взглядов на предприятие, которое рассматривается не только как производственная или экономическая система, но и как социальная система. Общим недостатком существующих методов, с точки зрения использования системного подхода к решению задачи распределения ресурсов, является учет отдельных аспектов управления [1, 2].
Упрощенно иерархическую систему рассматривают как совокупность Центра и n Исполнителей. Одной из задач Центра является распределение ресурсов между Исполнителями на основе поступивших от них заявок, а также информации Центра относительно возможности (параметров, характеристик и т.п.) каждого Исполнителя. В настоящей работе рассмотрен подход к распределению ресурсов в организационной системе (ОС) для случая формирования общей заявки Исполнителей на основе следующих положений [3]:
- система существует, когда определена ее цель, объединяющая элементы в единое целое (системообразующий фактор);
- цель конкретной системы установлена системой более высокого уровня;
- элементы ОС активны, т.е. могут выбирать действия, обмениваться информацией;
- каждый элемент ОС имеет собственные интересы;
- игнорирование цели ОС ведет к ее распаду (отсутствие системообразующего фактора);
-  элементы ОС, имея собственные интересы, стремятся в первую очередь реализовать цель системы (это положение приводит к компромиссу интересов).
Из сформулированных положений вытекает следующее:
- Исполнители образуют максимальную коалицию;
- роль Центра по управлению элементами ОС сводится к минимуму;
- с позиции игрового подхода Центр является одним из игроков наряду с другим игроком (максимальной коалицией).
В такой постановке Центр формулирует задачи для каждого Исполнителя, определяет ограничения на ресурсы, требуемые для решения задач, и согласовывает эти ограничения с максимальной коалицией в случае конфликта. Исполнители могут решать задачи на различном уровне качества, преследуя, с одной стороны, свои интересы, с другой — цель ОС. Более высокое качество решения задачи ведет к более высокому стимулированию центром элементов ОС. Стимулирование рассматривается как часть ресурсов ОС. Противоречия интересов Исполнителей, интересов Исполнителя и Центра разрешаются согласованием (компромиссом).
1. Постановка задачи
Представим модель ОС (МОС) представим следующим образом [4]: , где  - Центр,  - Исполнители;  — ресурс, требуемый для решения задачи ;  - множества стратегий элементов ОС;  - целевая функцияi-го Исполнителя, где  - относительное значение возможного ресурса i-го элемента для решения задачи  в ситуации ;  - общий ресурс организации;  - ресурс, выделяемый Центром всем Исполнителям (максимальной коалиции);  - цель ОС;  - предпочтения выбора Исполнителями своих стратегий.
Условие  определяет стремление Центра к минимизации затрат на удовлетворение потребностей ОС при решении задач и максимизации общего ресурса организации (системообразующий фактор). Условие  указывает, с одной стороны, на стремление Исполнителей к удовлетворению своих интересов, с другой стороны — на устремления Центра к максимизации прибыли. И, наконец, условие  является условием существования непустого C-ядра как основы организации максимальной коалиции.
Взаимодействие элементов ОС осуществляется следующим образом. Центр ставит Исполнителям  независимые задачи  и выделяет ограниченный ресурс . Каждый из Исполнителей анализирует возникшую ситуацию, связанную с определением стратегий решения и предпочтением стратегий, исходя из своих интересов и возможностей. В случае возникновения конфликтов Исполнители вынуждены согласовывать свои стратегии поведения, как на основе уступок, так и исходя из соображений сохранения существующей ОС. Разрешение конфликта ведет либо к уступкам какого-то Исполнителя, либо к формированию общей заявки на требуемый ресурс . При появлении новых задач уступки одного Исполнителя могут учитываться другим Исполнителем при согласовании интересов («ты мне — я тебе»); во втором случае (при ) Центр, также заинтересованный в сохранении ОС и решении задач с наилучшим качеством (от этого зависит, например, прибыль), может увеличить  до значения . При получении нового значения  Исполнители решают поставленные задачи, результаты которых оцениваются Центром. Оценка результатов решения задач является основой для стимулирования элементов ОС.
Таким образом, Исполнители, исходя из своих возможностей по выполнению задачи, и наличия ограниченных ресурсов, согласовывают стратегии решения задач, определяют объемы ресурсов (достаточные для решения конкретной задачи) и формируют общую заявку на ресурсы. Заявка может быть принята, либо отклонена Центром. Целью Центра является получение суммарной прибыли, которая увеличила бы ресурсы организации. Целями исполнителей является получение максимальной личной прибыли в условиях ограничений на ресурсы.
В игровой постановке, описанная ситуация, может быть представлена двумя уровнями:
1) иерархической игрой с двумя игроками – Центром, делающим нечетные ходы, и коалицией Исполнителей, использующих четные ходы;
2) игрой Исполнителей, образующих максимальную коалицию и стремящихся  на основе переговоров согласовать свои интересы с целями организационной системы.
3. Иерархическая игра двух лиц «Центр – Исполнители»
Пусть задана игра , где , - конечные множества стратегий Центра и коалиции Исполнителей, G и J  - функции выигрышей игроков (Центра и исполнителей). Здесь  - упорядоченное множество ресурсов, которые Центр может предложить Исполнителям, с заданной выпуклой функцией предпочтения , причем , ;  - задачи, которые необходимо решить независимо n Исполнителям;  - множество ресурсов Исполнителей, которые они могут предложить Центру в качестве альтернативы R;  - стратегии Исполнителей. Целью первого игрока является выбор такого , при данном Z, чтобы в ситуации () его выигрыш  принял возможно большее значение. Целью второго игрока является максимизация выигрыша .
Игра протекает следующим образом. На первом ходе 1-й игрок, в соответствии с функцией предпочтения, выбирает значения ресурсов , достаточные, по его мнению, для решения задач Z, вторым игроком. Задачи Z, а также значения сообщаются второму игроку. В ответ 2-й игрок формирует подмножество стратегий , соответствующих его равновесным ситуациям, и выбирает стратегию . Как отмечалось ранее, при дефиците , реализация  возможна при назначении ресурсов, равных . Поэтому 2-й игрок, на втором ходе игры, информирует 1-го игрока о стратегии  и значении . Несмотря на то, что стратегия 2-го игрока зависит от стратегии Центра, который принимает окончательное решение, на первых ходах имеется высокая неопределенность в игре. Центр, с одной стороны, точно не знает, сколько необходимо ресурсов для решения всех задач, а с другой, может преследовать стратегические цели ОС, стремясь не завышать значение . Исполнители, с одной стороны, могут предполагать блеф Центра, с другой, руководствуясь общей целью ОС, не должны рисковать, слишком отклоняясь от . С такой точкой зрения, окончательной значение выделяемого ресурса, должно быть согласовано между Центром и Исполнителями. Иными словами, при некотором фиксированном значении , функции выигрышей и должны удовлетворить обе стороны. Такое согласование возможно при существовании ситуации , равновесной по Нэшу, т.е. , . Исходя из постановки задачи, выигрыши игроков можно трактовать как полученные прибыли, и определять следующим образом: ; , где  - прибыль, полученная в результате реализации i-й задачи i-м Исполнителем.
Очевидно, что при измерении , ,  в одной шкале, рассматриваемая игра разрешима, если  при .
3. Согласование интересов Исполнителей на основе компромиссной игры
Рассмотрим формальную модель согласования Исполнителями стратегий поведения. Для простоты рассуждений рассмотрим один вид ресурса и двух Исполнителей, которых в дальнейшем будем называть элементами ОС. Пусть  – множества стратегий элементов  и , соответственно, причем ,  . На множествах стратегий заданы нечеткие функции предпочтения . Обозначим через  и  – распределения требуемых ресурсов при использовании соответствующих стратегий, для решения задач  и . Пусть элементам  и  неизвестны предпочтения Центра по удовлетворению их заявок на требуемые ресурсы. В этом случае каждый из них полагает, что он для Центра менее предпочтительный элемент. Введем функцию вида . Данная функция определяет относительные значения ресурсов i-го элемента в ситуации в предположении предпочтения Центром j-го элемента при распределении ресурсов. Значения указывают на недостаток ресурсов в ситуации , а значения на достаточность, либо избыток. На множествах значений  зададим функции  следующим образом [5]:

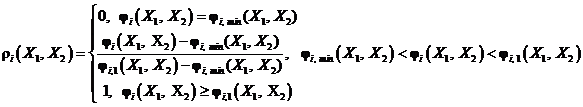
где .
Функция  определяет относительную достаточность ресурсов i-го элемента в ситуации для решения задачи с соответствующим качеством.
Кроме того, на множествах значений каждый элемент  задает нечеткие цели  [5]:
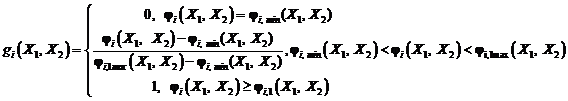      (1)
или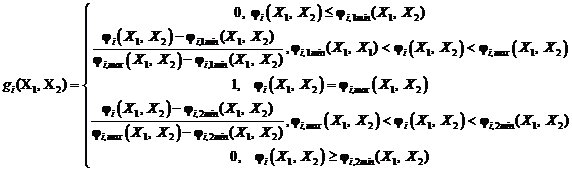
,
где   – наиболее предпочитаемое значение ресурса,  - наименее предпочитаемое значение ресурса среди всех значений больших чем .
Определим область возможных стратегий  в , каждого элемента, с функциями принадлежности вида [6]:
.        (2)
Очевидно, что не все стратегии в  соответствуют предпочтениям элементов ОС. Для отсечения стратегий из  с низкими значениями функции принадлежности  
введем число  и сформируем множество допустимых стратегий  в  следующим образом:
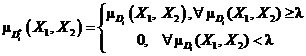
Чем ближе λ к единице, тем меньше вариантов выбора из множества допустимых стратегий, однако эти стратегии будут характеризоваться высокими оценками с точки зрения предпочтения своих стратегий i-м элементом. Для того, чтобы учесть при выборе допустимых стратегий, стратегии других элементов введем множество равновесных стратегий с функцией принадлежности: .
Среди множества равновесных стратегий каждого элемента можно выделить наилучшую равновесную стратегию как . В результате, имеем набор оптимальных, относительно интересов каждого элемента, ситуаций , причем , а .
Ситуация  называется абсолютным компромиссом, если .
Назовем ситуацию  относительным компромиссом, если
 и .
Назовем ситуацию  нулевым компромиссом, если .
Абсолютный компромисс достигается в том случае, если выбор стратегии одного элемента в предположении предпочтения выбора стратегии другого элемента, совпал с предположением, и наоборот. Относительный компромисс возможен тогда, когда в предпочтительной ситуации для одного элемента, использование стратегии другого элемента, изменяющей эту ситуацию, ничего ему не дает, либо усугубляет его положение. В ситуации нулевого компромисса соглашение между элементами ОС невозможно.
4. Пример
Пусть , , . Известны предпочтения выбора элементами своих стратегий: . Кроме того, известно распределение требуемых ресурсов в зависимости от используемых стратегий: , .
Вычислим относительные ресурсы каждого элемента ОС, в зависимости от возможных ситуаций. В результате будем иметь: , , , , , , , .
Определим достаточность ресурсов каждого элемента в ситуации , приняв ==0, =1.16, =1.0. В результате получим: , .
Зададим нечеткие цели  по формуле (1), приняв =0.85, =0.8:
, .
Определим область возможных стратегий  в , каждого элемента, вычислив функции принадлежности по формуле (2): , . Для  сформируем множество допустимых стратегий  в  с функциями принадлежности  : , .
Определим множество равновесных стратегий  с функциями принадлежности : , .
В соответствии с определением ситуация  является относительным компромиссом. Какие обстоятельства должны убедить x1 использовать стратегию ? С одной стороны, стратегия , хотя и относится к множеству равновесных стратегий и соответствует интересам первого элемента, не приводит к компромиссу. Игнорирование этого факта означает неоднозначность поведения, как другого элемента, так и Центра. С другой стороны, кроме преследования собственных интересов, каждый элемент, учитывает цель ОС, которая, в конечном итоге сводится к максимизации ресурсов. В этой связи разные рациональные стратегии приводят к различным значениям . Поэтому, анализируя свои стратегии, первый элемент, должен дать им оценку, с точки зрения возможных значений .
Оценим возможные значения , используя подход, предложенный в [4]. Пусть  – нечеткое множество возможных значений , при условии, что i-й элемент более предпочитаем Центром при удовлетворении заявок на требуемые ресурсы. Тогда, для рассматриваемого случая, функция принадлежности возможных значений ресурсов требуемых каждому элементу , в зависимости от используемых стратегий, имеет вид: .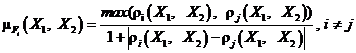
Так, для равновесных стратегий , , , , рассмотренного примера, нечеткие оценки значений ресурсов будут следующими: =0.76,  =0.46, =0.72.
Как следует из данных оценок, использование первым игроком стратегии  при стратегии  второго игрока значительно увеличивает , и как следствие, в случае удовлетворения заявки Центра, уменьшает  в сравнении с ситуацией .
Заключение.
Модель поведения ОС в виде нечеткой иерархической игры определяет принципы взаимодействия элементов на уровне гомеостазиса системы и при наличии у них собственных интересов. Данная модель распадается на две частные модели: модели согласованного взаимодействия n субъектов и модели согласованного взаимодействия Центра и коалиции Исполнителей. Если, до появления задач, сформулированных центром, элементы ОС являются независимыми и пассивными, то после предъявления задач формируются функциональные подсистемы (активные элементы) на основе согласования поведения всех элементов ОС. Иерархическая теоретико-игровая модель согласованного поведения представляется адекватной формализацией проблемы устойчивого развития современных иерархических систем. Предложенный подход допускает развитие для более широкого класса объектов управления. Большой интерес представляет исследование динамической версии модели с различными вариантами информированности игроков.

Литература
1. Опойцев В.И. Равновесие и устойчивость в моделях коллективного поведения. М: Наука. 1977.
2. Васин А.А. Эволюционная теория игр и экономика. Часть I. Принципы оптимальности и модели динамики поведения/Журнал Новой экономической ассоциации, №3-4, 2009.-С.10-27.
3. Астанин С.В., Жуковская Н.К. Анализ подходов к моделированию поведения организационных систем/Изв.ЮФУ. Технические науки, Интеллектуальные САПР, №4, 2008-С.136-141.
4. Астанин С.В., Жуковская Н.К. Конфликтно-игровой подход к распределению ресурсов в организационной системе//Прикладная информатика, №4(34), 2011-С.125-132.
5. Fu A., Wong M., Sze S., Wong W., Yu W. Finding fuzzy sets for the mining of fuzzy association rules for numerical attributes//In Proceedings of the First International Symposium on Intelligent Data Engineering and Learning (IDEAL'98), 1998, pp.263-268.
6. Астанин С.В. Правдоподобные рассуждения в системах принятия рещений.-Таганрог:ТРТУ, Ч2., 2000.-110с.