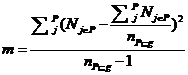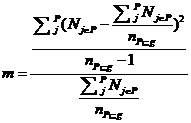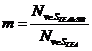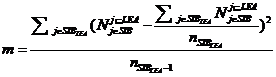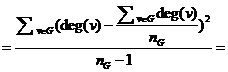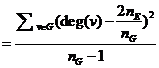Интегрированный алгоритм когнитивной оценки и выбора оптимального варианта онтологической модели
Аннотация
В статье описывается алгоритм, служащий для оценки когнитивных свойств онтологических моделей и последующего выбора оптимального варианта модели из нескольких доступных альтернатив. Авторами предлагается демонстрационная программная реализация алгоритма, выполненная на языке программирования Java.
Ключевые слова: алгоритм, оценка, онтологическое моделирование, многокритериальный выбор, программирование.05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
Процесс когнитивной оценки онтологий можно разделить на два этапа: использование инструментов оценки и принятие решения на основании полученных результатов. Несмотря на развитую теоретическую и прикладную базы этой области знаний, программные реализации алгоритмов оценки пребывают в зачаточном состоянии, и все имеющиеся в открытом доступе программы нацелены только на реализацию первого этапа – использование инструментов оценки, тогда как принятие окончательного решения остается на усмотрение эксперта [1].
Авторами предлагается алгоритм, объединяющий реализацию обоих этапов процесса когнитивной оценки онтологий. В качестве инструмента оценки был выбран расчет метрик, позволяющий оценить когнитивные качества онтологии посредством анализа ее графа. Для поддержки принятия окончательного решения могут быть использованы методы решения задач многокритериального выбора.
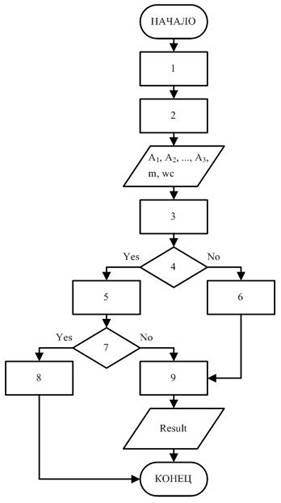
Рис. 1 – Алгоритм когнитивной оценки и выбора оптимального варианта онтологической модели.
Исходными данными для алгоритма являются:
- Набор альтернативных онтологий A1, A2, …, An(для полной реализации алгоритма необходимо минимум две онтологии);
- Метрики m, которые будут использованы при оценке онтологий;
- Весовые коэффициенты wc, сопоставленные метрикам.
- Эксперт (группа экспертов) выбирает метрики m, которые будут использованы при решении задачи.
- Эксперт (группа экспертов) присваивает группе метрик, или каждой из них по отдельности, свой весовой коэффициент wc. Это делается с учетом специфики онтологических моделей, подлежащих анализу. (Например, если у всех рассматриваемых онтологий одинаково высокая ветвистость, весовой коэффициент метрик, связанных с этой характеристикой, может иметь небольшое значение)
- Производится вычисление метрик.
- Выполняется анализ полученных значений. В зависимости от того выходят ли какие-либо метрики за установленные для них пределы значений (например, превышено число Ингве-Миллера для соответствующего семейства метрик), принимается решение о дальнейших действиях.
- Если в пункте 4 были выявлены нежелательные значения метрик, эксперт рассматривает вопрос об исключении из анализа тех онтологий, в которых они были обнаружены.
- Если в пункте 4 нежелательных значений выявлено не было, алгоритм переходит к пункту 9.
- Эксперт принимает решение об исключении из анализа тех онтологий, в которых были обнаружены нежелательные значения метрик.
- Если эксперт решает исключить проблемные онтологии, и после этого остается менее двух альтернатив, выполнение алгоритма прерывается.
- Если количество альтернатив остается достаточным для продолжения выполнения алгоритма, решается задача многокритериального выбора и эксперт получает результат.
Для демонстрации алгоритма авторами была разработана программа MetInt (Metric Interpreter). Текущая версия – 0.9а, реализована в виде Java-приложения с оконным пользовательским интерфейсом. Окно программы показано на рис. 2. Непосредственный расчет метрик производится с помощью инструмента COAT, разработанного при сотрудничестве специалистов Санкт-Петербургского государственного университета, Санкт-Петербургского государственного политехнического университета и Белорусского государственного университета информатики и радиоэлектроники [2]. Инструмент COAT выполнен в виде консольного Java-приложения, осуществляющего вывод вычислений в текстовом виде [3].
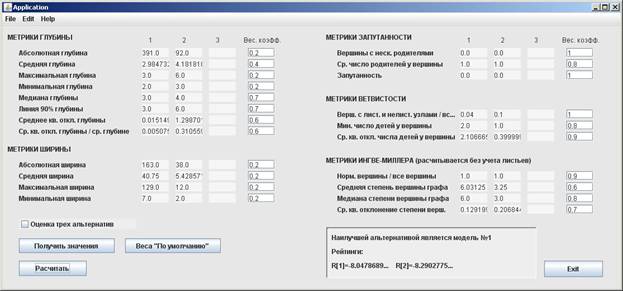
Рис. 2 – Окно программы MetInt v0.9a.
MetInt v0.9a считывает результаты расчетов метрик из текстовых файлов, сгенерированных COAT, после чего позволяет сопоставить каждой из предусмотренных в текущей реализации метрик свой весовой коэффициент. В программе использована часть метрик, описанных в работе [4]. Их подробное описание приведено в таблице 1. Для решения задачи выбора применяется алгоритм, расчитывающий рейтинги альтернатив с использованием нормирующих коэффициентов по формуле (1.1) 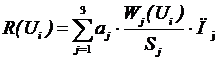 , (1.1)
, (1.1)
где
R(Ui) – рассчитываемый рейтинг i-ой альтернативы;
aj– весовой коэффициент j-го критерия;
Wj (Ui) – значение j-гокритерия оценки для i-ой альтернативы;
Sj – нормирующий коэффициент j-гокритерия, численно равный максимальному значению критерия среди рассматриваемых альтернатив;
Пj– признак. Если j-й критерий стремится к максимуму, то он равен 1, если к минимуму, то -1.
При установке значений весовых коэффициентов стоит помнить, что метрики, характеризующие явные черты структуры графа (максимальная глубина, ширина, и т.п.), дают только самое базовое представление о когнитивных свойствах, тогда как метрики, характеризующие более сложные взаимосвязи, включая статистические, более показательны. В связи с этим, базовым метрикам следует выставлять меньшие значения весовых коэффициентов, а более комплексным – большие. В MetInt предусматривается установка весовых коэффициентов «по умолчанию», однако на практике задача будет иметь более адекватное решение, если эти значения будут установлены экспертом самостоятельно, с учетом специфики рассматриваемых онтологических моделей. Так, если заведомо известно, что модель А обладает большей глубиной чем модель В, но при этом является более полной, значения весовых коэффициентов метрик глубины должны быть уменьшены.
Таблица 1 – Метрики когнитивной оценки онтологических моделей
п/п № |
Группа |
Название |
Описание / алгоритм вычисления |
Комментарии и рекомендации |
|
1.1 |
Метрики глубины |
Абсолютная глубина |
Сумма длин всех путей графа (т.е. путей от корневой вершины к листу) |
Относится к рекомендуемому минимуму. Более предпочтительны небольшие значения данных метрик. |
|
1.2 |
Средняя глубина |
Абсолютная глубина деленная на количество путей в графе | ||
|
1.3 |
Максимальная глубина |
Максимальная длина пути | ||
|
1.4 |
Минимальная глубина |
m = Nj∈P |
Дополнительные метрики оценки глубины онтологии. | |
|
1.5 |
Медиана глубины |
| ||
|
1.6 |
Линия 90% глубины |
Пороговое значение, ниже которого находится 90% значений глубины. Служит для исключения из рассмотрения «выбросов» - т.е. аномально высоких значений. | ||
|
1.7 |
Среднее квадратичное отклонение глубины |
| ||
|
1.8 |
Среднее квадратичное отклонение глубины по отношению к средней глубине |
| ||
|
2.1 |
Метрики ширины |
Абсолютная ширина |
Сумма количества вершин для каждого уровня иерархии по всем уровням |
Относится к рекомендуемому минимуму. Более предпочтительны небольшие значения данных метрик. |
|
2.2 |
Средняя ширина |
Абсолютная ширина деленная на количество уровней иерархии | ||
|
2.3 |
Максимальная ширина |
Количество вершин на уровне, с наибольшим количеством вершин. | ||
|
2.4 |
Минимальная ширина |
Количество вершин на уровне, с наименьшим количеством вершин. | ||
|
3.1 |
Метрики запутанности |
Вершины с несколькими родителями |
Количество вершин, имеющих более одного родителя. |
Множественное наследование в большинстве случаев нежелательно. Однако, если его использование неизбежно, то более предпочтительны небольшие значения данных метрик. |
|
3.2 |
Среднее количество родительских вершин у вершины графа |
| ||
|
3.3 |
Запутанность онтологии |
| ||
|
4.1 |
Метрики ветвистости |
Количество вершин, у которых есть и листья, и нелистовые ноды в качестве детей, по |
|
Характеризуют «распределение» вершин графа, в котором рассматриваются только дуги отношения is-a (или любое другое, являющееся основным в онтологии). |
|
4.2 |
Минимальное количество детей-листьев у предпоследних вершин в графе. |
| ||
|
4.3 |
Среднее квадратичное отклонение детей-листьев у предпоследних вершин в графе. |
| ||
|
5.1 |
Метрики Ингве-Миллера |
Отношение количества вершин с нормальной степенью ко всем |
|
Число Ингве-Миллера, равное |
|
5.2 |
Средняя степень вершины графа |
| ||
|
5.3 |
Медиана степени вершины графа |
| ||
|
5.4 |
Среднее квадратичное отклонение степени вершины графа |
|
На данный момент характеристики программы включают:
- поддержку 22 метрик (метрики фиксированы, но в случае необходимости часть из них может быть исключена из анализа путем установки нулевого весового коэффициента в соответствующем поле);
- возможность сравнения двух или трех онтологических моделей;
- вывод результата в окне программы как в виде рекомендации, так и в виде непосредственных значений рейтингов альтернатив.
Литература:
1. Мохов В.А., Сильнягин Н.Н. Анализ перспектив программной оценки когнитивных свойств онтологий // Моделирование. Теория, методы и средства : материалы XI Междунар. науч.-практ. конф., г. Новочеркасск, 31 марта 2011 г. / Юж.-Рос. гос. техн. ун-т (НПИ) - Новочеркасск : ЮРГТУ, 2011. - С. 158-163.
2. Субъективные метрики оценки онтологий. Гаврилова Т.А., Горовой В.А., Болотникова Е.С., Горелов, В.В. Знания-Онтологии-Теории (ЗОНТ-09), 2009
3. COAT Google Code web page. http://code.google.com/p/ontoeval/downloads/list
4. Gangemi A., Catenacci C., Ciaramita M., Lehmann J. Ontology evaluation and validation. An integrated formal model for the quality diagnostic task. http://www.loa-cnr.it/Files/OntoEval4OntoDev_Final.pdf