Pareto-Based Approach to the Optimization of Schedule for the Polymeric Composite Structures Cure Process
Аннотация
Дата поступления статьи: 04.12.2013Resin transfer molding is a widely used composite material manufacturing process that produces high-strength and lightweight parts for various industrial applications. In order to manufacture defect-free parts with consistent material properties, it is important to control process parameters throughout the entire volume of the molded part. Usually a curing schedule includes a pre-warming to the resin viscosity reaches a minimum, further applying of pressure, and finally consolidation of resin at elevated temperature to its full polymerization. To ensure the uniformly state of the composites across the thick-walled products, we propose a model-based approach to the problem of optimal control synthesis using a mathematical model for curing an epoxy-based composite structure with varied thickness. The PDE system linking a kinetic equation with heat transfer equation takes into account an exothermic heat, a phase transition of resin from liquid to gel and further to the solid state, and well describes the cure process which is controlled by independent heat sources. To synthesize the multi-objective optimal control law, we perform the transient analysis of the developed model to calculate the coordinates of Pareto points in the 8-dimensional space of design variables. An efficiency of such approach in the manufacturing applications we demonstrate on example of cured glass-epoxy composite part with a varied thickness.
Ключевые слова: Composite material; Curing process; Optimal control; Kinetic equations; PDEs in connection with control and optimization, Finite element modeling – FEM, Pareto frontier
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Introduction
High performance polymeric composites are increasingly used in aircraft and ship structures due to its good strength, elastic properties, corrosion resistance, and durability. Resin transfer molding is a popular manufacturing process for composite materials because of its ability to manufacture complex-shaped parts with high efficiency and low pollution. This process begins by the placing of a pre-weighted amount of premixed compound in a heated mould. As the mould closed and heated, the resin matrix material flows and fills the mould cavity and the fine crevasses between the fibers in a composite part. The application of pressure and elevated temperature causes the raw prepreg material to make the desired shape, defined by geometry of the mould. Pressure is applied when the mould is in a closed position. At the first stage of curing the resin viscosity reaches a minimum, caused by outside heat and the heat of reaction of the functional groups, and then increases rapidly due to molecular chain extension. The next step in the reaction is gelation - when the chains start to cross-link, the resin no longer flows and most individual reaction rates decrease markedly. The third step at high cross-linking is vitrification [1 - 3].
The mould is heated by the set of electric elements, and their temperature is monitored and controlled by the automatic control loop [1, 2]. Heat-up rates, cool-down rates, and applied pressure are controlled together to ensure even curing throughout the part and to reduce the possibility of residual stresses causing structural deficiencies or distortions [1, 3-5]. The need for complex heating/pressure cycles is necessary to accommodate the requirements of the chemical reactions and to ensure that the resin viscosity is optimum when pressure is increased. So, because the viscosity of the resin falls with increasing temperature until the resin begins to chemically cross-link (gel), it is important that pressure is applied before gelation occurs to allow removal of entrapped gases and removal of excess resin. This would avoid the severe porosity and resin-rich areas.
To reduce the cure time, sometimes an increasing the cure temperature or using a preheating of resin by some manners, which provide faster crosslinking reactions, are used [6]. But this can lead to significant loss of the composite product quality, which appears in the forms of large shape distortions and delaminations. In general, residual stresses and shape distortions will increase with increased cure temperature [2, 3, 4]. To avoid this problem in the some cases gelled the resin at low temperature and slowly increased the temperature by a linear ramp up to its maximal value [1, 2, 7]. The temperature-time law usually incorporates the dwell sections (isothermal hold) to prolong the time for consolidation and volatile removal. This hold also pre-reacts the resin and reduces the danger of intensive exothermic reactions that can occur in thick laminates [3], and also allow the temperature to become more uniform; this is very important in components with large variations in thickness.
The main difficult in the large composite parts manufacturing is unobservability of the state of material during cure process. The known methods including Differential Scanning Calorimetry, Raman Spectroscopy, and Dielectric Analysis can be effectively used at the laboratory conditions only [8]. Therefore, a model-based control strategy used here assumes the formulation a mathematical model of the controlled cure process, that allow an access both the observed and the hidden parameters of the process, and to build the control law [9, 10].
The presented model of the epoxy based composites curing incorporates the kinetics of the thermoset resin reactions, changing its phase state, thermal capacitance during cure, heat transfer in the whole technological system and multi-input control of the heaters. On the basis of this model we formulate and solve the problem of synthesis optimal temperature schedule using the Pareto frontier approach. This approach is a very efficient at the cases where process quality is characterized by the two or more objectives. Most often, these objectives are not equal in importance and difficulty of achieving them. This inequivalence may be due to strong technical constraint on the controllable parameters (design variables) and also by the self nature of the controlled plant. At the most often used approach when one objective is constructed and incorporates all quality criteria [11], it is difficult to determine a weight of each objective and to estimate a possibility of achieving their optimal value. Moreover, for the complex process the optimal solution is not a unique point, but a set of the feasible points in a multidimensional space of quality criteria.
The Kinetics Equation of Studied Epoxy Resin Cure
First description of the cure process given by the kinetic equation is applied by Kamal [12] for epoxy resin and used with some extensions in many works, e.g. [13 - 16]. The primary depending variable whose behavior is described by a kinetics equation is degree of cure (i.e. conversion) which is defined as an amount of evolved heat during the exothermic reaction ![]() , where
, where ![]() are an actual and the total heat during the polymerization of unit mass, respectively [12, 13]. For some kinds of thermoset plastics, different forms of kinetic equations have been proposed and derived using Differential Scanning Calorimetry - DSC (see e.g. [14-17]), but these forms of equations are not satisfactory due the two-modal dependencies
are an actual and the total heat during the polymerization of unit mass, respectively [12, 13]. For some kinds of thermoset plastics, different forms of kinetic equations have been proposed and derived using Differential Scanning Calorimetry - DSC (see e.g. [14-17]), but these forms of equations are not satisfactory due the two-modal dependencies ![]() (see Fig. 1) that have been reconstructed from the DSC scanning data.
(see Fig. 1) that have been reconstructed from the DSC scanning data.
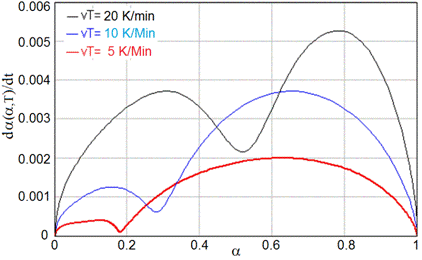
Fig. 1. Kinetics curves for three different heating rates
To describe such kinetics dependencies a new kinetic model and empirical dependence for heat capacity ![]() have been proposed [18]
have been proposed [18]
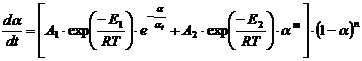 (1)
(1)
![]() , (2)
, (2)
where ![]() are the kinetic model parameters defined by smoothing the kinetic curve;
are the kinetic model parameters defined by smoothing the kinetic curve; ![]() and
and ![]() are the specific heats of uncured (liquid) and fully polymerized (solid) resin respectively; conversion
are the specific heats of uncured (liquid) and fully polymerized (solid) resin respectively; conversion ![]() corresponds to the jump of heat capacity at the phase transition; and the width of the jump in the smoothed Heaviside function
corresponds to the jump of heat capacity at the phase transition; and the width of the jump in the smoothed Heaviside function ![]() for the studied resin have defined by these empirical relationships
for the studied resin have defined by these empirical relationships ![]() ;
; ![]() .
.
Equation (2) describes the jump of the heat capacity at the phase transition, and “broadening" of this jump with increasing heating rate. Relationship for the dependency of resin thermal conductivity is similar to (Eq. 2) can be obtained after a replacement ![]()
![]()
![]() . Both empirical dependencies for the specific heat and thermal conductivity on the degree of cure are shown in Fig. 2.
. Both empirical dependencies for the specific heat and thermal conductivity on the degree of cure are shown in Fig. 2.
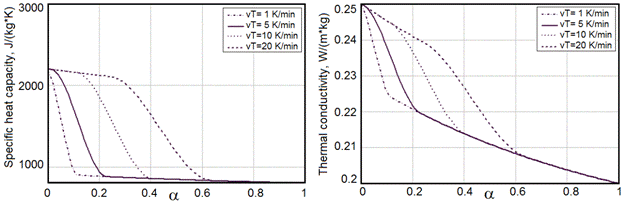
Fig. 2. The dependencies of specific heat capacitance (left) and thermal conductivity (right) on the conversion at different heating rate
Coupled Cure Kinetics and Heat Transfer in a Closed Mould Cure Process
When a cured part occupy some closed volume in a heated mould the temperature and rheological state of composite material will changed in the different points of material. Hence, temperature field and conversion field changing over time, influencing each other and a heat transfer is strongly coupled with propagation of ![]() . The similar problem has been considered in [18-21] at a few simplified statement. In this article we consider this coupled problem on an example of a composite spar for the helicopter tail rotor blade. The problem statement for the cured composite body includes the heat transfer equation
. The similar problem has been considered in [18-21] at a few simplified statement. In this article we consider this coupled problem on an example of a composite spar for the helicopter tail rotor blade. The problem statement for the cured composite body includes the heat transfer equation
![]() , (3)
, (3)
where density of composite material is defined through the densities of resin ![]() , density of the reinforcing fibers
, density of the reinforcing fibers ![]() , and relative quantity of fibers
, and relative quantity of fibers ![]() according to the mixing rule [20]
according to the mixing rule [20]
![]() , (4)
, (4)
the heat transfer coefficient of filled composite [19, 20]
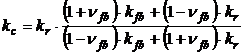 .(5)
.(5)
In the last equation an actual value of heat transfer coefficient ![]() for the resin matrix is defined by a function of conversion
for the resin matrix is defined by a function of conversion
![]() (6)
(6)
The specific thermal capacity ![]() of composite in equation (3) is also defined by the mixing rule
of composite in equation (3) is also defined by the mixing rule
![]() (6)
(6)
Heat transfer equation (3) is coupled with the kinetics equation (1) for conversion ![]() which is a function of space coordinates, temperature, and time.
which is a function of space coordinates, temperature, and time.
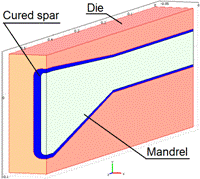
All above equations are active in the spar body only, and the heat transfer equation (3) with appropriate coefficients is active everywhere. All boundary conditions depend on the cured piece and mould geometry (see Fig. 3) and also on the scheme of controlled heating. On the end surfaces the insulation boundary conditions have been set
![]() . (7)
. (7)
At the interfaces between metal and cured composite continuity boundary conditions are used
![]() , (8)
, (8)
where lower indices indicate: s – composite spar, m – metallic mould and mandrel, and ![]() is the unit normal vector to the boundary.
is the unit normal vector to the boundary.
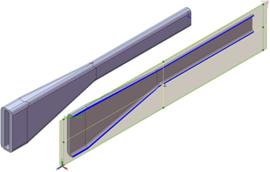
Due to changes of the cured spar cross section (see Fig. 3) the heat is applied to the external surface of a mould by a set of independently controlled electric heaters. Because the cured spar has geometry with symmetry, in the finite element implementation we study only half of the curing system that is heated by two spatially separated heaters that painted by a red color on a Fig. 4. The boundary conditions for the incoming heat flux are
![]() . (9)
. (9)
 (a) (a) |
|
Fig. 3. CAD model of cured spar (a) and finite element (FEM) model of the whole curing system (b)
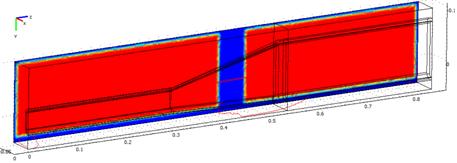
Fig. 4. Spatial distribution of the heated area on the external boundary of the mould
All other external boundaries of the molds irradiate heat according to the Stefan–Boltzmann law
![]() , (10)
, (10)
where ![]() is an ambient temperature,
is an ambient temperature, ![]() is the Stefan–Boltzmann constant, and
is the Stefan–Boltzmann constant, and ![]() is the surface emissivity taken to be 0.5.
is the surface emissivity taken to be 0.5.
Conversion from CAD format of previously developed model (see Fig. 3, a) to the FEM format (see Fig. 3, b) was performed by Comsol Multiphysics built-in converter. FEM model was formulated by coupled Heat Transfer and Partial Differential Equation (PDE) modes where the kinetics equation (1) was presented in the standard PDE form. A ready model can be simulated for performing of static and transient analyses in a real time.
To achieve a good flexibility of control providing the uniform distribution of conversion inside the cured composite piece immediately before applying of compressive pressure as well as at the end of full curing cycle, both electric heaters (see Fig. 4) should be controlled by its own law, i.e. time dependency of performance. These dependencies must be written as a function of time, depending on the parameters, the number of which should provide the necessary flexibility. On the other hand, it is desirable to this number be small as possible to diminish the number of degree of freedom for the optimization problem. Moreover, the objective functions (which to be determined) should be enough sensitive to the variation of these parameters. It has been established that good parameterizations for the one step heating (to the gelation or to full curing states) is the following (see Fig. 5)
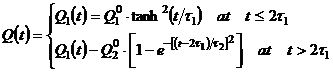 (11)
(11)
where ![]() are the parameters determining the peak and stable values of the generated heat flux, and
are the parameters determining the peak and stable values of the generated heat flux, and ![]() are the time constants. This law provides the gradually increasing heat flux then reaches its maximum value, and afterwards decreases and moves to the stationary value, which depends only on the heat energy which radiates from the mould surfaces (see Fig. 6).
are the time constants. This law provides the gradually increasing heat flux then reaches its maximum value, and afterwards decreases and moves to the stationary value, which depends only on the heat energy which radiates from the mould surfaces (see Fig. 6).
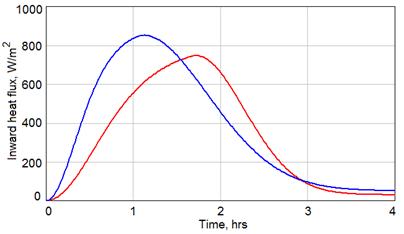
Fig. 5. Two examples of time-dependence for the heaters performance
Optimization Problem Statement
Two different stages of the curing process can be optimized independently - the stage of resin gelation and applying pressure, and further for the stage of fully polymerized solid state starting from the optimal state that has been founded on the previous step. Below we present the developed approach on example of most important first stage of gelation state. For the considered case of two electric heat sources there are 8 parameters ![]() and
and ![]() , which fully determine the control input signals.
, which fully determine the control input signals.
As the curing quality criteria we assume the averaged value of conversion ![]() which should be as close as possible to the desired degree of cure
which should be as close as possible to the desired degree of cure ![]() at the end of monitored curing stage – instant of applying pressure
at the end of monitored curing stage – instant of applying pressure
![]() , (12)
, (12)
and standard deviation of degree of cure
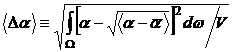 (13)
(13)
that were calculated by integration over the whole cured composite volume ![]() . These integrations have been performed at the end of the simulated real time
. These integrations have been performed at the end of the simulated real time ![]() which could be assigned arbitrarily. Variation of
which could be assigned arbitrarily. Variation of ![]() could slow down or speed up the overall cure time. Such constraint is similar to the same used in [21-23].
could slow down or speed up the overall cure time. Such constraint is similar to the same used in [21-23].
We use here the Pareto approach, supposing assignment a set of choices for all components of objective that are Pareto efficient. By restricting attention to the set of choices that are Pareto-efficient, we can make trade-offs within this set, rather than considering the full range of every parameter. We have a design space with 8 real parameters ![]() ,
, ![]() , and for each design space point there used 2 different quality criteria
, and for each design space point there used 2 different quality criteria ![]() and
and ![]() . The function
. The function ![]() assigns to each design space point
assigns to each design space point ![]() a criteria space point
a criteria space point ![]() . So, let
. So, let ![]() be a set of feasible designs in
be a set of feasible designs in ![]() , then the set which represents the feasible criterion points is
, then the set which represents the feasible criterion points is ![]() , and the image of the set
, and the image of the set ![]() under the action of
under the action of ![]() is
is ![]() . The Pareto set was constructed as a subset of
. The Pareto set was constructed as a subset of ![]() of the feasible criterion points.
of the feasible criterion points.
Due to large dimension of the design space ![]() , the number of simulated designs can be very big, and will require sizable computation time. To reduce it, we simulated only half of the mould geometry and performed calculation consistently narrowing the range of the design variables and approaching the area of acceptable values. The subset
, the number of simulated designs can be very big, and will require sizable computation time. To reduce it, we simulated only half of the mould geometry and performed calculation consistently narrowing the range of the design variables and approaching the area of acceptable values. The subset ![]() of the feasible criterion points was assumed as rectangle
of the feasible criterion points was assumed as rectangle
![]() , (14)
, (14)
where constraint on ![]() corresponds to the maximum dispersion of
corresponds to the maximum dispersion of ![]() equal to 0.005. The maximum performance of both heaters is bounded by its real magnitude.
equal to 0.005. The maximum performance of both heaters is bounded by its real magnitude.
To reproduce topology of the Pareto set, the number numerical experiments at the curing time ![]() =3 hours has been performed. The structure of the feasible criteria subset is presented in Fig. 6.
=3 hours has been performed. The structure of the feasible criteria subset is presented in Fig. 6.
Our numerical experiments have been demonstrated that for the given value ![]() =3 hours the desired value of averaged conversion
=3 hours the desired value of averaged conversion ![]() is reached easily, while providing variation
is reached easily, while providing variation ![]() within a restricted interval encounters difficulties. So, all plots presented below were calculated at the values of
within a restricted interval encounters difficulties. So, all plots presented below were calculated at the values of ![]() , that satisfy constraints (14), i.e. these values belong to the Pareto set or to the Pareto frontier.
, that satisfy constraints (14), i.e. these values belong to the Pareto set or to the Pareto frontier.
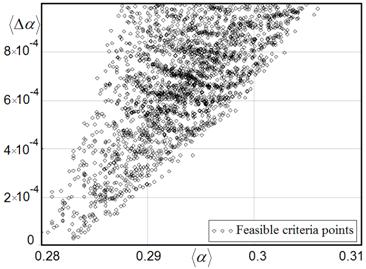
Fig. 6. Scatter plot for points with the feasible criteria
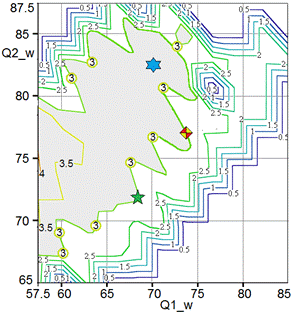
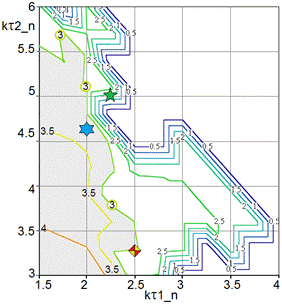
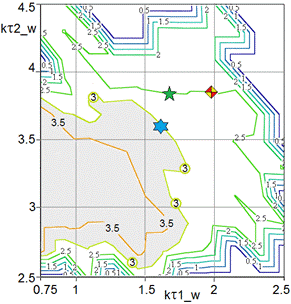
These plots are the reconstructed projections of the criteria points set on the subspaces of design variables. All contour lines on level ‘3’ depict projections of the boundaries of Pareto feasible set on the design subspaces of ![]() , which is projections of Pareto frontier. To improve a visibility of plots all calculated values
, which is projections of Pareto frontier. To improve a visibility of plots all calculated values ![]() have been transformed according to the rule
have been transformed according to the rule
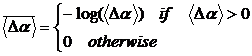 .
.
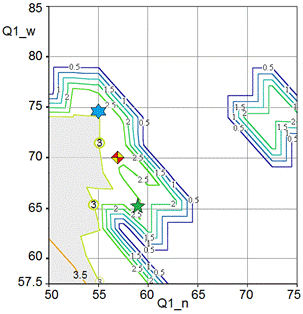
Legends of the coordinate axes in Fig. 7,8 correspond to the parameters in equation (11). The parameters ![]() depicted as Q1_w, Q1_n, Q2_w, and Q2_n, where indices ‘1’ and ‘2’ match to the stages of growing heat flow and reducing heat flow, respectively. Here and after indices ‘w’ relate to the heater installed against thick-walled part of the spar, whereas indices ‘n’ – to the heater that heats the thin-walled part. Time constants
depicted as Q1_w, Q1_n, Q2_w, and Q2_n, where indices ‘1’ and ‘2’ match to the stages of growing heat flow and reducing heat flow, respectively. Here and after indices ‘w’ relate to the heater installed against thick-walled part of the spar, whereas indices ‘n’ – to the heater that heats the thin-walled part. Time constants ![]() were expressed in terms of accepted unit of time equal to
were expressed in terms of accepted unit of time equal to ![]() , and the coefficients
, and the coefficients ![]() , so that, for instance
, so that, for instance ![]() .
.
Results and Discussion
Fig. 7, a, shows that maximum heat flow for thick-walled part should be more intensive at relatively slow rate of heating. To ensure the dwell section on the temperature schedule, the rate of decreasing heat flow for the thin walled section must be reduced. Such choice allows to eliminate an undercooling of thin part. The locations of the level lines corresponding to the best values of the criterion ![]() on two plots for the time constants (see Fig. 8) suggest the feasibility of the slower process may be contrary to the requirements of the fastest technology. It is obvious, for the shorter cycle
on two plots for the time constants (see Fig. 8) suggest the feasibility of the slower process may be contrary to the requirements of the fastest technology. It is obvious, for the shorter cycle ![]() the Pareto set will be less than presented here.
the Pareto set will be less than presented here.
 (a) |
|
|
Fig. 7. Projections of the criterion |
|
|
|
|
|
Fig. 8. Projections of the criterion |
|
To quantitatively estimate the obtained optimization results, our cure system has been simulated at three different schedules with the values of parameters suggested by Pareto analysis and depicted in Figs. 7, 8 by the own markers. These simulation results are presented in Figs. 9 and 10, where dependencies for the first schedule are drawn by solid lines and marked by a diamond, for the second schedule – by the dashed lines with a hexagram marker, and the third schedule- by the dotted lines with a pentagram marker. In Fig. 10 the bold lines relate to the heaters installed against thick walled (root) part of a spar, whereas the fine lines depict the dependencies of an inward heat flow generated by the heaters installed against the thin walled (tip) parts.
 |
|
Fig. 9. Time histories of the process parameters averaged over the cured composite spar: degree of cure (a), its standard deviation (b), temperature (c), and temperature’s standard deviation (d) for three different curing schedules
All three schedules provide a required value of conversion after three hours of curing, but standard deviation of conversion for the third schedule (pentagram marker) exceeds a predetermined value 0.001. The parameters of heating laws (see Eq. 11) for this schedule are outside the Pareto set.
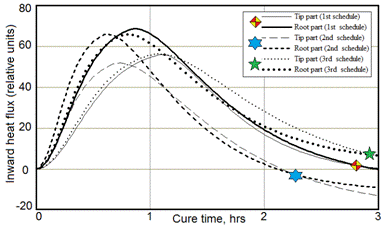
Fig. 10. Time dependencies of the heaters performance for three different curing schedules
The second schedule (marked by a hexagram) provides the best uniformity of a conversion distribution, but this uniformity is achieved by cooling the outer walls of the mould (see Fig. 10). Such a solution encounters the technical difficulties and may not be appropriate due to conditions of manufacturing. However, the required value of ![]() criterion is achieved after 2.1 hours, although the minimum conversion level 0.28 is not reached. This suggests the possibility of modifying the schedule parameters for faster achieve the desired state of the composite.
criterion is achieved after 2.1 hours, although the minimum conversion level 0.28 is not reached. This suggests the possibility of modifying the schedule parameters for faster achieve the desired state of the composite.
The most suitable schedule for the 3 hours process duration is the first, whose parameters are located near Pareto frontier. It is quite obvious that many appropriate schedules constructed in a Pareto set area can be applicable taking into account various kinds of constraints (technological, economical, etc.).
So, Pareto optimization approach has demonstrated a good flexibility satisfying the optimization criteria together with other constraints. Evidently a similar analysis is necessary for a new developed technology with the multi – input multi – output control and at any changes of components and desirable curing schedule.
Conclusions
The model of spatially distributed curing process of epoxy matrix polymeric composite was developed and implemented using FEM. To synthesize the multi-objective optimal control, we perform the transient analysis of the developed model using the projections of Pareto points set on the 8-dimensional space of design variables. Effectiveness and eventual way to use in a practice of the proposed method is illustrated on example of multi – input optimal control synthesis for the closed mould curing of composite spar.
Acknowledgments
The authors wish to acknowledge the financial support from the Russian Foundation for Basic Research (Grants 10-08-13300-РТ_оми, 13-08-9091213) that are fulfilled at the Russian – Taiwanese cooperation.
References:
- Akovali, G. Handbook of composite fabrication // RAPRA Techn. LTD., Shawbury, UK, 2002, 205 pp..
- Concise Encyclopedia of Composite Materials // Ed. A. Mortensen, 2nd ed., Elsevier, Oxford, UK, 2007, 989 pp.
- Heinrich C. et al. Generation of heat and stress during the cure of polymers used in fiber composites // International Journal of Engineering Science, Vol. 53, 2012, pp. 85-111.
- Babu, B.J.C., Prabhakaran, R.T. D., and Agrawal, V.P. Quality Evaluation of Resin Transfer Molded Products // Journal of Reinforced Plastics and Composites, Vol. 27, 2008, pp.559-581.
- Chang, C.-Y., Huang, L.-W., and Chou, T.-Y. Effect of Process Variables on the Quality of Compression Resin Transfer Molding // Journal of Reinforced Plastics and Composites, Vol. 25, 2006, pp.1027-1037.
- Johnson, M.S., Rudd, C.D., and Hill, D.J. Cycle Time Reductions in Resin Transfer Moulding Using Microwave Preheating // Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, Vol. 209, 1995, pp.443-453.
- Garschke, C., Weimer, C., Parlevliet, P.P., and Fox, B.L. Out-of-Autoclave Cure Cycle Study of a Resin Film Infusion Process Using In Situ Process Monitoring // Composites: Part A, Vol.43, 2013, pp. 935–944.
- Hardis R. et al., Cure Kinetics Characterization and Monitoring of an Epoxy Resin Using DSC, Raman Spectroscopy, and DEA // Composites: Part A, Vol.49, 2013, pp. 100–108.
- Hof, P.M.J., Scherer, C., and Heuberger, P.S.C. Model-Based Control: Bridging Rigorous Theory and Advanced Technology, Springer, Berlin / Heidelberg, 2009, 245 pp.
- Franke, R. and Doppelhamer, J. Integration of Advanced Model Based Control with Industrial IT // in: Lecture Notes in Control and Information Sciences, Vol.358, Springer, Berlin / Heidelberg, 2007, pp. 399-406.
- Липа, В.Б. Алгоритм и программная реализация адаптивного метода обучения искусственных нейронных сетей [Электронный ресурс] // «Инженерный вестник Дона», 2012, №1. – Режим доступа: http://ivdon.ru/uploads/article/doc/articles.626.big_image.doc (доступ свободный) – Яз. рус.
- Kamal, M.R. and Sourour, S. Kinetics and Thermal Characterization of Thermoset Cure // Polymer Engineering and Science, Vol.13, 1973, pp. 59-64.
- Aboulach, R., Boujena, S., and Pousin, J. A Numerical Analysis of Resin Transfer Molding // Journal of Condensed Matter, Vol. 5, No.1, 2004, pp 4-9.
- Garschke, C., Parlevliet, P.P., Weimer, C., and Fox, B.L. Cure Kinetics and Viscosity Modelling of a High-Performance Epoxy Resin Film // Polymer Testing, Vol. 32, 2013, pp.150-157.
- Um, M.-K., Daniel, I.M., and Hwang, B.-S. A Study of Cure Kinetics by the Use of Dynamic Scanning Calorimetry // Composites Science and Technology, Vol. 62, 2002, pp. 29-40.
- Zhang, J., et al. Investigation of Curing Kinetics of Sodium Carboxymethyl Cellulose/Epoxy Resin System by Differential Scanning Calorimetry // Thermochimica Acta, Vol. 549, 2012, pp. 63– 68.
- Van Assche, G., Swier, S., Van Mele, B. Modeling and Experimental Verification of the Kinetics of Reacting Polymer Systems // Thermochimica Acta, Vol. 388, 2002, pp. 327-341.
- Shevtsov, S. et al. Optimization of the Composite Cure Process Based on Thermo-Kinetics Model // Advanced Materials Research, Vol. 569, 2012, pp 185-192.
- Calabrese, L. et al. Thermal and Rheological Characterization of a Thermoset Matrix for Filament Winding Modelling // Advanced Composite Letters, Vol.13, Issue 1, 2004, p.34-37.
- Harsch, M., Karger-Kocsis, J., and Holst, M.Influence of Fillers and Additives on the Cure Kinetics of an Epoxy/Anhydride Resin // European Polymer Journal, Vol. 43, 2007, pp. 1168-1178.
- Pandiyan, K.R.R., Kundu, G., Neogi, S., and Patel, J. Development of Manufacturing Technology for Cab Front Using Resin Transfer Molding Process // Journal of Composite Materials, Vol. 44, 2010, pp.2217-2233.
- Saad, A. et al. Optimization of the Cycle Time in Resin Transfer Molding Process by Numerical Simulation // Journal of Reinforced Plastics and Composites, Vol.31, 2012, pp.1388 – 1399.
- Sorrentino, L. et al. Cure Process Design to Manufacture Composite Components with Variable Thickness by a Closed Die Technology // Proceedings of the International Conference on Composite Materials ICCM17, Edinburgh, Scotland, 2009, 11 p.
 (b)
(b)