Об исследовании бортовой интегрированной системы управления движением летательного аппарата с коррекцией координат
Аннотация
Дата поступления статьи: 18.11.2013Работа посвящена вопросам исследования алгоритмов функционирования подсистемы управления, входящей в состав бортовой интегрированной системы управления летательным аппаратом и используемой на заключительном участке траектории движения. Алгоритмы функционирования подсистемы управления синтезированы на основе теории оптимизированных дельта-преобразований второго порядка с использованием принципа управления перевернутым маятником на тележке. В ходе исследований, проводимых на основе имитационного моделирования с использованием разработанной программной модели, оценивается как итоговая ошибка рассеивания, так и вклад в нее различных подсистем.
Ключевые слова: управление движением на конечном участке, летательный аппарат, бортовая интегрированная система управления, оптимизированные дельта-преобразования второго порядка, автономная система ближней радионавигации, имитационное моделирование, программная модель
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Введение
При модернизации существующих и разработке новых перспективных беспилотных летательных аппаратов (ЛА) одной из актуальных задач является создание системы управления, обеспечивающей решение задач предельно быстрой отработки отклонения от заданной траектории (по результатам коррекции) и вывода ЛА в точку приземления с необходимой точностью. В настоящее время наибольший интерес представляет создание высокоточных и прецизионных систем управления.
Для минимизации ошибки рассеивания используются интегрированные системы управления, комплексирующие получаемые по нескольким независимым навигационным полям данные о параметрах движения объекта [1, 2].
Рассматриваемая в работе бортовая интегрированная система управления (БИСУ) представляет собой сложную техническую систему, имеющую в своем составе в качестве подсистем систему управления, инерциальную навигационную систему (ИНС) и бортовой модуль автономной системы ближней радионавигации (АСБРН). Движение ЛА под управлением БИСУ осуществляется на заключительном участке траектории.
Подсистема управления, входящая в состав БИСУ, построена на основе теории и алгоритмов оптимизированных дельта-преобразований второго порядка с использованием принципов управления тележкой с перевернутым маятником. Особенностями использования методологии дельта-преобразований второго порядка является возможность синтеза алгоритмов цифрового управления для механических объектов со сложным нелинейным описанием, обеспечение оптимизированных по быстродействию и точности процессов [3, 4].
Летательный аппарат представляет собой объект, в котором центр масс и точка приложения силы не совпадают. В данном случае для решения проблемных вопросов управления представляет интерес использование принципов управления тележкой с перевернутым маятником [5-7]. Методологические особенности и математический аппарат синтеза алгоритмов управления на основе дельта-преобразований с использованием принципа перевернутого маятника впервые подробно освещены в работах [3, 8]. В настоящее время ведутся исследования по оценке применимости разработанных алгоритмов для управления высокоскоростными беспилотными летательными аппаратами с учетом необходимости взаимодействия с навигационными подсистемами, входящими в состав БИСУ ЛА.
Инерциальные навигационные системы удовлетворяют требованиям универсальности, автономности, помехозащищенности и помехоустойчивости, а также скрытности работы, однако точность выходной информации в ИНС зависит от точности чувствительных элементов, а ошибка в определении навигационных параметров накапливается с течением времени. Для повышения точности, особенно в случае бесплатформенных ИНС, необходимо периодически корректировать данные инерциальной навигационной системы по показаниям внешних приборов [9].
Наиболее распространен подход к комплексированию ИНС со спутниковой навигационной системой (СНС) GPS, ГЛОНАСС и т.д. В то же время использование для формирования корректирующих навигационных определений СНС в некоторых условиях может быть затруднено или даже невозможно [10, 11].
В данной работе в качестве корректирующей внешней навигационной системы рассматривается автономная система ближней радионавигации, а также информационно-алгоритмическое обеспечение наземного и бортового сегментов АСБРН [12, 13].
Для анализа показателей эффективности разработанных алгоритмов управления в целом используется метод компьютерного моделирования процесса функционирования БИСУ. Данный подход является инструментом анализа технических систем высокой сложности и позволяет выполнить моделирование входных и внешних воздействий, воспроизвести работу моделируемой системы (моделирующий алгоритм), провести интерпретацию и обработку результатов моделирования [14].
Для получения достоверных оценок характеристик исследуемой системы реализуется многократное моделирование процесса ее функционирования, варьирование исходных данных. В качестве входных данных для имитационной модели выступают параметры законов распределения случайных величин, соответствующих измерениям ИНС и АСБРН.
В работе рассматриваются особенности взаимодействия подсистемы управления с навигационными подсистемами в составе БИСУ, даются краткие сведения о математических и процедурных основах обработки данных в подсистемах БИСУ, приводится архитектура программной модели, раскрывается схема проведения эксперимента. В завершении работы приведены обобщенные данные о результатах модельных исследований интегрированной системы управления, позволяющие сделать вывод об адекватности разработанной модели и качественных характеристиках синтезированных алгоритмов управления.
Взаимодействие подсистемы управления с навигационными подсистемами в составе БИСУ
Рассматривается вариант построения и функционирования БИСУ, временной интервал работы которого (реализованный в программной модели), ограничен движением летательного аппарата на заключительном участке траектории. Организация взаимодействия по данным между подсистемами, входящими в состав БИСУ, показана на рис. 1.
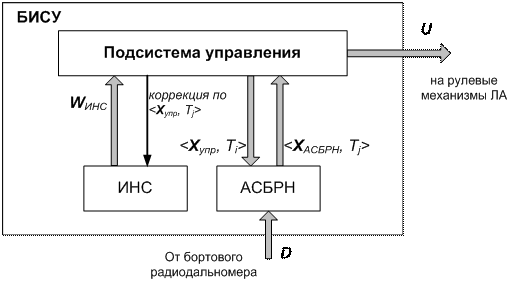
Рис. 1 – Схема обмена данными между подсистемами БИСУ
Подсистема управления взаимодействует с инерциальной навигационной системой (ИНС) и бортовым модулем автономной системы ближней радионавигации (АСБРН).
Автономная ИНС формирует и передает в подсистему управления с некоторым постоянным темпом (порядка сотен герц) вектор WИНС с параметрами ориентации и положения летательного аппарата.
Бортовой модуль АСБРН выполняет обработку вектора мгновенных дальномерных измерений D, поступающего от радиодальномера (с темпом обновления порядка 50..100 Гц) и по результатам обработки формирует вектор XАСБРН, характеризующий пространственное положение ЛА в системе координат, связанной с искусственным навигационным полем. Временной интервал между моментами формирования вектора XАСБРН (вектор передается в подсистему управления в паре с параметром Tj, соответствующим моменту времени измерения дальностей бортовым радиодальномером) может варьироваться вследствие кратковременных "пропаданий" радиосигналов, нарушения целостности навигационного поля, особенностей процедур обработки данных в информационно-алгоритмическом обеспечении АСБРН.
Обратная связь от подсистемы управления к бортовому модулю АСБРН используется для передачи информации о текущих пространственных координатах ЛА Xупр (для момента времени Ti). В бортовом модуле АСБРН эти данные могут использоваться в качестве внешней вспомогательной информации, например, на этапе вычисления координат объекта по совокупности дальномерных измерений (при ограниченном количестве видимых радиомаяков), или на этапе реализации алгоритма автономного контроля целостности искусственного навигационного поля АСБРН.
Комплексирование показаний ИНС и бортового модуля АСБРН выполняется с помощью подсистемы управления, что, фактически, соответствует разомкнутой схеме комплексирования. Обе навигационные системы работают независимо друг от друга, но периодически выполняется коррекция ИНС по данным бортового модуля АСБРН. Процедурно коррекция ИНС заключается в перезапуске алгоритма ИНС с новыми начальными условиями по координатам, данные о которых поступают от АСБРН.
Такая архитектура обеспечивает независимость систем (исключая моменты перезапуска или коррекции) и информационную избыточность общей структуры, необходимую для обнаружения и изоляции отказов при низкой надежности навигационных устройств [15, 16].
Выбор разомкнутой схемы комплексирования позволяет:
- использовать в составе БИСУ готовый модуль ИНС;
- добиваться повышения точности определения координат ЛА при сохранении возможности получения позиционной, скоростной и угловой информации, необходимой для целей управления с высокой частотой, свойственной ИНС.
По результатам обработки полученных навигационных измерений подсистема управления на основе синтезированного алгоритма управления формирует вектор управляющих воздействий U, который с заданным темпом выдается на органы управления ЛА.
Этапы обработки данных в подсистеме управления
Синтез алгоритмов цифрового управления ориентирован для высокоскоростного ЛА баллистического типа [17]. Модельное описание базируется на системе уравнений Эйлера, включающей три уравнения для сил и три уравнения для моментов в проекциях на оси связанной системы координат (СК) [18]. Уравнения аэродинамических сил, описывающие движение центра масс ЛА:
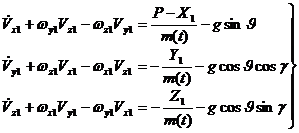 .
.
Уравнения моментов, описывающие вращение вокруг центра масс (учитывая, что ![]() ,
, ![]() ):
):
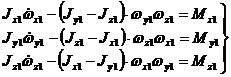 ,
,
где m(t) – масса ЛА, ![]() ; g – ускорение свободного падения; ϑ - угол тангажа, γ- угол рыскания; ϖx1, ϖy1, ϖz1 – угловые скорости вращения осей связанной СК (OX1, OY1, OZ1); X1, Y1, Z1 – проекции внешних сил на оси OX1, OY1, OZ1 связанной СК; Mx1, My1, Mz1 – проекции аэродинамического момента на оси связанной СК:Mx1, – момент крена (вокруг оси OX1),My1 – момент рыскания (вокруг оси OY1),Mz1 – момент тангажа (вокруг оси OZ1); Jx1, Jy1, Jz1 – моменты инерции ЛА относительно главных осей инерции; Vx1, Vy1, Vz1 – проекции скорости V на оси связанной СК.
; g – ускорение свободного падения; ϑ - угол тангажа, γ- угол рыскания; ϖx1, ϖy1, ϖz1 – угловые скорости вращения осей связанной СК (OX1, OY1, OZ1); X1, Y1, Z1 – проекции внешних сил на оси OX1, OY1, OZ1 связанной СК; Mx1, My1, Mz1 – проекции аэродинамического момента на оси связанной СК:Mx1, – момент крена (вокруг оси OX1),My1 – момент рыскания (вокруг оси OY1),Mz1 – момент тангажа (вокруг оси OZ1); Jx1, Jy1, Jz1 – моменты инерции ЛА относительно главных осей инерции; Vx1, Vy1, Vz1 – проекции скорости V на оси связанной СК.
Синтез алгоритмов управления по каналам тангажа и рыскания осуществляется на основе методологии управления положением перевернутого маятника на тележке и положением тележки [3, 8]. Физическая сущность процессов управления маятником и тележкой состоит в следующем. С помощью одного управляющего воздействия устанавливаются небольшие по углу отклонения перевернутого маятника от вертикали. Знак угла отклонения задается исходя из обеспечения необходимого направления движения тележки по заданной траектории с обеспечением минимизации ошибки положения тележки.
На основе синтезированных алгоритмов цифрового управления ЛА с использованием дельта-преобразований второго порядка и принципов управления маятником на тележке реализуются следующие процессы. На каждом дискретном шаге на вход алгоритмов управления поступают измеренные ошибка отклонения от заданной траектории и производная этой ошибки. По каналу тангажа (рыскания) формируется одно управляющее воздействие. С помощью этого воздействия устанавливается определенный по значению модуля угол атаки (рыскания). Знак данного угла определяется на основе анализа изменения ошибки расположения центра тяжести ЛА относительно заданной траектории с обеспечением минимизации этой ошибки. Синтез алгоритмов управления по каналу крена реализуется на основе "немаятниковой" методологии, освещенной в [3].
Предполагается, что измеряемыми или вычисляемыми в процессе реального движения являются величины:
- углы ориентации ЛА γ, ϑ, Ψ;
- углы направления осей ЛА относительно вектора скорости Α, β;
- пространственные координаты ЛА в земной СК yg, zg, xg;
- скорости ЛА в связанной СК Vx1, Vy1,Vz1;
- проекции внешних сил на оси связанной СК X1, Y1, Z1 ;
- проекции аэродинамического момента на оси связанной СКMx1,My1,Mz1.
Разработанные алгоритмы цифрового управления нацелены на обеспечение оптимизации по быстродействию и точности, что представляет особый интерес для конечного участка траектории ЛА. Низкая вычислительная трудоемкость этих алгоритмов позволяет реализовывать управление на базе современных образцов вычислительной техники в реальном масштабе времени.
Особенности моделирования алгоритмов функционирования навигационных подсистем в рамках имитационной модели
Автономная система ближней радионавигации. АСБРН предоставляет возможность определения местоположения летательного аппарата (ЛА) по совокупности мгновенных дальномерных измерений от ЛА до наземных радиомаяков, образующих искусственное навигационное поле (ИНП) с известной геометрической конфигурацией. Навигационные измерения совместно с предварительно введенными в бортовой вычислитель АСБРН данными об ИНП позволяют получить вектор пространственного положения ЛА XАСБРН путем решения стандартной для дальномерных навигационных систем системы уравнений [2, 19]:
![]() ,
,
где x, y, z – координаты ЛА; xi, yi, zi – координаты i-го радиомаяка в выбранной локальной системе координат (ЛСК) с центром в заданной точке приземления ЛА; Di – измеренная бортовым радиодальномером АСБРН дальность до i-го радиомаяка.
В рамках АСБРН поддерживается банк алгоритмов решения системы уравнений, основанных на итерационных и конечных математических методах. Принятие решения о выборе конкретного алгоритма и используемой подгруппы радиомаяков осуществляется в бортовом модуле АСБРН на основе загруженного в вычислитель в виде специальной структуры данных "дерева отказов", обеспечивающего поиск оптимальной пары <алгоритм решения, подгруппа РМ> в данной области траектории. Информация о работоспособных маяках формируется в модуле автономного контроля целостности навигационного поля.
С учетом результатов анализа разработанных алгоритмов функционирования АСБРН выполненного, в частности, в работах [13, 20], выявлены следующие факторы, которые оказывают наиболее существенное влияние на точность, надежность и быстродействие расчета и выдачи вектора координат потребителя XАСБРН:
- конфигурация ИНП, количество и геометрическое расположение радиомаяков в котором оказывает существенное влияние на точность расчета координат объекта (Dilution of Precision, DOP);
- "полная" ошибка оценки измеренной дальности до каждого радиомаяка бортовым радиодальномером АСБРН. Под "полной" ошибкой понимается суммарная ошибка измерения параметров радиосигнала, и приведенной к эквивалентной ошибке дальности погрешность позиционирования радиомаяка;
- вероятность отказа каждого радиомаяка. Вектор вероятностей отказа используется для однократного формирования подмножества радиомаяков, доступных для расчета вектора XАСБРН в очередном опыте. Выход из строя маяков (обнаруженный и изолированный отказ) эквивалентен изменению конфигурации ИНП;
- интервал времени расчета вектора XАСБРН в бортовом модуле АСБРН, зависящий как от степени избыточности навигационного поля, так и от производительности бортового вычислителя АСБРН.
Инерциальная навигационная система. Поскольку для определения параметров ориентации и положения объекта планируется использовать готовый модуль ИНС, то представляет интерес выбор ИНС такого класса точности, который может быть определен на основе результатов экспериментальных исследований БИСУ [21, 22].
На данном этапе в качестве фактора, оказывающего наиболее существенное влияние на точность расчета вектора WИНС с параметрами ориентации и положения, выбрана скорость накопления погрешности определения координат (измеряемая в м/сек) по каждой из осей связанной системы координат ЛА.
Влияние рассмотренных в данном разделе факторов на конечное рассеивание БИСУ оценивается при проведении экспериментов с использованием метода статистического моделирования.
Архитектура программной модели бортовой интегрированной системы управления ЛА
Для проведения экспериментальных исследований и проведения оценки точностных характеристик разработанных алгоритмов и методов была разработана специализированная программная модель, учитывающая основные аспекты функционирования БИСУ ЛА. Программную модель системы можно разделить на несколько обособленных функциональных блоков, реализующих определенную часть функциональности (см. рис. 2).
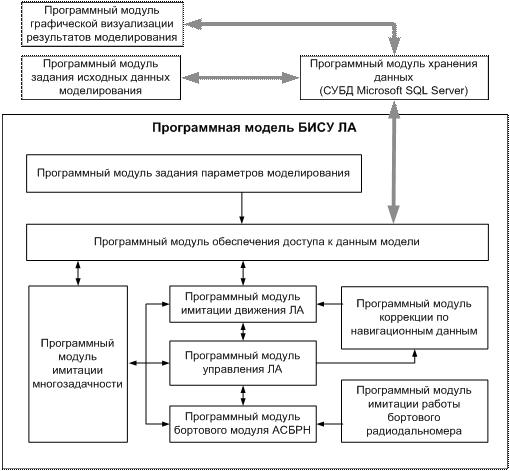
Рис. 2 – Архитектура программной модели БИСУ ЛА
На рис. 2 в виде прямоугольных блоков изображаются отдельные функциональные составляющие программной модели, а в виде стрелок – потоки данных между этими блоками. Таким образом, функциональные компоненты взаимодействуют только с теми блоками, данные от которых им необходимы в процессе работы программы и не связаны другими блоками. Это является дополнительной гарантией корректности проводимых вычислений, так как ограничивает функциональный блок только теми данными, которые ему действительно необходимы и запрещает доступ к тем данным, доступ к которым блок получить не может.
Следует особо отметить блоки, находящиеся в верхней части схемы приведенной на рис. 2. Поскольку функциональность данных блоков сильно обособленна от остальной части системы, они реализованы в виде отдельных программ-проектов (в рамках единого решения).
Программа написана на языке C# и реализована в интегрированной среде Microsoft Visual Studio 2008.
Экспериментальные исследования
Основными задачами обработки экспериментальных данных и проведения моделирования являются:
- исследование характеристик алгоритмов цифрового управления БИСУ ЛА на основе алгоритмов оптимизированных дельта-преобразований второго порядка в различных режимах функционирования на завершающем участке траектории;
- формирование статистических оценок ошибки рассеивания в точке приземления ЛА, интегрирующей в себе накопленную ошибку ИНС к моменту начала управления, ошибку интегрирования координат ЛА (с накоплением), ошибку определения местоположения ЛА с помощью АСБРН, динамическую ошибку управления, а также ошибку, которая вызвана временными задержками расчетов.
Проведены две серии экспериментов.
Первая серия экспериментов предназначена для исследования возможностей синтезированных алгоритмов цифрового управления на завершающем участке траектории. Моделирование работы АСБРН и коррекция координат имитируются путем однократной выставки отклонения пространственных координат ЛА и углов ориентации ЛА в пространстве в момент начала управления на конечном участке траектории. Результатами расчета являются оценки ошибки касания ЛА с землей (относительно заданной точки касания), предельные значения углов атаки и скольжения, предельные перегрузки.
По результатам первой серии экспериментов, в которой не учитывается влияние погрешностей навигационных подсистем, получены ошибки рассеивания на уровне единиц метров, обеспечиваемые подсистемой управления ЛА при компенсации начальных отклонений от заданной траектории движения на уровне 3s = 500 м за 4..4,5 сек. Следует отметить, что применение дополнительных методик адаптации позволило до одного метра снизить ошибку рассеивания подсистемы управления ЛА.
Вторая серия включает в себя эксперименты, позволяющие получить комплексную оценку точностных характеристик разработанной системы управления ЛА с коррекцией координат по информации от АСБРН. Величина ошибки касания ЛА с землей является результатом комплексного воздействия всех моделируемых факторов, рассмотренных в предыдущих разделах данной работы. Полученные в ходе проведения второй серии статистических экспериментов результаты свидетельствуют о возможности получения (для рассматриваемых навигационных подсистем в составе БИСУ) итоговой ошибки рассеивания на уровне 3s = (20..25) м при однократной коррекции от АСБРН (см. иллюстрацию на рис. 4), и на уровне до 3s = (5..7) м при множественной коррекции.
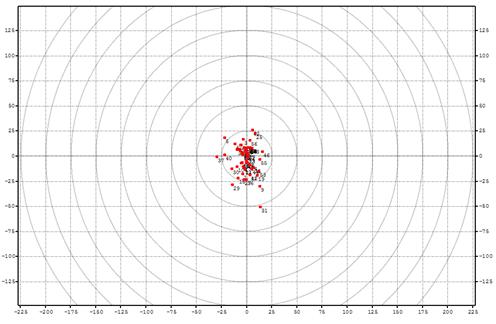
Рис. 4 – Ошибка рассеивания в точке приземления ЛА по результатам статистического имитационного моделирования в режиме однократной коррекции
Заключение
Качественные характеристики синтезированного алгоритма управления ЛА на основе оптимизированных дельта-преобразований второго порядка с использованием принципа перевернутого маятника соответствует уровню высокоточных и прецизионных систем управления.
Существующие навигационные подсистемы БИСУ (характеристики которых были использованы при проведении имитационного моделирования) оказывают больший вклад в итоговую погрешность рассеивания по сравнению с динамической ошибкой разработанной подсистемы управления.
По результатам проведенных исследований сделан вывод о целесообразности совершенствования навигационных подсистем БИСУ ЛА с целью обеспечения более высоких показателей точности рассеивания, потенциально обеспечиваемых разработанными алгоритмами цифрового управления на основе оптимизированных дельта-преобразований второго порядка с использованием принципа перевернутого маятника.
Литература:
1. ГЛОНАСС. Принципы построения и функционирования /Под ред. А.И. Перова, В.Н. Харисова. Изд. 4-е, перераб. и доп. – М.: Радиотехника, 2010. – 800с.
2. Сетевые спутниковые радионавигационные системы /В.С. Шебшаевич, П.П. Дмитриев, Н.В. Иванцевич и др.: Под ред. В.С. Шебшаевича. – 2-е изд., перераб. и до. – М.: Радио и связь, 1993. – 408 с.
3. Кравченко П.П. Оптимизированные дельта-преобразования второго порядка. Теория и применение. – М.: Радиотехника, 2010. – 288 с.
4. Кравченко П.П.Синтез алгоритмов цифрового управления на основе оптимизированных дельта-преобразований второго порядка при неполной информированности о системе //Труды Международной конференции "Идентификация систем и задачи управления". М.: ИПУ РАН, 2000. – 34 с.
5. Franklin, G.F., Powell, J.D., Emami-Naeini, A. Feedback Control of Dynamic Systems (6th Edition). – Prentice Hall, 2009. – P. 840.
6. Verma, M.K., Jha, S.K., Gaur, P., Mittal, A.P Artificial intelligence based control of 3D inverted pendulum // 2012 IEEE Fifth India International Conference on Power Electronics (IICPE), 6-8 Dec. 2012. – pp. 1-5.
7. Нефедов Н.Ю., Решетников А.Г., Ульянов С.В. Интеллектуальное управление физическим динамически неустойчивым объектом "карета-перевернутый маятник". Ч. 1: технология мягких вычислений [Электронный ресурс] // "Системный анализ в науке и образовании", 2012, № 3. – Режим доступа: http://www.sanse.ru/download/132 (доступ свободный) – Загл. с экрана. – Яз. рус.
8. Кравченко, П.П. Синтез алгоритмов цифрового управления перевернутым маятником на тележке с использованием аппарата дельта-преобразований второго порядка. [Текст]: // "Мехатроника, автоматизация, управление", 2012, № 5 – М.: Новые технологии. – 72 с.
9. Пешехонов В.Г. Ключевые особенности современной автономной навигации //Гироскопия и навигация. – 1996. - № 1 (12). С. 48-55
10. Основы теории систем управления высокоточных ракетных комплексов Сухопутных войск /Б.Г. Гурский, М.А. Лющанов, Э.П. Спирин,; Под ред. В.Л. Солунина. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. – 328с.
11. Lin C.-F. Modern Navigation, Guidance, and Control Processing. –Prentice-Hall: New Jersey, 1991. – 696 pp.
12. Хусаинов Н.Ш. Принципы построения информационно-алгоритмического обеспечения перспективных систем определения местоположения ЛА по информации от автономной системы ближней радионавигации //Известия ЮФУ. Технические науки. Тематический выпуск "Интеллектуальные САПР". - Таганрог: Изд-во ТТИ ЮФУ, 2007, № 2 (77). С. 130-135.
13. Хусаинов Н.Ш., Кравченко П.П., Щербинин В.В., Шаповалов В.А. Анализ составляющих ошибки навигации и наведения летательного аппарата, использующего для коррекции движения автономную систему ближней радионавигации //Известия ЮФУ. Технические науки. Тематический выпуск "Перспективные системы и задачи управления". - Таганрог: Изд-во ТТИ ЮФУ, 2010. № 3 (104). С.55-59.
14. Афанасьева О.В., Голик Е.С., Первухин Д.А. Теория и практика моделирования сложных систем: Учеб. пособие. – СПб.: СЗТУ, 2005. – 131 с.
15. Poreba M. Use of Integrated GPS and INS Systems in Aerial Photogrammetry //Geomatics and Environmental Engineering. – 2011. – Vol. 5, N.3. – P. 79-87.
16. Щербань И.В., Толмачев С.А., Конев Д.С. Слабосвязанный алгоритм интегрированной инерциально-спутниковой навигационной системы транспортного средства [Электронный ресурс] // "Инженерный вестник Дона", 2013, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2013/1821 (доступ свободный) – Загл. с экрана. – Яз. рус.
17. Кравченко П.П., Хусаинов Н.Ш. Применение методологии синтеза алгоритмов цифрового управления перевернутым маятником на тележке с использованием аппарата оптимизированных дельта-преобразований второго порядка для управления беспилотным летательным аппаратом на конечном участке траектории //Системы управления беспилотными космическими и атмосферными летательными аппаратами: Тезисы докладов II Всероссийской научно-технической конференции. - М.: МОКБ "Марс", 2012. – С.70-71.
18. Аэродинамика ракет: в 2-х кн. Кн. 1. Пер. с англ. /Под ред. М. Хемша, Дж. Нилсена. – М.: Мир, 1989. – 426с.
19. Барабанов О.О., Барабанова Л.П. Математические задачи дальномерной навигации. – М.: ФИЗМАТЛИТ, 2007. – 272с.
20. Хусаинов Н.Ш. Программные средства моделирования решения задачи определения местоположения ЛА с использованием АСБРН //Вопросы оборонной техники. Сер. 9. Специальные системы управления, следящие приводы и их элементы. - М.: ФГУП "НТЦ "Информтехника". - 2007. - Вып. 1(230) - 2(231). С.15-17
21. Хацько Н.Е. О возможности использования инерциальных датчиков низкого и среднего класса точности в системах автоматического управления полетом летательного аппарата [Электронный ресурс] // "Инженерный вестник Дона", 2013, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2013/1756 (доступ свободный) – Загл. с экрана. – Яз. рус.
22. Управление и наведение беспилотных маневренных летательных аппаратов на основе современных информационных технологий / Под ред. М.Н. Красильщикова и Г.Г. Себрякова. – М.: ФИЗМАТЛИТ, 2003. – 280с.