Достаточное условие квазикорректности смешанного краевого условия для поверхностей второго порядка

Аннотация

Н.Н. Солохин

Дата поступления статьи: 30.10.2013

В работе изучаются бесконечно малые изгибания поверхностей положительной кривизны с краем, подчинённых на краю внешней связи смешанного типа. Устанавливается квазикорректность такой внешней связи при условии, что векторное поле принадлежит поверхности

Ключевые слова: поверхность положительной кривизны, бесконечно малые изгибания, поле смещений, поле вращений, собственное векторное поле, модельная задача

05.13.18 - Математическое моделирование, численные методы и комплексы программ

В работах [1] и [2] впервые был изучен вопрос о квазикорректности внешней связи вида
      (1),                                                
где  - однородный аддитивный оператор,  - векторное поле смещения при бесконечно малом изгибании поверхности,  - известная функция.
В работе [3] наряду с общими результатами была рассмотрена реализация такой внешней связи для поверхностей второго порядка.
Следующим этапом явилось изучение квазикорректности внешней связи (краевого условия) смешанного типа:  
    (2),                                           
где  и  – векторные поля смещения и вращения бесконечно малого изгибания поверхности,  и  – векторные поля, заданные вдоль края поверхности,  – некоторые функции, заданные вдоль границы поверхности.
В этом направлении было получено ряд теорем, представляющих немаловажный интерес в теории бесконечно малых изгибаний поверхностей. Рассмотрение реализаций этих общих теорем для поверхностей второго порядка дало более широкую и глубокую картину распределения собственных векторных полей краевого условия смешанного типа. В частности были рассмотрены сферические сегменты и сечения параболоида вращения и дана картина распределения собственных векторных полей в таких сечениях.
Краевое условие (2) назовём квазикорректным с р степенями свободы, если однородное условие () совместимо с р линейно независимыми бесконечно малыми изгибаниями поверхности S, а неоднородное условие совместимо с бесконечно малыми изгибаниями для любой функции . Векторные поля  и  назовём собственными, если условие (2) не является квазикорректным [1, c.152].
Пусть ,  – односвязная поверхность второго порядка положительной кривизны  с краем , .  Пусть далее на границе  поверхности  заданы вещественные функции а, b и с и векторное поле  класса ,  . Считаем, что векторное поле  не принадлежит поверхности. В настоящей работе рассматривается случай, когда , где  – единичный вектор нормали к поверхности.
Рассмотрим внешнюю связь
   (3)                                             
Пусть  – единичный касательный к краю  вектор;  – единичный вектор нормали поверхности ,  – тангенциальная нормаль.
Таким образом, вдоль края  поверхности мы имеем подвижный репер  и некоторое поле  класса , . Пусть  – проекция  на касательную к  плоскость. Считаем также, что векторное поле  не касательно к границе поверхности в каждой точке края. Обозначим  – угол между  и , где отсчет производится в положительном направлении, если смотреть со стороны вектора . Обозначим угол между  и  через , считая, что отсчёт производим от  до  против хода часовой стрелки, если смотреть из конца вектора . В та­ких обозначениях векторное поле  однозначно определяется заданием углов  и  как функций длины дуги контура.
Теорема. Пусть вдоль края   задано семейство векторных полей , определяемых углами  и , где  – фиксированная функция из интервал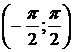а , а  произвольная функция. Пусть, кроме того,  и . Тогда существует константа , зависящая от поверхности , края  и векторного поля , такая, что при 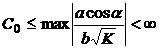 поверхность второго порядка с внешней связью (3) является квазикорректной с 3 степенями свободы.
Доказательство: Краевое условие  (3) приводится к виду
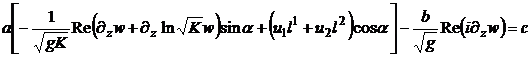    (4)
где  - комплексная функция изгибания [6, с. 403],  - координаты вектора  в базисе , .
Как известно из [6] для поверхностей второго порядка уравнение бесконечно малых изгибаний можно записать в виде:
.
Обозначим ,  и выполним замену искомой функции . Тогда краевое условие (4) при  перепишем в виде
      (5).
Будем считать, что некоторая внутренняя точка поверхности второго порядка закреплена вместе с касательной плоскостью в ней. Не нарушая общности, можно взять в качестве этой точки точку  и поэтому искомая функция  должна в точке  иметь нуль второго порядка, т.е. , где  – голоморфная в области  функция.
Сделаем замену функции , где  – аналитическая функция, непрерывная в , обращаясь в нуль в начале координат, не равная нулю на границе и удовлетворяющая там краевому условию  .
Решение  имеет вид , где  – искомая функция, не обращающаяся в нуль ни в одной точке области и на её границе.
Введём обозначения: , ,  , , , , , , где  – гармонические функции, тогда имеем ,  при .
При этих обозначениях краевое условие (5) приводится к виду:

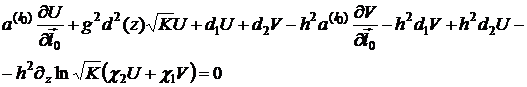
Полученная краевая задача
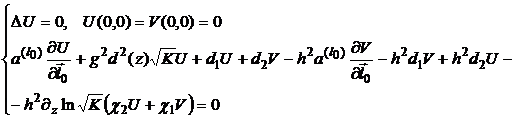     (6)
имеет только нулевое решение. Тогда с помощью преобразования  имеем  в . Значит, задача

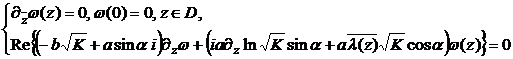
имеет только нулевое решение.
Таким образом, можно утверждать, что существует константа , зависящая от поверхности , края  и векторного поля , такая, что при  поверхность второго порядка с условием (4) является жёсткой.

Литература:

1. В.Т.Фоменко. О квазикорректности внешних связей в теории бесконечно малых изгибаний. СМЖ. 1974. Т.15. №1. С.152-161.
2. В.Т.Фоменко. О квазикорректности внешних связей в теории бесконечно малых изгибаний поверхностей. ДАН. 1973. Т.212. №6. С.1305-1308.
3. Казак В.В. Исследование условия обобщённого скольжения в теории бесконечно малых изгибаний: дисс. канд. физ. – мат. наук. Ростов – на – Дону, 1973 – 98 c.
4. Данилюк, И.И. О задаче с наклонной производной. // СМЖ. Том 3, №1. 1962. –  С. 18 – 55.
5. Сабитов, И.Х. Бесконечно малые изгибания выпуклых поверхностей с краевым условием обобщённого скольжения // ДАН СССР. – 1962. – 147, №4. –  С.793 – 796 (РЖМат, 1964, 10А419).
6.Векуа, И.Н. Обобщённые аналитические функции. М.: Физматлит, 1959 – 509 с.
7. Nitsche Joachim. Beitrage zur Verbiegung zweifach zuaamtnenhangender Flachenstucke // Math. Z. – 1955. – 62, № 4. – P. 388 – 399.
8. Grotemeyer К. Р. Einige Probleme und Methoden der Flachentheorie im Grossen // Math.-phys. Semesterber. –  1964. –  10, № 2. –  P.187 – 201.
9. Онишкова, А.М. Численное решение задачи для плоской области со свободной границей [Электронный ресурс]  // «Инженерный вестник Дона», 2012, №4 (часть 1). – Режим доступа: http: // ivdon.ru /magazine/ archive/ n4p1y2012/ 1205 (доступ свободный) – Загл. с экрана. – Яз. рус.
10. Замятин, А.В., Замятина, Е.А. Алгоритм построения развёртки поверхностей [Электронный ресурс]  // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://ivdon.ru/magazine/archive/n4p2y2012/1233 (доступ свободный) – Загл. с экрана. – Яз. рус.