Расчет силовых нагрузок конструкций при испытаниях на отрыв
Аннотация
Дата поступления статьи: 28.11.2013Рассматривается расчет напряженно-деформированного состояния клееной конструкции при испытаниях на отрыв обшивки с целью определения тарировочных сил для испытательного стенда.
Ключевые слова: Метод конечных элементов, Концентрация напряжений, Обшивка, Испытания, Прогнозирование.
Клееные конструкции (например, сэндвич панели) начинают широко применяться в жилищном строительстве. Наряду с их несомненными преимуществами (высокие теплоизоляционные свойств, технологичность и экономичность строительства с их использованием и т.п.) они имеют и недостаток – неоднородность прочностных характеристик клеевого шва. Для проверки качества склейки конструкций проводят их выборочные испытания. Цель работы: рассчитать напряженно-деформированное состояние при испытаниях на отрыв элемента клееной конструкции с качественным клеевым швом для определения тарировочных сил испытательного стенда.
Задача решалась в следующей постановке. Имеется испытательный образец заданной геометрии. Необходимо выполнить расчет усилий отрыва обшивки этого образца на стенде с помощью захвата (рис. 1).
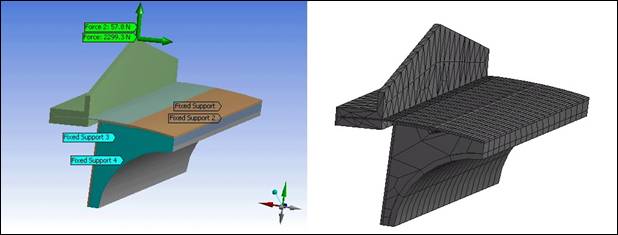
Рис. 1. – Схема испытаний и конечно-элементная модель
Модель составная. Она включает в себя стеклопластиковые обшивки, находящийся между ними пенопластовый наполнитель и стальной захват. Закрепление образца происходит по торцам, сила прикладывается к захвату. Геометрия образца, свойства его материалов, а также силовые нагрузки моделируются конечно-элементной моделью (см. рис. 1).
При расчете методом конечных элементов в классической постановке непрерывная нагрузка заменяется эквивалентными узловыми силами [4-10]. В этом случае формула для потенциальной энергии расчетной системы выражается зависимостью (1).
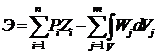 (1),
(1),
где n —количество компонентов перемещений; m — число элементов, на которые разделена система.
Первый член в уравнении (1) является линейной функцией от Zi. Из определения удельной потенциальной энергии следует, что потенциал Wj является функцией второго порядка от Z. Варьирование потенциальной энергии (1) по Zi дает систему из n уравнений относительно Z (2).
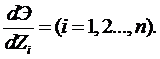 (2)
(2)
Для расчетов использован многофункциональный программный комплекс конечно-элементных расчетов ANSYS [1-3]. Разработанная методика расчета реализована в программном комплексе на языке APDL.
Таблица.
Сравнение расчетных и измеренных значений отрывного усилия.
Номер образца |
Расчетное значение отрывного усилия в Н |
Измеренное значение отрывного усилия в Н |
Абсолютная погрешность усилий в Н |
Относительная разница расчета усилий разработанной программой в % |
Примечание |
|
1 |
1830 |
2100 |
270 |
12,86 |
Верхняя обшивка |
|
1 |
1830 |
1800 |
30 |
1,67 |
Нижняя обшивка |
|
2 |
1830 |
1800 |
30 |
1,67 |
Верхняя обшивка |
|
2 |
1830 |
2000 |
170 |
8,50 |
Нижняя обшивка |
|
Среднее значение |
125 |
6,18 |
|
||
Для проверки правильности работы программного обеспечения оно проходила тестирование. Результаты сравнения расчетных и реально полученных при испытаниях на экспериментальной установке отрывных усилий показаны в табл. Видно, что расчет отрывных усилий выполнен с относительной погрешностью около 7%, что для принятых расчетных условий может быть признано удовлетворительным.
Результаты решения задачи представлены на рис. 2 и 3. Так, на рис. 2 показаны перемещения в метрах участка обшивки при проверке качества склейки в начальной зоне для одного из частных случаев (нагружения усилием в 2300 Н и обрезки обшивки на величину 45 мм).
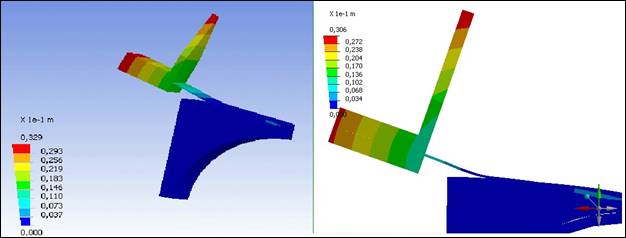
Рис. 2. – Перемещения в м участка обшивки панели при проверке качества клеевого соединения.
На рис. 3 показаны в качестве примера средние главные напряжения в Па в образце при проверке качества склейки для рассматриваемого случая.
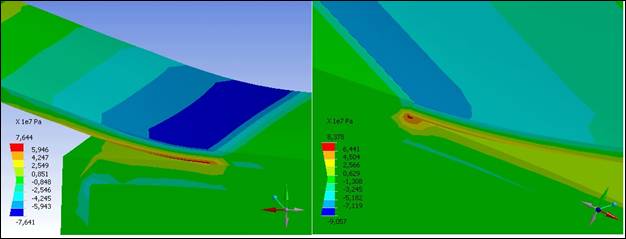
Рис. 3. – Средние главные напряжения в Па в зоне отрыва.
Таким образом, созданы конечно-элементная модель отрыва обшивки клееной конструкции от слоя наполнителя в испытательном стенде, методика и программа расчета на языке APDL напряженно-деформированного состояния образца в процессе испытаний. Это позволяет рассчитать напряженно-деформированное состояние в зоне отрыва обшивки, а также спрогнозировать поведение конструкции при отрыве обшивки в различных контрольных зонах. Модель дает среднюю относительную погрешность определения напряжений 7%. Установлено, что усилие отрыва во всех зонах не может быть одинаковым для существующей конструкции испытательного стенда, даже если качество клеевого шва неизменно. Если область отрыва условно поделить на три равные зоны, то усилия во второй зоне должны быть меньше, чем в начальной на 25 -35%, а в третьей – на 40 - 50%. Зная это соотношение, можно при испытаниях контролировать не только суммарный эффект, но и качество склейки конструкции по зонам.
Литература:
- Кадомцев М.И., Ляпин А.А., Тимофеев С.И. К вопросам построения эффективных алгоритмов расчета системы «сооружение-грунт» [Электронный ресурс] // «Инженерный вестник Дона», 2012, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2009/250 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Кадомцев М.И. Исследование деформирования частично заглубленного фундамента при гармоническом воздействии с использованием метода граничных элементов и метода конечных элементов [Электронный ресурс] // «Инженерный вестник Дона», 2012, №3. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2009/250 (доступ свободный) – Загл. с экрана. – Яз. рус.
- А. Н. Бескопыльный, М. И. Кадомцев, А. А. Ляпин. Методика исследования динамических воздействий на перекрытия пешеходного перехода при проезде транспорта [Электронный ресурс] // «Инженерный вестник Дона», 2011, №4. – Режим доступа: http://ivdon.ru/magazine/archive/n4p2y2012/1368 (доступ свободный) – Загл. с экрана. – Яз. рус.
- М. И. Кадомцев, А. А. Ляпин, Шатилов Ю.Ю. Вибродиагностика строительных конструкций [Электронный ресурс] // «Инженерный вестник Дона», 2012, №3. – Режим доступа: http://ivdon.ru/magazine/ archive/n3y2012/941 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Ляпин А.А., Селезнев М.Г., Собисевич Л.Е., Собисевич А.Л.Механико-математические модели в задачах активной сейсмологии. М.: ГНИЦ ПГК (МФ) при КубГУ Минобразования России, 1999. – 294 с.
- Варданян Г.С., Андреев В.И., Атаров Н.М., Горшков А.А. Сопротивление материалов с основами теории упругости и пластичности – М., Издательство АСВ, 1995. – 568 с.
- Литвинов В.В., Языев Б.М. Энергетический метод в форме Тимошенко-Ритца для определения критических сил осевого сжатия круговой цилиндрической оболочки. [Электронный ресурс] // «Инженерный вестник Дона», 2012, №1.– Режим доступа http://www.ivdon.ru/magazine/ archive/n1y2012/722 (доступ свободный) – Загл . с экрана. – Яз. рус.
- Дарков А.В., Шапошников Н.Н. Строительная механика: Учеб. для строит. спец. вузов - М., Высш. шк., - 1986. – 607 с.
- Andreev V.I. Minaeva A.S. Creation on the basis of the first theory of strength model equal stressed cylinder exposed to power and temperature loads. International Journal for Computational Civil and Structural Engineering. Volume 7, Issue 1, 2011. p. 71-75.
- Andreev V.I. Optimization of thick-walled shells based on solutions of inverse problems of the elastic theory for inhomogeneous bodies. Computer Aided Optimum Design in Engineering XII (OPTI XII). WIT Press. 2012, p.189-201.