Метод применения генеральной совокупности конечного объема вместо выборочной информации в расчетах усталостного ресурса деталей
Аннотация
Дата поступления статьи: 04.12.2013В статье изложен метод применения генеральной совокупности конечного объема вместо выборочной информации в расчетах усталостного ресурса деталей. Для описания статистических закономерностей использованы вероятсностные законы со сдвигом. Параметры распределения Вейбулла находятся графическим способом.
Ключевые слова: генеральная совокупность конечного объема, выборка, ресурс, расчет, усталость.
05.05.04 - Дорожные, строительные и подъемно-транспортные машины
Этот метод рассматривается для деталей с усталостными отказами, вызывающими внезапную потерю работоспособности машины (узла), что обычно сопровождается значительным экономическим ущербом, а в некоторых случаях утратой безопасной работы машины.
Выполненные нами исследования по экспериментальному определению с помощью эксплуатационных наблюдений надежности различных машин (одноковшовых экскаваторов, зерноуборочных комбайнов и др.) в период 1970-1985 г.г. [1,2,3] выявили необычную закономерность появления их отказов. Эти отказы происходили на ранних сроках эксплуатации машин.
В те годы многие детали машин рассчитывались из условия обеспечения заданного гамма – процентного ресурса [4.5]. При этом фактический ресурс оказывался меньше расчетного в несколько десятков и даже сотен раз и соответственно экономический ущерб.
На тот период времени убедительного ответа на вопрос о таком значительном расхождении у нас не было.
В последующие годы постепенно накапливалась различная информация, которая позволила отличать ресурс детали, определенный по выборке деталей в количестве n=20-50 и совокупности Nс одинаковых деталей, находящихся в эксплуатации в объеме тысяч единиц.
Далее сформулировали гипотезу о существенном отличии, например, минимальных ресурсов деталей для выборки и генеральной совокупности, находящихся в эксплуатации в объеме Nс=103-106 единиц.
Затем поставили задачу исследовать закономерность расхождения минимальных ресурсов деталей, найденных по выборке и рассчитанных для генеральных совокупностей объемом Nс=103-106 единиц.
Как видно из объема Nс, генеральная совокупность рассматривалась конечного объема в отличие от общепринятой совокупности бесконечного объема.
При этом для описания статистических закономерностей использованы вероятностные законы со сдвигом: Вейбулла – для прочности и ресурса и закон Фишера – Типпета – для действующих напряжений [6].
На рис. 1 представлена вероятностная бумага (сетка) для закона Вейбулла со сдвигом с тремя параметрами [7]. В качестве примера принято выборочное распределение ресурса деталей в интервале F(x)=0,01-0,99, т.е. для единой базы сравнения вероятностных распределений с разными относительными размахами [8].
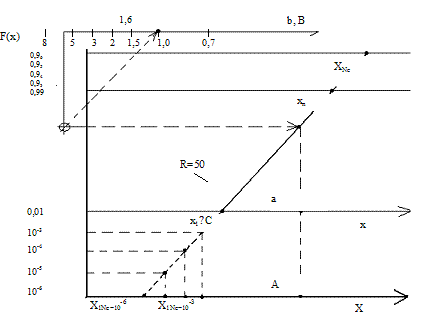
В этом примере дано:
1. Объем выборки n=50 для размаха R=50.
2. Объем совокупности Nc=103;104;105;106.
Принимаем:
- x1≈c.
- Х1≈СNc.
- а=А.
- в=В.
Имеем:
- Расхождение r= x1/Х1≈c/СNc,
Nc=103;104;105;106.
2. Размах Rc= ХNc / Х1Nc.
Здесь x1- первый член выборочного вариационного ряда;
с- сдвиг выборочного распределения вариационного ряда;
Х1- первый член вариационного ряда генеральной совокупности конечного объема;
СNc. – сдвиг распределения генеральной совокупности конечного объема;
а и А – параметры масштаба выборочного распределения генеральной совокупности конечного объема;
в и В - параметры формы выборочного распределения и генеральной совокупности конечного объема.
После нанесения точек выборочного распределения (кумуляты) построена аппроксимирующая прямая в интервале F(x)=0,01-0,99. Для корректного сравнения различных выборочных данных и приняты значения F(x)=0,01-0,99.
Параметры распределения Вейбулла а, в и с находятся графическим способом [7].
Вероятностная сетка состоит из трех частей. Верхняя часть F(x)= 0,99-0,96 является продолжением средней части выборочной прямой при F(x)=0,01-0,99 и считается распределением для генеральной совокупности конечного объема.
Нижняя часть прямой в интервале F(x)=0,01-10-6 также относится к генеральной совокупности конечного объема.
Как следует из графика, параметры а=А и в=В; x1≈c с ошибкой δ=0,1-1% и Х1Nc≈СNc с ошибкой δ=2-7% [9,10].
Выполнен расчет расхождения r минимального ресурса для генеральной совокупности конечного объема и выборки в зависимости от объема совокупности Nc и результаты представлены на рис. 2.
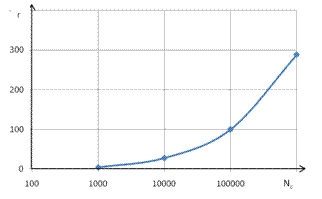
Рис. 2. Зависимость расхождения r от объема совокупности Nc
Литература:
- Касьянов В.Е. Метод определения уровня надежности одноковшовых экскаваторов [Текст] // Надежность машин.- Вып. 2. – Ростов-на-Дону: Ростовский инженерно-строительный институт, 1972. – С.98-107.
- Касьянов В.Е. Испытания экскаваторов в эксплуатации и расчет показателей их надежности на ЦВМ [Текст] //Надежность и контроль качества.- 1976.-. №6. – С.15-19.
- Касьянов В.Е., Беленький Д.М., Кубарев А.Е. Опыт анализа надежности машин по результатам длительных эксплуатационных наблюдений [Текст] //Вестник машиностроения. – 1978.- №10. – С.13-16.
- ГОСТ 27-503-81 (СТ СЭВ 2836-81). Надежность в технике. Система сбора и обработки информации. Методы оценки показателей надежности (В.Е. Касьянов, А.И. Кубарев, Д.М. Беленький и др.). [Текст]: – М.: Издательство стандартов, 1981.
- ГОСТ 27-401-84 (СТ СЭВ 4492-84). Надежность в технике. Порядок и методы контроля показателей надежности, установленных в нормативно-технической документации. Общие требования. (В.Е. Касьянов, В.Ф.Курочкин, Д.М. Беленький и др.). [Текст]: – М.: Издательство стандартов, 1984.
- W. Weibull, A statistical distribution function of wide applicability // I. Appl. Mech. 18, 3 (1951). — Pp. 293-297.
- Kapur K.C., Lamberson L.R. Reliability in Engineering Design. Departament of Industrial Engineering and Operations Research Wayne State University Detroit, Michigan 48202, 1977.
- Касьянов В.Е., М.М.Зайцева, А.А. Котесов Оценка параметров распределения Вейбулла для совокупности конечного объема Деп. В ВИНИТИ, 24.01.2012 № 21-В2012
- В.Е Касьянов М.М. Зайцева, А.А. Котесова, А.А. Котесов, С.В. Котова Расчетно-экспериментальное определение гамма-процентного ресурса стрелы одноковшового экскаватора для генеральной совокупности конечного объема [Электронный ресурс] // «Инженерный вестник Дона», 2012, №1. – Режим доступа: http:www.ivdon.ru/magazine/archive/n1y2012/624 (доступ свободный) – Загл. с экрана. – Яз. рус.
- В.Е. Касьянов А.А. Котесов, А.А. Котесова Аналитическое определение параметров закона Вейбулла для генеральной совокупности конечного объема по выборочным данным прочности стали [Электронный ресурс] // «Инженерный вестник Дона», 2012, №2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2012/804 (доступ свободный) – Загл. с экрана. – Яз. рус.