Математическое моделирование автоматизированного позиционного гидропривода целевых механизмов машин с контуром гидравлического управления повышенной эффективности
Аннотация
В работе рассматривается математическая модель автоматизированного позиционного гидропривода целевых механизмов машин оригинальной конструкции. Модель сформирована с учетом развитой структуры гидравлической системы управления привода и объединяет три подсистемы: механическую, гидравлическую и управляющую. При помощи программного пакета Matlab 2012 исследуется позиционный цикл характерный для поворотно-делительных механизмов технологического оборудования по критериям быстродействия и точности.
Ключевые слова: математическое моделирование, позиционный гидропривод, устройства управления, точность, быстродействие
Развитие машиностроительной индустрии, определяется уровнем совершенствования автоматизированного технологического оборудования (АТО) [1]. Повышение требований к быстродействию и точности их функционирования обусловливают необходимость совершенствования действующих и создания новых позиционных систем. Применение позиционных гидроприводов, в силу известных преимуществ позволяет повысить эффективность таких систем.
В позиционных гидросистемах программного регулирования, широкое применение нашли гидромеханические позиционеры - устройства организующие контур гидравлического управления [2]. Они эффективно решают задачи оптимального управления выходного звена привода, используя гидравлические линии связи (ГЛС), позволяющие регулировать потоки жидкости на входе или выходе из гидродвигателя.
Особенностью гидравлических связей ГМП, являются незначительные расходы управляющих потоков в УГЛС, что позволяет минимизировать объемы жидкости в контуре и повысить его быстродействие управляющего устройства (ГМП). Объединение нескольких исполнительных устройств в одно многофункциональное, так же повышает быстродействие и стабильность работы системы.
Возможности дальнейших исследований функционала предлагаемого схемотехнического решения ПГП, во многом зависят от качественного математического описания его гидромеханической системы.
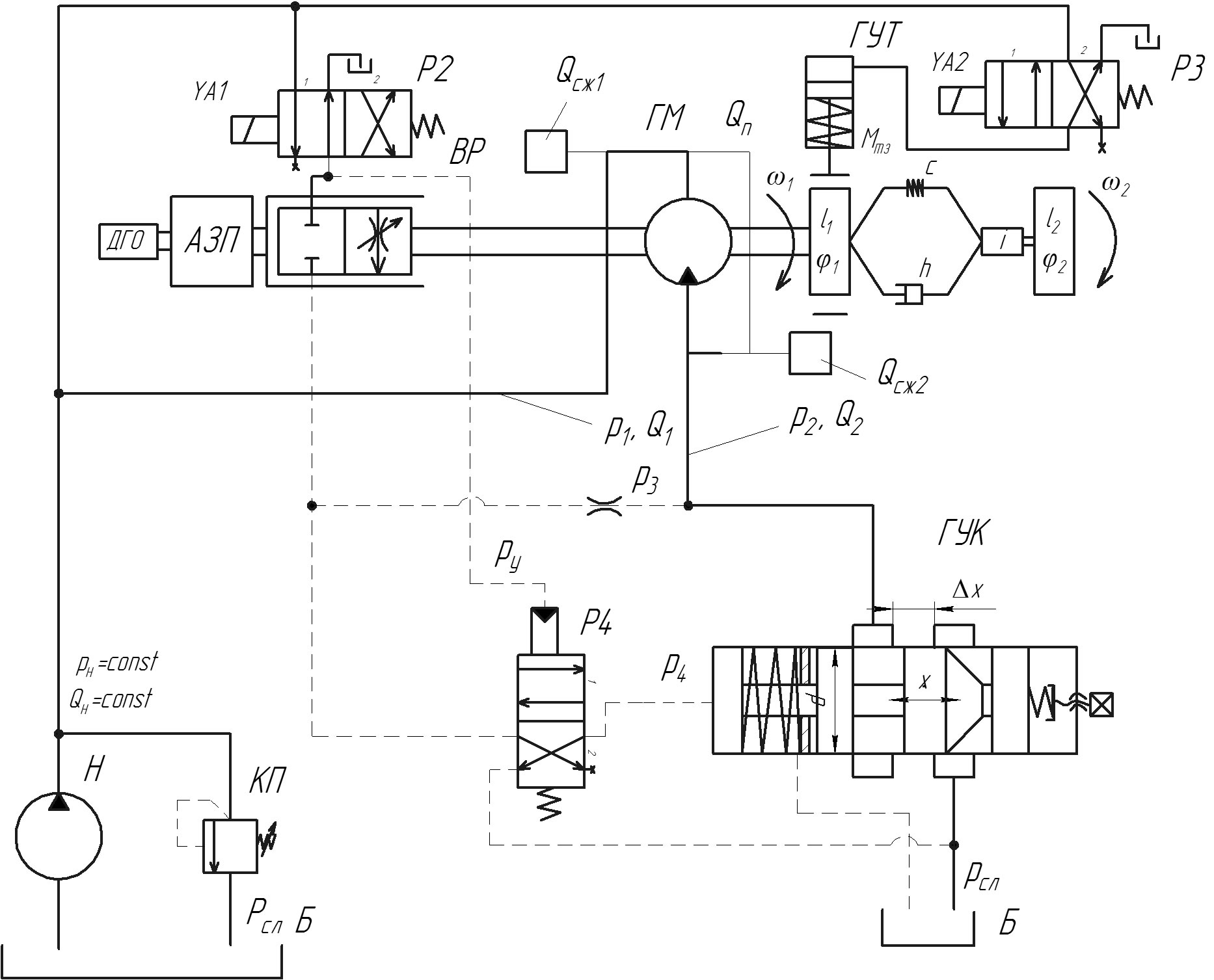
Рис.2. Расчетная схема динамической системы ПГП
При этом существенно сокращается затраты времени и средств на последующие испытания и улучшается качество рабочих процессов реальных ПГП. Для этого, на основании структурной и принципиальной гидравлических схем, разработана расчетная гидрокинематическая схема динамической системы ПГП представленная на рис.2.
Математическое описание динамических процессов протекающих в гидравлических системах осложняется особенностями поведением потока рабочей жидкости. Поэтому при формировании математической модели позиционной гидросистемы, были приняты следующие допущения:
- Механическую подсистему ГМУП в упрощённых моделях описывает одномассовая динамическая система, а в полной модели – двухмассовая;
- Утечки малы и могут быть ограничены коэффициентом утечки Ку [3];
- Трубопроводы короткие, гладкие, жесткие, что позволяет не учитывать волновые явления;
- Жесткость гидравлического силового контура Сг ниже жесткости механической подсистемы См;
- Динамические процессы протекают в окрестности точки нагрузочной характеристики привода: QН=const , pн= pклmax= const;
- Рабочая жидкость сжимаемая, капельная, в каналах присутствует нерастворённый воздух. Сосредоточенный объём сжимаемой жидкости Qсж считаем присоединенным к рабочей полости гидродвигателя;
- Принимается, что сила вязкого трения в подвижных сопряжениях пропорциональна скорости [3];
- Совмещение рабочих окон вращающегося распределителя происходит мгновенно при релейном управлении и по экспоненциальному закону - при квазирелейном управлении;
- Коэффициент расхода управляющего устройства ГУКа представлен аппроксимированной функциональной зависимостью от степени открытия золотника клапана μ=f(x) полученной экспериментально [5].
Используя основные принципы и правила математического описания динамических подсистем с механическими связями [1], гидравлических силовых и управляющих подсистем [3], составлена математическая модель, представляющая систему нелинейных дифференциальных уравнений, описывающих поведение ее подсистем.
- Уравнения движения двухмассовой механической подсистемы:
![]() ; (1)
; (1)
![]() ; (2)
; (2)
![]() ; (3)
; (3)
![]() ; (4)
; (4)
![]() (5)
(5)
![]() (6)
(6)
где I1, I2 - приведенные моменты инерции ведущих и ведомых масс, кг∙м2; φ1, φ2– координаты их угловых перемещений, рад; - момент сил гидромотора, Н∙м; , Mc1, Mc2- моменты сил сопротивления, Н∙м; M1-2 – упругий момент, Н∙м;MH – момент технологической нагрузки, Н∙м; h – коэффициент демпфирования механической подсистемы; C – коэффициент жесткости механической подсистемы; MBP– момент вращающегося распределителя, Н∙м; MT3 - тормозной момент, Н∙м; MT3(max) - максимальное значение тормозного момента, Н∙м; τ - постоянная времени нарастания тормозного момента; qM- рабочий объем гидромотора, м3; ![]() - коэффициент полноты использования периметра втулки золотника при размещении в ней окон; MT1, MT2 - моменты сухого трения, Н∙м.
- коэффициент полноты использования периметра втулки золотника при размещении в ней окон; MT1, MT2 - моменты сухого трения, Н∙м.
2. Гидравлическая силовая подсистема с дроссельным управлением описывается уравнениями баланса расходов характеризующими напорную и сливную лини [3]:
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
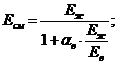 (13)
(13)
где QН - расход гидронасоса, м3/с; ![]() - расход идущий на вращение вала гидромотора, м3/с;
- расход идущий на вращение вала гидромотора, м3/с; ![]() - расход идущий на компенсацию утечек, м3/с;
- расход идущий на компенсацию утечек, м3/с; ![]() - расход идущий на перетечки рабочей жидкости, м3/с;
- расход идущий на перетечки рабочей жидкости, м3/с; ![]() - расход идущий на компенсацию деформируемого объема жидкости в полостях гидромотора и подводящих каналах, м3/с; QГУК- расход проходящий через гидроуправляемый клапан, м3/с; rу, rп, - коэффициенты утечки и перетечки; Eв, Eж - модули объемной упругости жидкости и воздуха; αB – коэффициент учитывающий содержание воздуха в жидкости; Wiгл – объем i-го участка гидролиний соответственно м3;
- расход идущий на компенсацию деформируемого объема жидкости в полостях гидромотора и подводящих каналах, м3/с; QГУК- расход проходящий через гидроуправляемый клапан, м3/с; rу, rп, - коэффициенты утечки и перетечки; Eв, Eж - модули объемной упругости жидкости и воздуха; αB – коэффициент учитывающий содержание воздуха в жидкости; Wiгл – объем i-го участка гидролиний соответственно м3; ![]() - приращение давления в напорной полости гидромотора.
- приращение давления в напорной полости гидромотора.
Зависимость дросселирования расхода рабочей жидкости QЗ через окна золотников гидрораспределителей [4], от изменения их проходного сечения и перемещения золотника ![]() при перепаде давлений
при перепаде давлений ![]() определяется с помощью выражения:
определяется с помощью выражения:
![]() ; (14)
; (14)
где ![]()
![]() - удельные (отнесенные к единице перемещения золотника) проводимости окон, открытых при смещении золотника от среднего положения;
- удельные (отнесенные к единице перемещения золотника) проводимости окон, открытых при смещении золотника от среднего положения;
Преобразуя уравнения (7), (8) и выполнив подстановку значений расходов, получим уравнения характеризующие изменения давлений для напорной и сливной гидролиний:
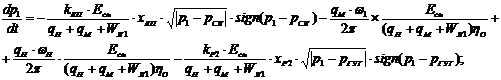 (15)
(15)
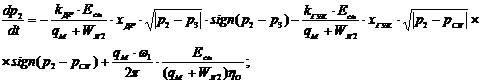 (16)
(16)
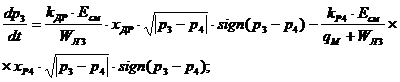 (17)
(17)
![]() (18)
(18)
3.Управляющая подсистема реализуется контуром гидравлического управления КГУ, описываемым подмоделями ВР, движением золотника ГУКа и управляющими гидролиниями.
3.1Уравнение движения золотника Р4, управляющего ГУК:
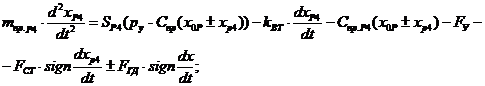 (19)
(19)
где ![]() - приведенная масса золотника распределителя, Н∙с2/м-4;
- приведенная масса золотника распределителя, Н∙с2/м-4; ![]() - сила сухого трения, Н;
- сила сухого трения, Н; ![]() – давление управления распределителя, Па;
– давление управления распределителя, Па; ![]() - коэффициент вязкого трения;
- коэффициент вязкого трения; ![]() - жесткость пружины распределителя, Н/м;
- жесткость пружины распределителя, Н/м; ![]() - реакция силы упоров, Н;
- реакция силы упоров, Н; ![]() - предварительная деформация пружины распределителя, м;
- предварительная деформация пружины распределителя, м; ![]() - перемещение золотника распределителя, м.
- перемещение золотника распределителя, м.
3.2 Уравнение движения золотника гидроуправляемого клапана:
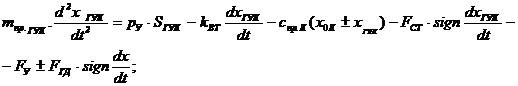 (20)
(20)
где ![]() - приведенная масса золотника клапана,Н∙с2/м-4;
- приведенная масса золотника клапана,Н∙с2/м-4; ![]() – давление управления клапана, Па;
– давление управления клапана, Па; ![]() – жесткость пружины клапана, Н/м;
– жесткость пружины клапана, Н/м; ![]() – перемещение золотника клапана, м;
– перемещение золотника клапана, м; ![]() – предварительная деформация пружины клапана, м; SГУК – эффективная площадь золотника ГУКа, м2.
– предварительная деформация пружины клапана, м; SГУК – эффективная площадь золотника ГУКа, м2.
3.3 Уравнение управляющего давления распределителя Р4:
![]() (21)
(21)
где ![]() и
и ![]() - объем гидролиний и гидроаппарата соответственно, м3;
- объем гидролиний и гидроаппарата соответственно, м3; ![]() - перемещение запорно-регулирующего элемента соответствующего гидроаппарата, м;
- перемещение запорно-регулирующего элемента соответствующего гидроаппарата, м; ![]() - эффективная площадь запорно-регулирующего элемента соответствующего гидроаппарата, м2;
- эффективная площадь запорно-регулирующего элемента соответствующего гидроаппарата, м2; ![]() – давление соответствующего участка гидропривода, Па;
– давление соответствующего участка гидропривода, Па; ![]() - модуль объемной упругости смеси жидкости и воздуха, Па;
- модуль объемной упругости смеси жидкости и воздуха, Па;
Математическая модель системы ПГП исследовалась с использованием программного пакета Matlab 2011a и её подсистемы модульного моделирования динамических процессов simulink. При решении, применяли прямой численный метод Рунге-Кутта и Эйлера с постоянным шагом интегрирования равным 0,00001. При этом принятые начальные условия, параметры контура гидравлического управления и управляющие воздействия (хi), имели функциональную зависимость от координаты выходного звена (![]() ).
).
Реализация и решение системы дифференциальных уравнений описывающих динамическую систему позиционного гидропривода, в программе Matlab, выполнялось в соответствии с алгоритмом:
1. Составление вычислительного блока для решения одномассовой матмодели позиционного гидропривода.
2. Введение в модель, подмодели гидравлического силового контура в составе которого участвуют гидрораспределители ВР, Р2 и Р3 с релейной схемой включения (учитывая реальное время срабатывания tср=0,002…0,003с) [2].
3. Введение в модель, подмодели гидравлического контура управления с гидролининиями связи – распределителя Р4, с квази-релейной схемой переключения.
4. Интеграцию в КГУ, модели гидравлического устройства управления – ГУКа, с аппроксимацией зависимости μ=f(x)соответствующейреальным гидродинамическим процессам [3], полученную с учетом динамических характеристик измерительных устройств [4].
5. Выбор метода решения системы дифференциальных уравнений математической модели и соответствующего размера шага.
Исследования проводились при различных диапазонах функционирования гидромеханической системы привода. Был определен базовый режим работы, характерный для большинства поворотно-делительных механизмов АТО. Оценка погрешностей и статистическая обработка полученных численных данных по известной методике [5].
В результате выполненной отладки и апробации вычислительных блоков программы, реализованной в подсистеме Simulink, получены осциллограммы зависимостей выходных параметров: φ, ω – механической подсистемы, а так же задающих воздействий– xГУК и xР2, xP4 - перемещения управляющих элементов КГУ.
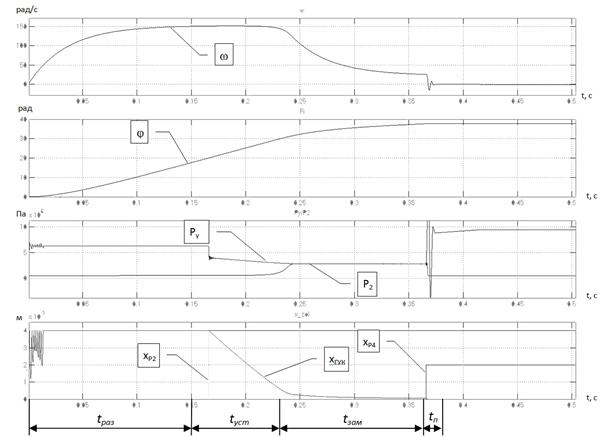
Рис. 3. Результаты моделирования динамической системы ПГП:
φ , ω – радиальные перемещение и скорость; Pу – давление управления; P2 – давление сливной магистрали ГМ; xГУК – перемещение золотника ГУКа; xР2 – перемещение золотника Р2; xР4 – перемещение золотника Р4
Движение одномассовой механической подсистемы, характеризует фазовый портрет координаты перемещения выходного звена (рис.3). Движение приведенных масс I, в момент завершения процесса позиционирования, сопряжено с колебаниями (0,37 c), которые благодаря включению гидромеханического тормозного устройства – гасятся, в области Δφ.
Точность позиционирования ![]() определяли выражением
определяли выражением ![]() , где
, где ![]() – положительный выбег гидромотора,
– положительный выбег гидромотора, ![]() – его рассеяние, обусловленное влиянием случайных факторов.
– его рассеяние, обусловленное влиянием случайных факторов.
Табл. Результаты сравнения ПГП с различной структурой КГУ
|
Устройство позиционер |
Ру, |
nгм, |
nоу, |
Мгм, |
φгм, |
Δφгм, |
Δφоу, |
tp, |
Σtт, |
|
Гидрозамок |
- |
140 |
11,6 |
10 |
0,345 |
0,052 |
0,004 |
0,055 |
0,07 |
|
МФУУ |
1,7 |
0,215 |
0,01 |
0,003 |
0,42 |
0,54 |
|||
|
3 |
0,108 |
0,029 |
0,002 |
0,46 |
0,41 |
||||
|
ГУКП |
3 |
150 |
12,5 |
10 |
0,102 |
0,023 |
0,0017 |
0,39 |
0,37 |
|
6,3 |
0,103 |
0,02 |
0,0015 |
0,042 |
0,27 |
По результатам моделирования, при заданных режимах ip, iу, nгм, Мгм очевидна эффективность процесса позиционирования с применением ГУКП. В среднем, точность позиционирования повышается ~ на 40 %, а быстродействие на 33%, по сравнению с конкурирующими решениями на основе МФУУ (см. Табл.), что подтверждает эффективность предлагаемого схемотехнического решения.
Литература
1. Кудинов В.А. Динамика станков. – М.: Машиностроение, 1967. – 359с.
2. Сидоренко В.С., Полешкин М.С. Многофункциональное гидромеханическое устройство позиционирования целевых механизмов станочных систем повышенного быстродействия и точности / Вестник ДГТУ. - 2009. –Т.9. – Спец. вып.
3. Попов Д.Н. Механика гидро- и пневмоприводов: учеб. для вузов. – М.:Изд-во МГТУ им Н.Э.Баумана,2001.-320с.,ил.
4. Иосифов В.П. Имитационный подход к проблеме определения динамических характеристик средств измерений / Инженерный Вестник Дона [Электронный ресурс]. – Ростов-на-Дону: Ростовское региональное отделение РИА – №4, 2010. – Шифр Информрегистра: 0421100096–URL: http://www.ivdon.ru/magazine/archive/n4y2010/308/-5с
5. Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке. Методы обработки данных.–М.: Мир, 1980. – 602 с.