Определение действующего напряжения в стреле одноковшового экскаватора
Аннотация
В данной работе предлагается метод определения параметров распределения Фишера-Типпета генеральной совокупности конечного объема (Ас, Вс, Сс) по выборочным данным средневзвешенных напряжений. При этом рекомендуется использовать средние значения параметров Ас, Вс, Сс полученные при многократном моделировании.
Ключевые слова: выборочные данные, напряжение, распределение Фишера-Типпета, совокупность, моделирование
05.05.04 - Дорожные, строительные и подъемно-транспортные машины
Актуальной задачей машиностроительной отрасли остается повышение эффективности техники. Одним из основных показателей надежности (долговечности) является усталостный ресурс машины (детали). Для его получения необходимо определить действующее напряжение в опасном сечении детали при эксплуатации. При этом построение распределения средневзвешенных напряжений [1] в реальных условиях трудоемкая и дорогостоящая задача, так как требуется провести тензометрирование однотипных деталей на представительной партии машин (например, одноковшовых экскаваторов), которые обычно территориально рассредоточены. В данной ситуации на первый план выходят задачи совершенствования и разработки новых методов получения параметров распределения генеральной совокупности конечного объема (совокупности) с помощью выборочных данных.
В данной работе предлагается метод определения параметров совокупности распределения Фишера-Типпета (ФТ) Ас, Вс, Сс по выборочным данным средневзвешенных напряжений, алгоритм которого представлен на рис.1.

Рис. 1. Алгоритм получения параметров распределения ФТ Ас, Вс, Сс для совокупности средневзвешенных напряжений, где: σсвi – вариационный ряд средневзвешенных напряжений; а, b, с – выборочные параметры распределения ФТ; n – объем выборки; Г(–) – гамма-функция; Uγ – квантиль нормального распределения; γ – вероятность, соответствующая нормальному распределению.
Известно [1], что для аппроксимации данных по нагруженности применяется распределение ФТ 2-го порядка:
функция распределения
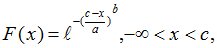
плотность распределения
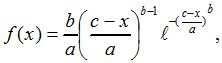
где а, b, c – параметры распределения ФТ
По принципу соответствия выборки и совокупности конечного объема (репрезентативности выборки) параметры форм выборки b и совокупности Вс будут равны, т.е. Вс= b [2].
По данному алгоритму проведен вычислительный эксперимент. Из моделированной совокупности значений средневзвешенных напряжений σсвi в опасном сечении стрелы экскаватора, с параметрами распределения Ac=33,05; Bc=3,03; Cc=69,6 объема Nс=104 получены выборки объемом n=50 в количестве m=50 штук. Определены параметры распределения совокупности Асγi, Всγi, Ссγi для γ = 0,95 – 0,95 где i=1,…,m.
Найдены максимальные Ссmax, Aсmax; минимальные Ссmin, Aсmin и средние Ссср, Aсср значения параметров. Вычислены погрешности  их определения относительно параметров исходной совокупности. Результаты представлены в табл.1.
их определения относительно параметров исходной совокупности. Результаты представлены в табл.1.
Построены графики плотности распределения ФТ выборочных данных и совокупности (рис.2)
Таблица 1
Параметры распределения Фишера – Типпета для совокупности и погрешности δ% их определения
| γ | 0,95 | 0,99 | 0,93 | 0,94 | 0,95 |
| Ссmin | 64,19 | 65,47 | 66,91 | 68,09 | 69,12 |
| δ% | 8,4 | 6,3 | 4,0 | 2,2 | 0,7 |
| Ссср | 71,49 | 72,86 | 74,41 | 75,68 | 76,78 |
| δ% | 2,4 | 4,3 | 6,3 | 7,8 | 9,1 |
| Ссmax | 77,32 | 78,90 | 80,68 | 82,14 | 83,40 |
| δ% | 9,9 | 11,8 | 13,7 | 15,3 | 16,5 |
| Aсmin | 26,31 | 27,67 | 29,22 | 30,48 | 31,59 |
| δ% | -25,63 | -19,43 | -13,11 | -8,42 | -4,63 |
| Aсср | 32,91 | 34,44 | 36,18 | 37,59 | 89,91 |
| δ% | -1,3 | 3,1 | 7,9 | 11,4 | 14,2 |
| Aсmax | 38,44 | 40,12 | 42,00 | 43,55 | 44,90 |
| δ% | 14,0 | 17,6 | 21,3 | 24,1 | 26,4 |
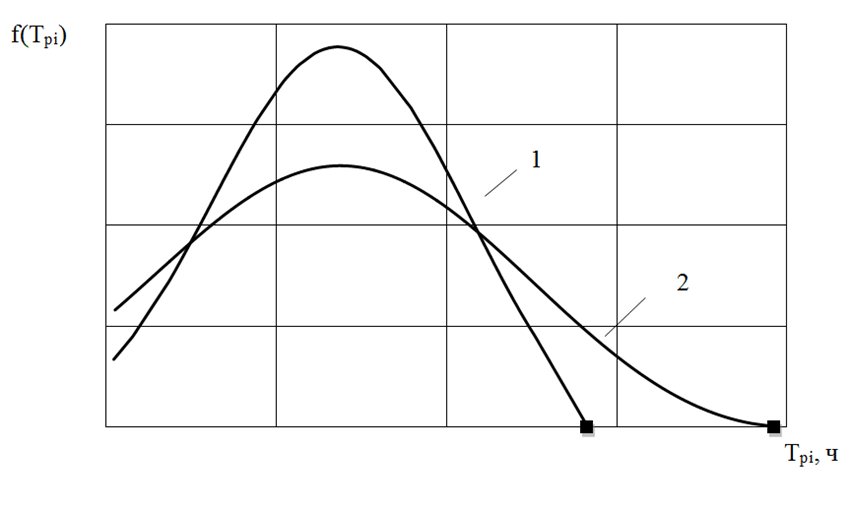
Рис. 2. Плотности распределения Фишера-Типпета выборочных данных (1) и совокупности (2) средневзвешенных напряжений
Таким образом, предлагаемый метод позволяет получить параметры распределения Фишера-Типпета генеральной совокупности конечного объема средневзвешенных напряжений. При этом рекомендуется использовать средние при многократном моделировании параметры, так как погрешность в данном случае минимальная и составляет для Ссср =2,4 – 9,1%, а для Aсср =1,3 – 14,2 % .
Библиографический список:
-
Справочник по надежности / под ред. Левина Б.Р. Мир, 1969. – 3том.
-
Касьянов В.Е., Зайцева М.М., Котесова А.А., Котесов А.А. Определение параметров распределения закона Вейбулла для совокупности конечного объема// Деп. в ВИНИТИ, 24.01.2012 № 21 – В 2012.