Энергетический метод в форме Тимошенко-Ритца для определения критических сил осевого сжатия круговой цилиндрической оболочки.
Аннотация
Энергетическим методом в форме Тимошенко-Ритца решена задача устойчивости круговой цилиндрической оболочки при равномерном осевом сжатии. Рассмотрена осесимметричная форма выпучивания оболочки в процессе потери устойчивости и осесимметричное исходное состояние, а так же осесимметричное докритическое состояние в процессе обжатия. Полученное решение в точности согласуется с решением Лоренца-Тимошенко известным как классическое.
Ключевые слова: Оболочка, устойчивость, энергия, работа, выпучивание.Ключевые слова:
Энергетическим методом в форме Тимошенко-Ритца решена задача устойчивости круговой цилиндрической оболочки при равномерном осевом сжатии. Рассмотрена осесимметричная форма выпучивания оболочки в процессе потери устойчивости и осесимметричное исходное состояние, а так же осесимметричное докритическое состояние в процессе обжатия. Полученное решение в точности согласуется с решением Лоренца-Тимошенко известным как классическое.
Рассмотрим цилиндрическую оболочку радиуса ![]() и высотой
и высотой ![]() , свободно опирающуюся на плоскость и нагруженную по верхнему краю равномерно распределенной погонной нагрузкой
, свободно опирающуюся на плоскость и нагруженную по верхнему краю равномерно распределенной погонной нагрузкой ![]() (рис.1.). Предполагаем возможность свободного расширения оболочки в радиальном направлении. Тогда исходное докритическое состояние рассматриваемой оболочки будет осесимметричным при отсутствии бесконечно малых изгибаний и при удовлетворении тангенциальным граничным условиям. Исследуем осесимметричную форму потери устойчивости оболочки, используя для этого энергетический критерий устойчивости в форме Тимошенко-Ритца.
(рис.1.). Предполагаем возможность свободного расширения оболочки в радиальном направлении. Тогда исходное докритическое состояние рассматриваемой оболочки будет осесимметричным при отсутствии бесконечно малых изгибаний и при удовлетворении тангенциальным граничным условиям. Исследуем осесимметричную форму потери устойчивости оболочки, используя для этого энергетический критерий устойчивости в форме Тимошенко-Ритца.
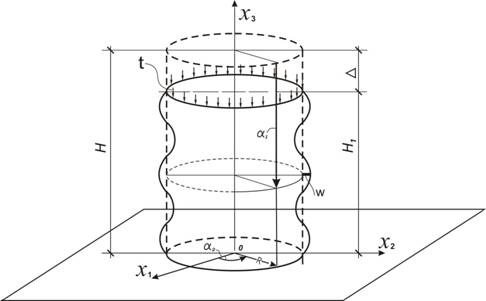
Рис.1.
В силу малости различий высоты оболочки перед выпучиванием ![]() и после выпучивания
и после выпучивания ![]() будем их отождествлять. Об изменение же этой высоты в процессе обжатия оболочки вообще можно было бы не говорить, так как это изменение является величиной еще более высокого порядка малости.
будем их отождествлять. Об изменение же этой высоты в процессе обжатия оболочки вообще можно было бы не говорить, так как это изменение является величиной еще более высокого порядка малости.
Деформация оболочки до выпучивания (в процессе обжатия) характеризуется ее мембранными компонентами: осевой деформацией ![]() и окружной деформацией
и окружной деформацией ![]() причем
причем
![]()
При осесимметричной форме потери устойчивости цилиндрической оболочки её поведение вполне определяется радиальным перемещением точек срединной поверхности ![]() , для которого можно принять тригонометрический ряд
, для которого можно принять тригонометрический ряд
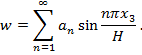 (1)
(1)
Сближение краев оболочки после выпучивание можно определить по известной формуле
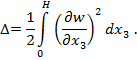 |
(2) |
Деформация оболочки после выпучивания характеризуется кроме мембранных компонент ![]() и
и ![]() изменением кривизны её срединной поверхности в осевом направлении
изменением кривизны её срединной поверхности в осевом направлении ![]() , которая подсчитывается по формуле
, которая подсчитывается по формуле
![]()
Таким образом, можно говорить о компонентах добавочной деформации, появляющейся в результате потери устойчивости оболочки. Найдем эти компоненты.
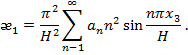
Мембранные компоненты добавочной деформации ![]() и
и ![]() определим из геометрических соображений, используя рис.2, где показано поперечное сечение цилиндрической оболочки до и после выпучивания.
определим из геометрических соображений, используя рис.2, где показано поперечное сечение цилиндрической оболочки до и после выпучивания.
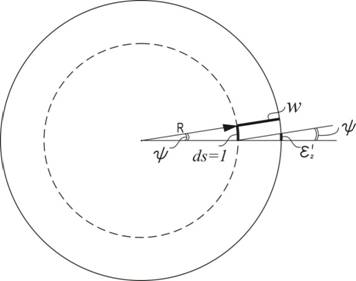
Рис.2
Из подобия криволинейных треугольников имеем
![]()
Тогда
![]()
Потенциальная энергия деформации, сопровождающей выпучивание оболочки при потере устойчивости приведена в [1] и имеет вид:
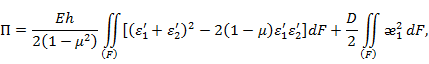
где ![]() коэффициент Пуассона;
коэффициент Пуассона;
![]() модуль упругости материала оболочки;
модуль упругости материала оболочки;
![]() толщина оболочки;
толщина оболочки;
![]()
Переходя от интегралов по площади к интегралам по высоте оболочки, получим
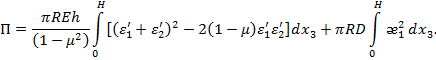
Подставляя в первый интеграл вместо ![]() и
и ![]() их выражения через радиальное перемещение
их выражения через радиальное перемещение ![]() , после упрощений получим:
, после упрощений получим:
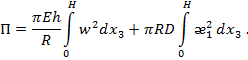
Работа внешних сил представляем собой работу равномерно распределенной нагрузки ![]() , совершаемую в процессе сближения краев оболочки на величину
, совершаемую в процессе сближения краев оболочки на величину ![]() , то есть
, то есть
![]()
или с учетом (2)
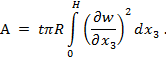
Полная потенциальная энергия системы определяется выражением
![]()
поэтому в данном случае будет
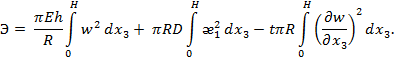
Используя принцип минимума полной потенциальной энергии системы, можно записать
![]()
или в более развернутом виде
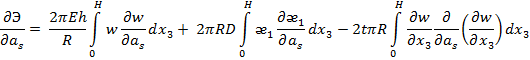
![]()
Здесь
![]()
![]()
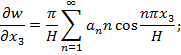
![]()
Производя все необходимые в подынтегральных выражениях подстановки и объединив первые два интеграла, получим
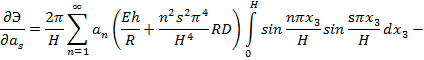
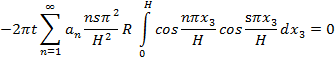
![]()
Имеющие здесь место интегралы обладают следующим свойством:
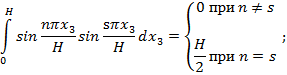
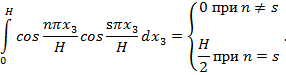
![]()
![]() то есть
то есть
![]()
![]()
В этом случае
![]()
![]()
или
![]()
![]() .
.
![]()
![]()
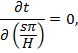
которое дает
![]()
Отсюда
![]()
и далее
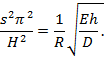
С учетом последнего из выражения для![]() после несложных преобразований получим критическую нагрузку
после несложных преобразований получим критическую нагрузку
(3) |
Полученное решение задачи в точности согласуется с решением Лоренца-Тимошенко, известным как классическое![]() .
.
Следует отметить, что данное решение справедливо при любой длине оболочки. Это объясняется принятым характером исходного состояния, то есть при отсутствии даже бесконечно малых изгибаний и тангенциальных граничных условиях.
Нельзя, однако, утверждать, что полученное здесь решение определяет вообще наименьшую критическую нагрузку. Оно определяет таковую лишь в пределах реализации осесимметричной формы потери устойчивости цилиндрической оболочки. Для длинных же оболочек следует ожидать реализации не осесимметричной потери устойчивости. Поэтому для полного решения задачи следовало бы снять ограничения о симметрии, что вообще говоря, выходит за рамки, намеченные в этой работе.
Литература
-
1.Огибалов П.М., Колтунов М.А. Оболочки и пластины. – М., Изд-во МГУ, 1969
2.Тимошенко С.П. Устойчивость стержней, пластин и оболочек.– М., Изд-во «Наука», 1971.