Построение сложных классификаторов для объектов в многомерных пространствах
Аннотация
Дата поступления статьи: 15.04.2013Статья посвящена актуальной проблеме построения классификаторов объектов, задаваемых точками в многомерном пространстве значений признаков.Принцип линейной нормальной классификации объектов в многомерных пространствах признаков может быть использован для построения классификаторов в случае множеств сложной структуры, неразделимые в общем случае одной гиперплоскостью. В таких случаях предложено использовать совокупность иерархически связанных нормальных разделяющих гиперплоскостей, которая названа иерархическим нормальным классификатором.
Ключевые слова: распознавание, классификация, пространство признаков, геометрический метод
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
Принцип линейной нормальной классификации объектов в многомерных пространствах признаков может быть использован для построения классификаторов в случае множеств сложной структуры, неразделимые в общем случае одной гиперплоскостью. В таких случаях предложено использовать совокупность иерархически связанных нормальных разделяющих гиперплоскостей, которая названа иерархическим нормальным классификатором (ИНК).
Для каждого распознаваемого множества![]() ИНК содержит совокупность нормальных гиперплоскостей
ИНК содержит совокупность нормальных гиперплоскостей ![]() , заданных множествами их коэффициентов
, заданных множествами их коэффициентов ![]() . Все гиперплоскости
. Все гиперплоскости ![]() разделены на слои. Число слоев обозначим
разделены на слои. Число слоев обозначим ![]() . Число гиперплоскостей в слое с номером s обозначим через
. Число гиперплоскостей в слое с номером s обозначим через ![]() . Набор коэффициентов гиперплоскости из совокупности
. Набор коэффициентов гиперплоскости из совокупности ![]() в слое с номером s, имеющей номер k, будем обозначать как
в слое с номером s, имеющей номер k, будем обозначать как![]() . Для упрощения выражений наряду с вектором координат точек
. Для упрощения выражений наряду с вектором координат точек ![]() будем использовать однородные векторы
будем использовать однородные векторы ![]() , у которых на начальной позиции к
, у которых на начальной позиции к ![]() добавлена единица.
добавлена единица.
Алгоритм проверки включения заданной точки пространства ![]() в множество
в множество![]() с использованием ИНК, содержащего
с использованием ИНК, содержащего ![]() слоев, в каждом из которых (с номером s) хранится
слоев, в каждом из которых (с номером s) хранится ![]() гиперплоскостей
гиперплоскостей ![]() , заключается в том, что производится перебор по всем слоям s ИНК от 1 до
, заключается в том, что производится перебор по всем слоям s ИНК от 1 до ![]() . Для каждого слоя s последовательно производится подстановка координат однородного вектора
. Для каждого слоя s последовательно производится подстановка координат однородного вектора![]() , во все уравнения плоскостей слоя. При получении первого же неотрицательного значения в скалярном произведении
, во все уравнения плоскостей слоя. При получении первого же неотрицательного значения в скалярном произведении
![]() (1)
(1)
делается вывод о вхождении точки ![]() в множество
в множество![]() , выходим из алгоритма с ответом:
, выходим из алгоритма с ответом: ![]() . Если же во всех скалярных произведениях для гиперплоскостей первого слоя выполняется условие
. Если же во всех скалярных произведениях для гиперплоскостей первого слоя выполняется условие ![]() , то проверку необходимо продолжать в следующем слое. После подстановки в условие (1) коэффициентов гиперплоскостей последнего слоя Li проверку завершаем. Если при этом ни одного неотрицательного значения в скалярных произведениях
, то проверку необходимо продолжать в следующем слое. После подстановки в условие (1) коэффициентов гиперплоскостей последнего слоя Li проверку завершаем. Если при этом ни одного неотрицательного значения в скалярных произведениях![]() не было получено, то отсюда следует, что:
не было получено, то отсюда следует, что:![]() .
.
Применение ИНК позволяет решать задачу разделения множеств для совокупностей множеств любой структуры, имеющих сложное относительное расположение в пространстве признаков.ИНК каждого множества ![]() предложено определять путем его разделения с остальными множествами. Поскольку с точки зрения включения точек в
предложено определять путем его разделения с остальными множествами. Поскольку с точки зрения включения точек в ![]() все другие множества одинаковы, то после объединения их можно считать одним множеством. Таким образом, для практического решения задачи построения ИНК отдельного множества достаточно разработать алгоритм только для пары множеств.
все другие множества одинаковы, то после объединения их можно считать одним множеством. Таким образом, для практического решения задачи построения ИНК отдельного множества достаточно разработать алгоритм только для пары множеств.
Для решения задачи построения ИНК отдельного множества в алгоритме для пары множеств предложено использовать две дополнительные операции по разделению множеств – отсечение и бинарную кластеризацию.
Если для пары множеств![]() и
и ![]() не существует единой нормальной разделяющей гиперплоскости, то предлагается выполнить разделение
не существует единой нормальной разделяющей гиперплоскости, то предлагается выполнить разделение ![]() и
и ![]() путем повторного применения принципа нормального разделения не к целым множествам, а к их частям.
путем повторного применения принципа нормального разделения не к целым множествам, а к их частям.
Нормальную по отношению к межосевому вектору ![]() гиперплоскость, которая отделяет все точки из
гиперплоскость, которая отделяет все точки из ![]() и не содержит точек из
и не содержит точек из ![]() , назовем отсекающей для множества
, назовем отсекающей для множества ![]() ,а подмножество
,а подмножество![]() - отсекаемым. Аналогично вводится отсекающая плоскость для множества
- отсекаемым. Аналогично вводится отсекающая плоскость для множества ![]() ,. Практически построение отсекающих плоскостей производится перебором массива расстояний их точек до некоторой пробной нормальной плоскости.
,. Практически построение отсекающих плоскостей производится перебором массива расстояний их точек до некоторой пробной нормальной плоскости.
Применение только одного нормального разделения и отсечения подмножеств в общем случае недостаточно для решения задач нормальной классификации множеств сложного вида – как для вложенных множеств, так и в тех случаях, когда отсекаемые множества пусты. Для преодоления данных затруднений предложено дополнительно применять близкое по назначению к кластеризации разбиение одного из множеств ![]() и
и ![]() на две части. Его задача - выделение пары максимально сгруппированных подмножеств. Назовем такой способ разбиения и получаемые подмножества для краткости бинарным. Обозначим бинарные подмножества выделенного множества А через
на две части. Его задача - выделение пары максимально сгруппированных подмножеств. Назовем такой способ разбиения и получаемые подмножества для краткости бинарным. Обозначим бинарные подмножества выделенного множества А через ![]() .
.
Поскольку качество кластеризации повышается с уменьшением радиусов кластеров R1,R2 и увеличением межцентрового расстояния ![]() между ними, то в качестве критерия сгруппированности подмножеств
между ними, то в качестве критерия сгруппированности подмножеств ![]() и
и ![]() предложено использовать ранее введенную степень разделимости подмножеств
предложено использовать ранее введенную степень разделимости подмножеств ![]() , а в качестве меры его оптимальности - максимум. Условие оптимальности получаемого разбиения
, а в качестве меры его оптимальности - максимум. Условие оптимальности получаемого разбиения![]() принимает вид:
принимает вид:
![]() /(
/(![]() , (2)
, (2)
В общем случае глобальный экстремум задачи (2) может достигаться не на единственной паре возможных подмножеств ![]() . Точное ее решение можно найти перебором всех возможных вариантов разбиения множества на пары непустых подмножеств
. Точное ее решение можно найти перебором всех возможных вариантов разбиения множества на пары непустых подмножеств ![]() и вычислением для них значения
и вычислением для них значения ![]() с последующим сравнением полученного значения с текущим максимумом
с последующим сравнением полученного значения с текущим максимумом ![]() . Обозначим через
. Обозначим через ![]() число точек в исходном множестве
число точек в исходном множестве ![]() .
.
Практически точный переборный алгоритм решения задачи (2) реализуется перебором всех кодовых чисел k из отрезка![]() , описывающих все различные варианты разбиения
, описывающих все различные варианты разбиения ![]() на подмножества
на подмножества ![]() . По k формируются
. По k формируются ![]() и производится вычисление значения критерия
и производится вычисление значения критерия ![]() . В качестве оптимального принимается тот вариант разбиения, при котором достигается максимум значений
. В качестве оптимального принимается тот вариант разбиения, при котором достигается максимум значений ![]() .
.
Принимая в качестве характерного параметра задачи число точек ![]() в разбиваемом множестве А, получим, что сложность точного переборного алгоритма равна
в разбиваемом множестве А, получим, что сложность точного переборного алгоритма равна ![]() , т.е. является экспоненциальной. Поэтому использование точного алгоритма решения задачи бинарной кластеризации для обычных вычислительных устройств возможно только при относительно небольших разделяемых множествах, примерно для значений
, т.е. является экспоненциальной. Поэтому использование точного алгоритма решения задачи бинарной кластеризации для обычных вычислительных устройств возможно только при относительно небольших разделяемых множествах, примерно для значений ![]() .
.
Практически размер разделяемых множеств ![]() может быть достаточно большим. Также в процессе решения общей задачи классификации данный алгоритм может применять десятки раз. Поэтому основной задачей точного алгоритма является решение тестовых задач, а на практике для бинарной классификации необходимо использовать приближенные алгоритмы, сочетающие более низкую сложность с получением решений, достаточно близких значений критерия качества. У данных алгоритмов условие глобальной оптимальности заменяется локальной оптимальностью, при которой получаемое решение может быть лучшим только для ограниченного подмножества общей области поиска.
может быть достаточно большим. Также в процессе решения общей задачи классификации данный алгоритм может применять десятки раз. Поэтому основной задачей точного алгоритма является решение тестовых задач, а на практике для бинарной классификации необходимо использовать приближенные алгоритмы, сочетающие более низкую сложность с получением решений, достаточно близких значений критерия качества. У данных алгоритмов условие глобальной оптимальности заменяется локальной оптимальностью, при которой получаемое решение может быть лучшим только для ограниченного подмножества общей области поиска.
Изучение оптимальных решений задачи бинарной кластеризации множеств показывает, что в получаемых оптимальных подмножествах всегда присутствуют по одной точке из какой-либо или из нескольких пар максимально удаленных точек.
Поэтому построение бинарных подмножеств предложено начать с размещения в них точек, между которыми достигается максимальное расстояние. Представители выделенной пары максимально удаленных точек, размещаемые вначале для подмножеств![]() , обозначим через
, обозначим через ![]() ,
,![]() и назовем начальными. Максимальная удаленность точек
и назовем начальными. Максимальная удаленность точек ![]() и
и![]() позволяет сделать ряд заключений о местоположении всех других точек А и их возможном включении в подмножества
позволяет сделать ряд заключений о местоположении всех других точек А и их возможном включении в подмножества ![]() и
и ![]() . Они могут находиться только внутри пересечения сфер радиусов
. Они могут находиться только внутри пересечения сфер радиусов![]() с центрами в
с центрами в![]() ,
,![]() и
и![]() .Наиболее простой вариант разделения реализуется с использованием нормальной гиперплоскости pn, проходящей через среднюю точку
.Наиболее простой вариант разделения реализуется с использованием нормальной гиперплоскости pn, проходящей через среднюю точку ![]() вектора (
вектора (![]() ,
,![]() ,) (рис.1). Для точек этой гиперплоскости (
,) (рис.1). Для точек этой гиперплоскости (![]() ) выполняется условие
) выполняется условие ![]() . Вводя для краткости прямое и обратное отношения
. Вводя для краткости прямое и обратное отношения ![]() и
и ![]() представим условие (
представим условие (![]() ) в виде:
) в виде:
![]() .
.
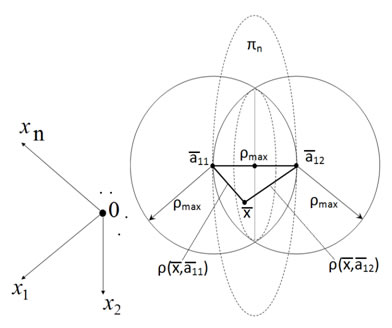
Рис. 1. Возможное местоположение точек множества А
К подмножеству ![]() относим те точки
относим те точки ![]() множества А, которые лежат по одну сторону с его начальной точкой
множества А, которые лежат по одну сторону с его начальной точкой ![]() , в этом случае
, в этом случае ![]() (или
(или ![]() .). К подмножеству
.). К подмножеству![]() относим те точки, которые ближе к
относим те точки, которые ближе к![]() , для них
, для них ![]() (или
(или![]() ).
).
Такой алгоритм разделения прост. Однако при его применении возникает неопределенность в отношении точек, лежащих на граничной плоскости ![]() , у которых
, у которых ![]() (
(![]() ). Также точки, лежащие достаточно близко границе
). Также точки, лежащие достаточно близко границе ![]() , могут быть не оптимально включены в соответствующее подмножество из-за того, что они близки к другому подмножеству.
, могут быть не оптимально включены в соответствующее подмножество из-за того, что они близки к другому подмножеству.
Для контроля подобных ситуаций предложено ввести предельную величину отклонения![]() , которая позволяет априорно выделить:
, которая позволяет априорно выделить:
а) множество точек, гарантированно входящих в оптимальное подмножество ![]() при выполнении условия:
при выполнении условия: ![]() ; (либо
; (либо![]() ) и б) множество точек, гарантированно входящих в оптимальное подмножество
) и б) множество точек, гарантированно входящих в оптимальное подмножество ![]() , для которых выполняется условие:
, для которых выполняется условие: ![]() ; (либо
; (либо![]() ).
).
При введенном априорном пограничном значении ![]() возникает пограничный слой, точки которого удовлетворяют условиям:
возникает пограничный слой, точки которого удовлетворяют условиям:
![]() ;
; ![]() .Для них невозможно сразу же сделать заключение о принадлежности к оптимальным множествам
.Для них невозможно сразу же сделать заключение о принадлежности к оптимальным множествам ![]() и
и ![]() . Рассмотрим оценку возможной величины априорного отклонения
. Рассмотрим оценку возможной величины априорного отклонения ![]() . Максимальные значения данного отклонения достигаются в модельной ситуации, когда:
. Максимальные значения данного отклонения достигаются в модельной ситуации, когда:
- разделяемые точки множества А лежат в одной гиперплоскости (рис.2 а),
- есть две промежуточных группы с центрами ![]() и
и ![]() и довольно большими числами точек N>> 1 на границах возможной области, симметрично расположенные слева и справа относительно крайней точки области
и довольно большими числами точек N>> 1 на границах возможной области, симметрично расположенные слева и справа относительно крайней точки области ![]() , угловые отклонения точек
, угловые отклонения точек ![]() и
и ![]() соответственно от точек
соответственно от точек ![]() и
и ![]() обозначим через
обозначим через ![]() .
.
Перейдем для сокращения обозначений к масштабированным координатам, значения которых разделены на величину ![]() и введем в рассмотренной плоскости вспомогательную систему координат с центром в точке
и введем в рассмотренной плоскости вспомогательную систему координат с центром в точке ![]() и осью х, проходящей через точку
и осью х, проходящей через точку ![]() . В ней координаты точек
. В ней координаты точек ![]() и
и ![]() следующие:
следующие:
![]() .
.
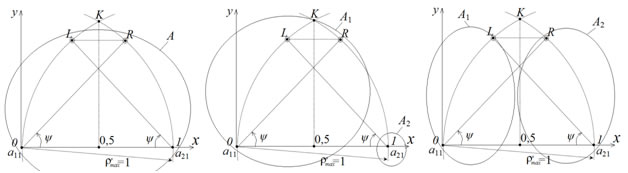
При угле ![]() , близком к
, близком к![]() , и приближении точек
, и приближении точек ![]() и
и ![]() к
к ![]() оптимальным вариантом разбиения будет присоединение обеих промежуточных групп к одной из начальных точек, например, к
оптимальным вариантом разбиения будет присоединение обеих промежуточных групп к одной из начальных точек, например, к ![]() (рис.2 б). В этом случае параметры получаемых множеств
(рис.2 б). В этом случае параметры получаемых множеств ![]() ,
, ![]() и величина критерия будут следующие:
и величина критерия будут следующие:
![]()
![]() ;
;
![]() .
.
При меньшем угле y и более удаленном взаимном расположении точек ![]() и
и ![]() оптимальным вариантом разбиения будет присоединение точки
оптимальным вариантом разбиения будет присоединение точки ![]() к
к ![]() , а
, а![]() к
к ![]() , (рис.2 в). При этом получим следующие параметры множеств
, (рис.2 в). При этом получим следующие параметры множеств ![]() ,
, ![]() и величину критерия:
и величину критерия:
![]() ;
;
![]()
![]()
При пороговом положении точек ![]() и
и ![]() выполняется равенство:
выполняется равенство: ![]() . Отсюда следует условие для порогового значения угла
. Отсюда следует условие для порогового значения угла ![]() :
:
![]()
Перейдем для упрощения вида выражения к новой переменной :
![]()
Условие принимает вид:
![]() .
.
Умножая обе части на знаменатель левой части и возводя обе части в квадрат, получим:
![]() .
.
Перенося все слагаемые в левую части и приводя подобные слагаемые, получим кубическое уравнение относительно ![]() :
:
![]() .
.
Подстановкой несложно проверить, что одним из корней будет значение t= -1. Данное значение на входит в допустимый отрезок [0;4]. Разделив уравнение на (t +1), получим квадратное уравнение относительно ![]() :
:
![]() .
.
Его корни:![]() . Условию
. Условию ![]() удовлетворяет корень
удовлетворяет корень ![]() .
.
Подставляя выражение для t, получим:
![]() .
.
При данном значении угла ![]() . Ему соответствует теоретическое значение предельной величины отклонения
. Ему соответствует теоретическое значение предельной величины отклонения ![]() . Поскольку данная величина найдена для предельных, в действительности не реализуемых вариантов подмножеств точек в А, то для практических расчетов принята величина априорного отклонения
. Поскольку данная величина найдена для предельных, в действительности не реализуемых вариантов подмножеств точек в А, то для практических расчетов принята величина априорного отклонения ![]() = 0,6. При этом условия априорного включения точки
= 0,6. При этом условия априорного включения точки ![]() из множества А в подмножества А1 и А2 имеют вид, соответственно:
из множества А в подмножества А1 и А2 имеют вид, соответственно:
![]() .
.
Данное правило также предложено применить для последующего после априорного расширения подмножеств А1 и А2. Только для тех точек, к которым данное правило уже не применимо, применяется переборный принцип разделения.
Рассмотрим приближенный алгоритм решения задачи.
1. Исходные данные:
1) n - размерность пространства U,
2) nе - число точек в множестве А, (n1≥2),
3) А[1:nе][1:n] - массив координат точек множества А.
2. Решаемые задачи:
1) определение чисел элементов n1, n2 и массивов координат точек в квазиоптимальной паре бинарных подмножеств А1 и А2, у которых значение критерия λ(А1,А2) близко к глобальному максимуму λ max;
2) определение центров тяжести C1,C2 найденных квазиоптимальных бинарных подмножеств А1 и А2.
Приближенный алгоритм бинарной кластеризации (ПАБК).
Шаг 1. Предварительный анализ относительного положения точек А. Построение матрицы расстояний.Определение min и max расстояний. Формирование списка PR[1:P] всех пар максимально удаленных точек. Введение начального значения критерия текущего оптимального разбиения:KR_MIN := 2ρmax.
Шаг 2. Перебор всех P пар максимально удаленных точек. Цикл по параметру s (1≤ s ≤ P) по всем парам максимально удаленных точек.
Шаг 2.1. Начальные присваивания:
а) номера очередных максимально удаленных точек: m1:= PR[s][1]; m2:= PR[s][2];
б) засылка точек m1и m2 в текущие множества А1т и А2т и центры тяжести`С1т и `С2т;
в) формирование начального списка координат точек невключенных вершин AN, а также списков расстояний RC1 и RC2 точек m1и m2 до точек из AN.
Шаг 2.2. Циклическое наращивание текущих множеств А1т и А2т за счет включения в них близких точек. Во внутреннем цикле просмариваются все невключенные точки. Для них определяется соотношение D12=RC1[i]/RC2[i]. Если D12<=0.6, то точка из AN включается в А1т; если D12>=1.67, то точка из AN включается в А2т. Иначе точка остается в множестве AN.Если произошло включение новых точек в множество А1т, то корректируется его центр тяжести`С1т и список расстояний RC1. Аналогично, если произошло включение новых точек в множество А2т, то корректируется его центр тяжести ![]() и список расстояний RC2.
и список расстояний RC2.
Шаг 2.3. Оценка результатов наращивания текущих множеств А1т и А2т за счет включения в них близких точек.
Если все точки из AN включены в А1т и А2т (решение задачт бинарной кластеризации получено), то запись полученных данных и выход из алгоритма.
Если не все точки из AN включены в А1т и А2т , то разделение оставшихся выполняется путем перебора вариантов по аналогии с точным решением.
Завершение работы алгоритма.
Моделирование точного и приближенного алгоритмов производилось на широком наборе множеств. Как правило, результат работы приближенного алгоритма совпадает с разбиением, полученным по точному алгоритму. В специальных модельных случаях значения критерия у приближенного метода хуже, чем у точного примерно на 15 %.
В частности, для модельного множества А ={{0;0}; {1;0};{1;1};{0;1};{0;0,8}; {0,2;1}; {0,25;0,25}; {1,00;0,5}} (рис.3а) в двумерном пространстве признаков точное решение (рис.3 б) дает значение критерия, равное λmax=1.097.
Решение: n1 = 5, А1 = {{1.0,0.0}; {1,00;0,5};{0.0,0.0};{1.0,1.0}; {0.25,0.25};n2 = 3, А2 = {{0.0,1.0},{0.0,0.8},{0.2,1.0}}, полученное по приближенному методу, дает значение критерия λmax=0.930, что на 15% хуже, чем глобально оптимальное значение.
Применение дополнительных операций отсечения и бинарной кластеризации позволяет построить общий алгоритм разделения множеств произвольной структуры со сложным относительным пространственным положением путем построения иерархических нормальных классификаторов соответствующих множеств.
Литература:
- Н.И. Гданский, А.М. Крашенинников. Бинарная кластеризация объектов в многомерных пространствах признаков [Текст] // Труды Социологического конгресса. РГСУ. 2012. – 94-98 с.
- Н.И. Гданский, М.Л. Рысин, А.М. Крашенинников, Линейная классификация объектов с использованием нормальных гиперплоскостей [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 – Режим доступа: http://ivdon.ru/magazine/archive/n4p1y2012/1324 (доступ свободный) - Загл. С экрана. – Яз. рус.
- Н.И. Гданский, А.В. Карпов, А.А. Бугаенко. Оптимальное интерполирование типовых динамик в задаче управления с прогнозированием [Электронный ресурс] // «Инженерный вестник Дона», 2012, №3 – Режим доступа: http://ivdon.ru/magazine/archive/n3y2012/936 (доступ свободный) - Загл. С экрана. – Яз. рус.
- Л. Г. Комарцова, А. В. Максимов. Нейрокомпьютеры // Изд-во МГТУ им. Н.Э. Баумана, 2002. — С. 320.
- Н.И. Гданский, А.М. Крашенинников. Сравнение эффективности методов бинарной кластеризации множество точек-прецендентов [Текст] // Математический методы и приложения: Труды двадцать вторых математических чтений РГСУ. АПКиППРО. 2013. – 59-67 с.
- Л.Н. Ясницкий. Введение в искусственный интеллект. — 1-е. // Издательский центр «Академия», 2005. — С. 176.
- Н.И. Гданский, М.Л. Рысин, А.М. Крашенинников. Применение современных информационных технологий в учебном процессе высшей школы [Текст]: монография // Изд-во РГСУ, 2012, ISBN 978-5-905675-31-7. – С.150.
- Н.И. Гданский, А.М. Крашенинников, Е. А. Слюсарев. Использование геометрического подхода при построении классификаторов в системах искусственного интеллекта [Текст] // Математическое моделирование в проблемах рационального природопользования. Сборник научных трудов Всероссийской молодежной конференции. РГСУ. 2012. – с.36-43.
- Structure of Decision. The Cognitive Maps of Political Elites // Ed. by R. Axelrod. – Princeton: Princeton University Press, 1976. - 405 p.
- Shapiro M.J., Bonham G.M. Cognitive processes and foreign policy decision-making // International Studies Quarterly. 1973. – P. 147–174.