Разработка модели для расчета напряженно-деформированных состояний в полупроводниковых структурах при лазерном воздействии
Аннотация
Дата поступления статьи: 26.05.2014В работе предложена математическая модель, позволяющая рассчитывать термомеханические
напряжения, возникающие в многослойных полупроводниковых структурах при лазерном воз-действии. Разработанное на основе модели программное обеспечение позволяет определить опти-мальные параметры лазерного воздействии с учетом физико-топологических параметров струк-туры. Модель разделена на две задачи: в первой решается нестационарное уравнение теплопро-водности, а во второй уравнения совместимости и обобщенный закон Гука из теории упругости. Для решения уравнений использовался метод конечных разностей.Ключевые слова: Лазерные технологии, термоупругие напряжения, метод конечных разностей
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Текстурирование, рекристаллизация и отжиг при помощи лазеров широко приеняются при создании сенсибилизированных красителем солнечных элементов (СКСЭ), жестких дисков, панелей и прочих полупроводниковых структур, позволяя управлять микрогеометрией поверхности и структурой пленок благодаря локальности термического воздействия [1 – 4]. Во многих случаях лазерный луч фокусируют в полоску, которая сканирует поверхность, а распределение плотности мощности лазера по координате x приводят к прямоугольному виду (рис. 1) [2, 3].
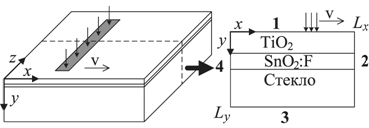
Рис. 1. – Структура СКСЭ, направление осей и нумерация границ
Однако локализация теплового воздействия приводит к большим градиентам температур в зоне воздействия лазерного луча, большим термомеханическим напряжениям и появлению дефектов. Это особенно актуально в случае с многослойными структурами, в которых пленки имеют различные термические и механические параметры, основным из которых в данном случае является коэффициент линейного расширения. Проведение экспериментальных исследований напряженно-деформированных состояний в зоне воздействия лазерного луча вызывает определенные трудности.
В настоящее время широко применяется математическое моделирование, в частности, численные методы, которые позволяют проводить численные эксперименты и определять оптимальные параметры и режимы [3-9].
Задачу нахождения термомеханических напряжений при воздействии лазерного излучения можно разделить на две независимые:
– нахождение распределения температуры при воздействии лазерного излучения;
– нахождение механических напряжений и смещений под воздействием температурного поля.
Моделированию распределения температуры при лазерном воздействии посвящено множество работ. Однако в большинстве случаев вводят допущение о том, что лазерное излучение полностью поглощается верхним слоем [4, 6, 7]. В случае со структурой СКСЭ на основе пористого оксида титана, в которой толщины пленок составляют менее 10 мкм [1], а подложкой является стекло прозрачное для длины волны 1064 нм, это допущение не может быть использовано. Именно поэтому, необходимо использовать модель серого тела и учитывать оптические свойства всех слоев, входящих в структуру, для расчета плотности мощности поглощенного лазерного излучения [2, 3, 8].
Термоупругие напряжения, возникающие при лазерной обработке, сильно зависят от формы лазерного луча и режима воздействия, а так же от физико-топологических параметров обрабатываемой структуры. При нахождении напряжений в большинстве случаев используют двумерную модель плоского напряженного состояния [7, 9, 10]. В работе [9] напряжения рассматривались для плоскости xz (см. рис. 1), что определялось задачей, а в работах [7, 10, 11], рассматривались напряжения в плоскости xy (см. рис. 1), но задача решалась в цилиндрической системе координат, поскольку форма сечения сфокусированного луча была круглой, и луч не перемещался по поверхности структуры.
Поэтому необходима модель, позволяющая учитывать процесс сканирования подложки лазерным лучом с учетом формы сфокусированного пятна и многослойности обрабатываемой структуры.
Задачу нахождения термомеханических напряжений при воздействии лазерного излучения для данного случая можно упростить до двумерной, поскольку длина сечения лазерного луча по координате z много больше размера по x (рис. 1).
Для расчета температурного поля было использовано нестационарное двумерное уравнение теплопроводности, которое в декартовой системе координат буде иметь следующий вид:
![]() , (1)
, (1)
где с – удельная теплопроводность; ![]() – плотность; Т – температура в структуре; t – время;
– плотность; Т – температура в структуре; t – время; ![]() – коэффициент теплопроводности; q – плотность мощности источника тепла.
– коэффициент теплопроводности; q – плотность мощности источника тепла.
Источником тепла является лазерное излучение. Количество энергии лазерного излучения поглощенное серым телом может быть описано выражением Бугера-Ламберта-Бера:
![]() , (2)
, (2)
где R – коэффициент отражения; a – коэффициент поглощения; I0 – плотность мощности лазерного излучения.
Для задачи термоупругости, в случае, представленном на рис. 1, вводятся следующие допущения: в направление оси z не может быть смещения и все компоненты деформации будут функциями только от x и y, поскольку по данной координате задача является протяженной. Данная задача сводится к двумерной задачи плоской деформации [12], для которой уравнения равновесия примут вид:
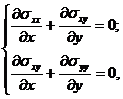 (3)
(3)
где σxx, σxy, σyy – компоненты тензора напряжения.
Поскольку задача будет решаться в напряжениях, необходимо использовать уравнения совместимости [12], которые в данном случае будут сведены к следующему выражению:
![]() , (4)
, (4)
где ex, ey – продольная деформация; gxy – деформация сдвига.
Обобщенный закон Гука с учетом теплового расширения тела и вышеперечисленных допущений будет следующим:
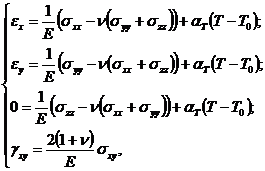 (5)
(5)
где E – модуль Юнга; αT – коэффициент линейного теплового расширения; T0 – начальная температура тела.
Подставив выражение (5) в (4) и выразив напряжения σzz через σxx и σyy, с учетом уравнений равновесия (3) получим следующую систему дифференциальных уравнений:
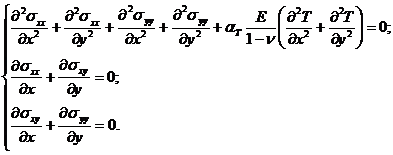 (6)
(6)
Использование уравнений 1-го порядка при дискретизации недопустимо, т.к. это приводит к неадекватным результатам [9].
Продифференцируем поxвторое уравнения системы (6) и третье уравнение поy, а затем вычтем из второго уравнения третье, а так же продифференцируем поyвторое уравнения системы (6) и третье уравнение поx, а затем сложим оба уравнения, получим следующую систему:
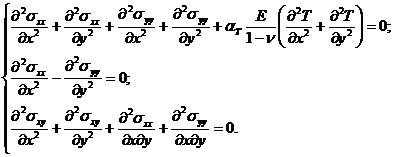 (7)
(7)
Начальное условие для уравнения теплопроводности (1) имеет вид:
![]() (8)
(8)
На всех гранях была задана свободная конвекция, которая описывается граничными условиями второго рода:
![]() , (9)
, (9)
где n – нормаль к грани; α – коэффициент конвективного теплообмена.
Граничные условия для системы (7) могут быть описаны при помощи уравнений равновесия, которые с учетом отсутствия механических воздействий для данной задачи будут иметь следующий вид [12]:
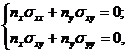
где nx, ny – компоненты нормали к поверхности.
Подставляя соответствующие компоненты нормалей каждой грани, получим следующие граничные условия:
– для первого уравнения системы (7) на 1 и 3 гранях (см. рис. 1) ![]() ;
;
– для второго уравнения системы (7) на 2 и 4 гранях (см. рис. 1) ![]() ;
;
– для третьего уравнения системы (7) на всех гранях (см. рис. 1) ![]() .
.
Недостающие граничные условия для первого и второго уравнений системы (7) будут следующими: на 2 и 4 гранях ![]() , а на 1 и 3 -
, а на 1 и 3 - ![]() .
.
Заключение
В работе представлена модель, позволяющая рассчитать распределение напряжения в полупроводниковой структуре под действием сканирующего лазерного излучения. Для решения системы, состоящей из уравнений (1), (2), (7) с соответствующими граничными условиями был использован метод конечных разностей. Для решения уравнения теплопроводности использовалась неявная схема. Для решения первых двух уравнений системы (7) использовался итерационный алгоритм. Что позволяет моделировать многослойные структуры с различными физическими и топологическими параметрами слоев, варьировать скорость сканирования и мощность лазерного луча. В модели, так же, внесены допущение о неизменности физических параметров слоев под действием температуры.
Работа выполнена при финансовой поддержке Министерства образования и науки России (уникальный системный номер заявки – 2014-14-576-0055-1063 в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014-2020 годы»).
Литература:
- Малюков С.П., Саенко А.В., Рукавишникова А.С., Куликова И.В., Теоретическое исследование влияния толщины и структуры электрода TiO2 на фотоэлектрические характеристики солнечного элемента [Текст] // Известия ЮФУ. Технические науки. 2012. – № 1. С. 63-71.
- Малюков С.П., Куликова И.В., Калашников Г.В., Приступчик Н.К. Исследование влияния режимов работы Nd:YAG лазера на напряженно-деформированные состояния в обрабатываемой полупроводниковой структуре [Электронный ресурс] // «Инженерный вестник дона», 2013, № 4 Режим доступа: http://www.ivdon.ru/magazine/archive/n4y2013/2000 (доступ свободный) – Загл. с экрана. – Яз. Рус.
- С.П. Малюков, И.В. Куликова, Калашников Г.В. Моделирование процесса лазерного отжига структуры «кремний-стекловидный диэлектрик» [Текст] // Известия ЮФУ. Технические науки. 2011. – № 7. – С. 182-188.
- Shakeel Safdar, Lin Li, M.A. Sheikh, Zhu Liu. Finite element simulation of laser tube bending: Effect of scanning schemes on bending angle, istortions and stress distribution [Text] // Optics & Laser Technology 39 (2007) pp. 1101 – 1110.
- Малюков С.П., Куликова И.В., Петерс С.И.. Разработка модели взаимодействия лазерного излучения с биологическими тканями [Электронный ресурс] // «Инженерный вестник дона», 2013, № 4 Режим доступа: http://www.ivdon.ru/magazine/archive/n4y2013/1999 (доступ свободный) – Загл. с экрана. – Яз. Рус.
- M. Mamat, N. Tofany, A. Kartono. Numerical Analysis of Heat Conduction and Phase Transformation in Laser Transformation Hardening: Influences of Heating Duration and Laser Beam Intensity [Text] // Applied Mathematical Sciences, Vol. 4, 2010, no. 61, pp. 3019 – 3033.
- В.И. Мажукин, B.B. Hocoe, U.Semmler. Исследование тепловых и термоупругих полей в полупроводниках при импульсной обработке [Текст] // Матем. моделирование, 12:2 (2000). – С. 75–83.
- Малюков С.П., Куликова И.В. Бростилов С.А. Моделирование теплового воздействия лазерного излучения на биологические ткани [Текст] // Фундаментальные исследования. Часть 2, 2012. – № 11. – С. 425-429.
- Рындин Е.А., Рыжук Р.В., Исаева А.С. Математическая модель механических напряжений, инициированных лазерным импульсом [Текст] // Фундаментальные исследования, 2012. – №.11. – С.609 - 614
- W.-S. Kim, L. G. Hector, R. B. Hetnarski. Thermoelastie stresses in a bonded layer due to repetitively pulsed laser radiation [Text] // Acta Mechanica 125, (1997). Springer-Verlag, pp. 107-128
- B. S. Yilbas & N. Ageeli (2006) Thermal Stress Development Due to Laser Step Input Pulse Heating [Text] // Journal of Thermal Stresses, 29:8, pp. 721-751 To link to this article: http://dx.doi.org/10.1080/01495730600705349
- Ван Цза-Де. Прикладная теория упругости [Текст] // – М: Изд-во Физ.-мат. лит., 1959. – 406 с.