Модификация расчета матрицы обратной связи по состоянию для линейных многомерных объектов
Аннотация
В данной статье предлагается методика расчёта матрицы обратной связи по вектору координат состояния. В её основу положено объединение двух задач. Первой является задача компенсации нулей собственных и взаимных передаточных функций системы, второй – задача обеспечения монотонности протекания процессов в системе. Также могут быть решёны задачи такие как: задача развязывания и задача обеспечения астатизма каналов управления. Под модификацией понимается получение соотношения в общем виде для матрицы регулятора обратной связи системы модального управления. Полученная система обеспечивает монотонность переходной характеристики за счет компенсации множества нулей собственных и взаимных передаточных функций в системе модального управления. С технологической точки зрения система обеспечивает отсутствие перерегулирования при протекании технологического процесса. Предложенные решения в предлагаемой статье могут быть использованы в различных областях науки и техники.
Ключевые слова: модальное управление, компенсация нулей, модификация алгоритма расчёта обратной связи, монотонность переходной характеристики
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
1. Введение. Современные технологические процессы предъявляют сегодня повышенные требования к качеству систем автоматического управления [11, 12], на которые возлагаются всё более ответственные функции. В специальной литературе по теории автоматического управления важное место занимают работы, посвящённые синтезу многоканальных систем управления, а в частности, синтезу − систем управления по модальной методике. Наиболее распространены системы с модальным управлением (СМУ) [1 – 10] как для одномерных, так и для многомерных объектов управления. Однако в СМУ матрица обратной связи по состоянию (ОСС) удовлетворяет лишь одному требованию – размещению корней характеристического уравнения (известна как «задача об управлении спектром полюсов» [2]). Остальные требования, предъявляемые к системе управления, игнорируются при расчете матрицы ОСС многомерной системы. В системах модального управления до конца не решен вопрос о компенсации нулей собственных и взаимных передаточных функций [3]. В отечественной и зарубежной литературе методам компенсации таких нулей и управления ими уделено мало внимания применительно к СМУ [1, 2, 9]. Не скомпенсированные нули искажают результирующую переходную характеристику системы управления [9]. Избежать подобных недостатков позволяют различного рода модификации алгоритма вычисления матрицы ОСС, в которых выше упомянутые нули передаточных функций скомпенсированы без ухудшения остальных показателей качества системы управления.
2. Постановка задачи. Рассмотрим многосвязный полностью управляемый и наблюдаемый объект управления (ОУ) с равным числом входов и выходов, описываемый системой уравнений в пространстве состояний
![]() (1)
(1)
где ![]() – n-мерный вектор координат состояния,
– n-мерный вектор координат состояния, ![]() – m-мерный вектор управляющих воздействий,
– m-мерный вектор управляющих воздействий, ![]() – m-мерный вектор выходных переменных, n ≥ m,
– m-мерный вектор выходных переменных, n ≥ m, ![]() –собственная матрица объекта,
–собственная матрица объекта, ![]() –матрица управлений,
–матрица управлений, ![]() ‒матрица выхода;
‒матрица выхода; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Предполагается, что вектор координат состояния
. Предполагается, что вектор координат состояния ![]() полностью доступен прямому измерению. Пусть для объекта (1) обратная связь по состоянию представима в виде
полностью доступен прямому измерению. Пусть для объекта (1) обратная связь по состоянию представима в виде
![]() , (2)
, (2)
где ![]() – матрица ОСС,
– матрица ОСС, ![]() , а
, а ![]() – m-мерный вектор входа СМУ.
– m-мерный вектор входа СМУ.
Задача нахождения матрицы ![]() в законе управления (2), для многомерного случая имеет неединственное решение [1, 6, 7], при этом могут быть предложены различные алгоритмы её вычисления.
в законе управления (2), для многомерного случая имеет неединственное решение [1, 6, 7], при этом могут быть предложены различные алгоритмы её вычисления.
Рассмотрим передаточную матрицу (ПМ) для объекта управления, описанного системой (1), замкнутого обратной связью (2). В её состав входит ![]() передаточных функций (собственных и взаимных передаточных функций). Потребуем, чтобы множества их нулей совпадало с множеством полюсов. В результате чего нули ПМ будут «скомпенсированными» для СМУ. Полюса зададим совпадающими и лежащими в точке Ω, см. рис. 1, на левой действительной оси комплексной плоскости, чтобы обеспечить монотонность переходной характеристики.
передаточных функций (собственных и взаимных передаточных функций). Потребуем, чтобы множества их нулей совпадало с множеством полюсов. В результате чего нули ПМ будут «скомпенсированными» для СМУ. Полюса зададим совпадающими и лежащими в точке Ω, см. рис. 1, на левой действительной оси комплексной плоскости, чтобы обеспечить монотонность переходной характеристики.
Классическая процедура расчёта матрицы ![]() , в законе (2), подразумевает нахождения матрицы преобразования от исходного базиса модели (1), к заданному базису [6, 7]. Потребуем, чтобы имелась возможность вычисления матрицы ОСС, в законе (2), через матрицы
, в законе (2), подразумевает нахождения матрицы преобразования от исходного базиса модели (1), к заданному базису [6, 7]. Потребуем, чтобы имелась возможность вычисления матрицы ОСС, в законе (2), через матрицы ![]() ,
, ![]() ,
, ![]() объекта (1), т. е. в исходном базисе, для упрощения процедуры реализации полученного соотношения, для матрицы
объекта (1), т. е. в исходном базисе, для упрощения процедуры реализации полученного соотношения, для матрицы ![]() , на ЭВМ.
, на ЭВМ.
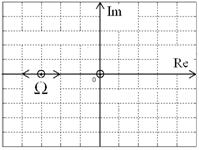
Рис. 1. Спектр полюсов СМУ
3. Метод решения. Представим уравнение выхода в модели (1), как ![]() и его производную
и его производную ![]() , где
, где ![]() − i-я компонента вектора выхода,
− i-я компонента вектора выхода, ![]()
![]() -я строка,
-я строка, ![]() , матрицы выхода,
, матрицы выхода, ![]() ,
, ![]() ‒ единичная матрица,
‒ единичная матрица, ![]() . Замкнем ОУ, описанный системой уравнений (1), обратной связью (2), имеем
. Замкнем ОУ, описанный системой уравнений (1), обратной связью (2), имеем
![]() . (3)
. (3)
В (3) индекс ji назовём «минимальным индексом произведения матриц». Который является целым положительным числом, ![]() . Потребуем, чтобы матрица
. Потребуем, чтобы матрица ![]() относительно вектора входа, в (3), давала не нулевую блочную строку для ji [5].
относительно вектора входа, в (3), давала не нулевую блочную строку для ji [5].
Запишем теорему Келли-Гамильтона для ОУ (1) замкнутого ОС (2) и помножим её справа на ![]() -ю вектор-строку, получим
-ю вектор-строку, получим
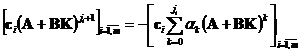 ,
,
Учитывая полученное выражение перепишем дифференциальные уравнения, представленные выражением (3)
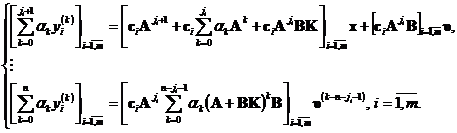 (4)
(4)
где ![]() – коэффициенты, величина которых неизвестна и может быть задана при синтезе СМУ. Коэффициенты
– коэффициенты, величина которых неизвестна и может быть задана при синтезе СМУ. Коэффициенты ![]() будем задавать для биномиального разложения, тогда переходные процессы на выходе системы управления будут носить монотонный характер и свидетельствовать о подавлении действия нулей собственных и взаимных передаточных функций СМУ:
будем задавать для биномиального разложения, тогда переходные процессы на выходе системы управления будут носить монотонный характер и свидетельствовать о подавлении действия нулей собственных и взаимных передаточных функций СМУ:
![]() ,
, ![]() ,
,
где ![]() ‒биномиальные коэффициенты (могут быть определены по «схеме треугольника Паскаля»), Ω‒ среднегеометрический корень,
‒биномиальные коэффициенты (могут быть определены по «схеме треугольника Паскаля»), Ω‒ среднегеометрический корень, ![]() , определяющий быстродействие
, определяющий быстродействие ![]() в синтезируемой системе [6].
в синтезируемой системе [6].
Для нахождения матрицы обратной связи ![]() в законе управления (2) будем рассматривать выражение для матриц относительно вектора
в законе управления (2) будем рассматривать выражение для матриц относительно вектора ![]() в (4), имеем:
в (4), имеем:
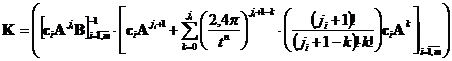 . (5)
. (5)
В результате получено соотношение для матрицы обратной связи, которое вычисляется, напрямую через матрицы ![]() ,
, ![]() ,
, ![]() объекта (1), представленного в пространстве состояний в исходном базисе. По соотношению (5) матрица
объекта (1), представленного в пространстве состояний в исходном базисе. По соотношению (5) матрица ![]() в законе управления (2) может быть «легко» вычислена при помощи ЭВМ [10].
в законе управления (2) может быть «легко» вычислена при помощи ЭВМ [10].
Остаётся открытым вопрос – для какого класса объектов управления, вида (1) выражения (5) может быть вычислено? Для этого будем рассматривать передаточную матрицу СМУ ‒![]() , учитывая (4):
, учитывая (4):
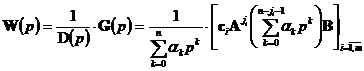 , (6)
, (6)
где ![]() ‒матричный полином СМУ, m×m-мерная полиномиальная матрица,
‒матричный полином СМУ, m×m-мерная полиномиальная матрица, ![]() ‒характеристический полином СМУ,
‒характеристический полином СМУ, ![]() . Из правой части выражения (6) видно, что нули собственных и взаимных передаточных функций и полюса являются сократимыми. При этом число полюсов, по i-й строке ПМ равно
. Из правой части выражения (6) видно, что нули собственных и взаимных передаточных функций и полюса являются сократимыми. При этом число полюсов, по i-й строке ПМ равно ![]() ,
, ![]() .
.
Рассматривая методику вычисления полного множества нулей (см. например [10]) для управляемого, наблюдаемого ОУ (1), имеющего равное число входов и выходов, имеем:
![]() . (7)
. (7)
В выражении (11) ![]() ‒нулевой полином,
‒нулевой полином, ![]() , который может быть найден, как определитель матрицы Розенброка [8],
, который может быть найден, как определитель матрицы Розенброка [8], ![]() ‒число нулей (1) [8]. Учитывая (7) и выше введённые обозначения:
‒число нулей (1) [8]. Учитывая (7) и выше введённые обозначения: ![]() ,
, ![]() для (6), можно записать «тождество конечных нулей»:
для (6), можно записать «тождество конечных нулей»:
![]() . (8)
. (8)
Перепишем тождество (8), рассматривая любую i-ю строку для матричного полинома:
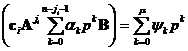 . (9)
. (9)
Выражение (9) является эквивалентом скалярной системы. Далее будем рассматривать порядки полиномом в левой и правой частях выражения (9). Всего таких полиномов в системе m штук:
![]() , (10)
, (10)
Если ОУ вида (1) является управляемым и наблюдаемым и имеет µ нулей при этом число «свободных» полюсов ![]() в
в ![]() раз меньше. В результате µ полюсов не подлежат сдвигу и являются инвариантными относительно ОСС. Поэтому целесообразно выбирать такой класс ОУ вида (1) для которого µ = 0. При этом все полюса системы с ОСС и матрицей (5) будут свободными и могут быть помещены в заданную точку Ω на комплексной плоскости. Из выражения (7) видно, что если матрица Розенброка является унимодальной, то степень полинома
раз меньше. В результате µ полюсов не подлежат сдвигу и являются инвариантными относительно ОСС. Поэтому целесообразно выбирать такой класс ОУ вида (1) для которого µ = 0. При этом все полюса системы с ОСС и матрицей (5) будут свободными и могут быть помещены в заданную точку Ω на комплексной плоскости. Из выражения (7) видно, что если матрица Розенброка является унимодальной, то степень полинома ![]() равна нулю (µ = 0). Наличие унимодальной матрицы Розенброка свидетельствует об отсутствии развязанных нулей, т. е. СМУ не имеет неуправляемых и ненаблюдаемых подсистем. Выражение (10) окончательно определяет класс рассматриваемых объектов, вида (1), для которого может быть найдено выражение (5).
равна нулю (µ = 0). Наличие унимодальной матрицы Розенброка свидетельствует об отсутствии развязанных нулей, т. е. СМУ не имеет неуправляемых и ненаблюдаемых подсистем. Выражение (10) окончательно определяет класс рассматриваемых объектов, вида (1), для которого может быть найдено выражение (5).
На завершающем этапе алгоритма расчёта матрицы обратной связи по состоянию можно предложить блок-схему см. рис. 2, в общем виде [10].
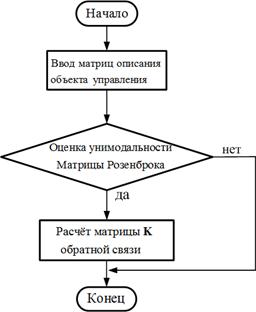
Рис.2. Блок-схема алгоритма расчёта обратной связи по состоянию
На первом этапе производим ввод матриц объекта управления, согласно модели (1). На втором этапе производится оценка унимодальности матрицы Розенброка для (1). На третьем этапе выполняется расчёт матрицы ![]() ОСС по выражению (5) и выход из алгоритма расчета.
ОСС по выражению (5) и выход из алгоритма расчета.
4. Описание существующих компенсационных подходов для СМУ.
Основным требованием при синтезе системы с применением компенсационного подхода является получение заданного вида матричного полинома СМУ. Так как в этом случае нули собственных и взаимных передаточных функций являются скомпенсированными. Матричный полином системы модального управления должен при этом вырождаться в числовую матрицу ![]() ,
, ![]()
![]() ,
,
где ![]() −передаточная матрица динамического компенсатора, включаемого на вход СМУ. Единственным ограничением является требование обратимости к СМУ. В результате, поставленная задача синтеза разрешима, если для матричного полинома существует обратная матрица:
−передаточная матрица динамического компенсатора, включаемого на вход СМУ. Единственным ограничением является требование обратимости к СМУ. В результате, поставленная задача синтеза разрешима, если для матричного полинома существует обратная матрица:
![]() .
.
Синтез динамического компенсатора в данном случае может производиться, как рекомендовано в [13]. В этом случае для решения поставленной задачи необходимо последовательно с СМУ включить динамический компенсатор n−го порядка, т. е. соизмеримого с порядком ОУ, что является экономически неэффективным.
Вторым недостатком изложенного компенсационного подхода, является следующее − ![]() n ﴾m−1) элементов матрицы ОСС являются «свободными», т. к. требований к ним, в рамках компенсационного подхода, не предъявляется.
n ﴾m−1) элементов матрицы ОСС являются «свободными», т. к. требований к ним, в рамках компенсационного подхода, не предъявляется.
Выше изложенный компенсационный подход является хорошо применимым при синтезе скалярных систем управления. Так как в этом случае матрица ОСС имеет всего лишь ![]() элементов, которые могут быть с успехом вычислены при решении задачи обеспечения заданного спектра полюсов скалярной системы.
элементов, которые могут быть с успехом вычислены при решении задачи обеспечения заданного спектра полюсов скалярной системы.
Таким образом, при обеспечении компенсации нулей собственных и взаимных передаточных функций, требуется прибегать к «аппаратным затратам» на дополнительное оборудование, что не всегда является экономически приемлемым. Методика расчёта матрицы ОСС вида (5), рассмотренная выше, не требует наличия дополнительного оборудования. При этом требуется лишь провести проверку на соответствие классу рассматриваемых объектов управления по выражению (7) при µ = 0.
Выводы. Рассмотренная методика синтеза ОСС для многомерных ОУ позволяет помещать полюса в заданную точку ![]() на левой действительной оси комплексной плоскости. При этом вид переходной характеристики определяется совокупностью «желаемых» полюсов и не зависит от действия нулей собственных и взаимных передаточных функций, так как методика подразумевает их компенсацию. Это обстоятельство обеспечивает монотонность переходной характеристики на выходе СМУ порождаемую биномиальным разложением.
на левой действительной оси комплексной плоскости. При этом вид переходной характеристики определяется совокупностью «желаемых» полюсов и не зависит от действия нулей собственных и взаимных передаточных функций, так как методика подразумевает их компенсацию. Это обстоятельство обеспечивает монотонность переходной характеристики на выходе СМУ порождаемую биномиальным разложением.
Преимущества данной методики заключаются в том, что она не требует вычисления матрицы перехода к канонической форме управляемости и построения ОУ в «новом базисе», как рекомендуется при классическом подходе к решению данной задачи [7]. Матрица обратной связи по вектору координат состояния вычисляется напрямую через матрицы ![]() ,
, ![]() ,
, ![]() объекта (1), представленного в пространстве состояний в исходном базисе.
объекта (1), представленного в пространстве состояний в исходном базисе.
Апробация выше изложенного алгоритма расчёта заключалась в составлении программного кода на языке MATLAB для расчета произвольных ОУ с равным числом входов и выходов [10]. При этом переходные характеристики всех тестируемых объектов, замкнутых ОСС, имели монотонный характер протекания. Это обстоятельство превосходит существующий ранее классический подход к решению данной задачи.
Список литературы:
- 1.Андреев Ю. Н. Алгебраические методы пространства состоянии в теории управления линейными объектами / Ю. Н. Андреев // АиТ. – 1977. – № 3. – С. 5–49.
2.Борковская И. М. Модальное управление системами с распределенным запаздыванием / И. М. Борковская, В. М. Марченко // АиТ. – 1993. – № 8. – С. 40–52.
3.Воронов А. А. Синтез минимальных модальных регуляторов, действующих от измеримых входа и выхода линейного объекта / А. А. Воронов // АиТ. – 1993. – № 2. – С. 34–51.
4.Губарев В. Ф. Модальный анализ и синтез управления в системах с неизвестной априори моделью / В. Ф. Губарев // Теория и системы управления. – 2003. – № 2. – С. 20–33.
5.Кревенцов Е. Г. Компенсация множества конечных нулей многомерных объектов с равным числом входов и выходов при синтезе модальным методом / Е. Г. Кревенцов // Актуальные проблемы электронного приборостроения. – Новосибирск : Изд-во НГТУ, 2008. – Т. 7. – С. 178–181.
6.Кузовков Н. Т. Модальное управление и наблюдающие устройства / Н. Т. Кузовков. – М.: Машиностроение, 1976. – 112 с.
7.Методы классической и современной теории автоматического управления / К. А. Пупков, Н. Д. Егупов. – М.: МГТУ им. Н. Э. Баумана, 2004. – Т.1. – 400 с.
8. Смагина Е. М. Вопросы анализа линейных многомерных объектов с использованием понятия нуля системы / Е. М. Смагина ; Томск. гос. ун–т. – Томск, 1990. – 160 с.
9.Суровцев В. Н. Теория автоматического управления: учеб. пособие / В. Н. Суровцев, Н. В. Донской. – Чебоксары, Изд-во Чуваш. ун-та, 2005. – 184 с.
10.А. с. О государственной регистрации программы для ЭВМ. Программа расчета астатической САЦ с матричным регулятором в обратной связи по вектору координат состояния / Е. Г. Кревенцов (Россия). - № 2011614126 ; заявл. 10.02.2011 ; опубл. 26.05.2011.
11.Фиговский О. Новейшие нанотехнологии (обзор) / О. Фиговский // Инженерный вестник Дона – 2012. – № 1.
12.Фиговский О. Обзор новейших западных нанотехнологий / О. Фиговский // Инженерный вестник Дона – 2012. – № 2.
13.Целигорова E. H. Современные информационные технологии и их использование для исследования систем автоматического управления / E. H. Целигорова // Инженерный вестник Дона – 2010. – № 3.